机器学习: 贝叶斯决策 1

Bayes rules

在介绍Bayes决策论之前，我们先介绍有关概率的两个基本准则：求和准则与相乘准则。

给定两个随机变量X,Y,假设X可以为任意值xi,其中i=1,2,...M, 同样的,Y可以取的值为yj,其中j=1,2,...L,假设我们对这两个随机变量的所有可能的值进行采样,一共做了N次采样，我们假设这N次采样中，X=xi, Y=yj的样本出现的个数为nij, X取值为xi(不管Y取何值)的样本出现的个数为ci,而Y取值为yj(不管X取何值)的样本出现的个数为rj。

我们可以定义，X取值为xi并且Y取值为yj的概率为p(X=xi,Y=yj),这个称为联合概率,可以通过如下的表达式得到：

p(X=xi,Y=yj)=nijN

同样地，X取值为xi(不管Y取何值)的概率为p(X=xi),其概率表达式为：

p(X=xi)=ciN

我们很容易可以得出ci=∑jnij,相当于将随机变量X的取值固定为xi，然后将所有包含xi的(X,Y)的样本个数进行相加。因此，综上我们可以得到：

p(X=xi)=∑j=1Lp(X=xi,Y=yj)

这就是概率的求和准则,一般我们把p(X=xi)称为边缘概率。

如果我们想考虑所有包含X=xi的(X,Y)的样本中，Y=yj的样本所占的比重,可以表示成p(Y=yj|X=xi),这个称为Y=yj关于X=xi的条件概率，可以由如下的表达式得到：

p(Y=yj|X=xi)=nijci

综合以上的式子，我们可以得到联合概率p(X=xi,Y=yj) 为：

p(X=xi,Y=yj)=nijN=nijci⋅ciN=p(Y=yj|X=xi)p(X=xi)

这个称为概率的相乘准则.

这两个准则可以概括如下：

P(X)=∑YP(X,Y)P(X,Y)=P(Y|X)P(X)

这两个准则是机器学习中概率分析机制的基础。

最后介绍一下Bayes定理，因为P(X,Y)=P(Y,X),由相乘准则我们可以得到如下的表达式：

P(X)P(Y|X)=P(Y)P(X|Y)P(Y|X)=P(Y)P(X|Y)P(X)(Bayes 定理)

利用求和准则，我们可以将定理中的分母表示成：

P(X)=∑YP(X|Y)P(Y)

从某种角度来看，我们也可以将分母P(X)看成一个归一化常数，以保证条件概率P(Y|X)关于Y的所有可能取值的概率和为1.

Two Class Cases

机器学习或者模式识别中，一个常见的挑战就是分类，将一个样本特征x进行分类，当然一个直观的方法就是求出这个样本属于某一类的概率，即P(wi|x),这个概率称为posterior(后验)概率，而Bayes估计就是利用概率进行分类的基础。

我们先考虑两类的情况，假设w1, w2分别表示第一类和第二类，P(w1),P(w2)表示每一类的priori(先验)概率，这个可以由训练样本的统计得到，P(w1)≈N1/N, P(w2)≈N2/N, 另外我们还需要知道每一类的条件概率密度函数p(x|wi),i=1,2,这个函数可以描述每一类的样本分布，这个函数也可以叫做wi关于样本特征x的似然函数(likelihood function),这里一个隐含的假设就是特征x可以取任意值，如果x只能取有限值，那么概率密度函数就变为概率估计，写作P(x|wi).

根据前面介绍的Bayes准则，我们有：

P(wi|x)=p(x|wi)P(wi)p(x)

其中p(x)=∑2i=1p(x|wi)P(wi),很明显,利用Bayes概率来进行分类,只要比较P(w1|x)和P(w2|x)的大小,哪一类的后验概率更大，则该样本就属于哪一类。因为p(x)对于两类来说是一样的，相当于一个归一化常数，所以我们可以只比较p(x|w1)P(w1)与p(x|w2)P(w2)的大小，为了简化问题，假设两类的先验概率一样，即P(w1)=P(w2)=0.5,那么，进一步，我们可以只要考虑p(x|w1)与p(x|w2),所以，这个分类问题，最终演化成比较两类的条件概率密度函数在样本特征取值为x时的大小，

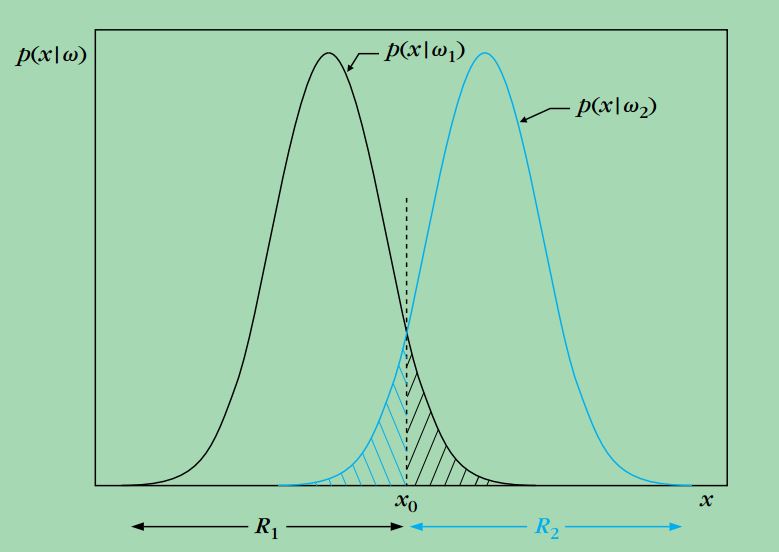
上图给出了在同样的先验概率下，两类的条件概率密度函数的形状，这里的样本特征是一维的，其中穿过x0的虚线表示一个阈值，将样本特征空间分成两个区域R1,R2,根据Bayes决定准则，样本特征落在区域R1则该样本属于w1,如果样本特征落在
区域R2则该样本属于w2,我们可以看到，有些决策错误是无法避免的，比如本应该属于w1的样本特征，落在了区域R2,
因此被划为w2,同样地，属于w2的样本特征，落在了区域R1,因此被划为w1,我们可以用Pe表示错分的概率，其表达式如下：

Pe=12∫x0−∞p(x|w2)dx+12∫∞x0p(x|w2)dx

可以看出，Pe相当于上图中阴影部分的面积，这个表达式其实给出了Bayes概率估计中非常重要的一个评价，我们最初是通过直观的经验来建立分类准则，即将样本划分给最有可能的那一类，我们接下来要证明，这个简单的分类准则有着非常完备的数学解释。

参考文献
Sergios Theodoridis, Konstantinos Koutroumbas, “Pattern Recognition”, 4th edition, 2008, Elsevier.
Christopher M. Bishop, “Pattern Recognition and Machine Learning”, Springer, 2006.