Dapp混合模型开发--Dice2win的解读

前言:
　　之前讲到Dapp原生态对随机函数的支持并不友好, 现在讲讲一种解决思路. 既能保证随机函数的不可预测性, 又能保证公平性, 平台和玩家都能满意. 而Dapp中的Dice2Win实现, 刚好是其中的一个经典例子.

案例:
　　在讲具体的思路前, 来讲一下一个经典的案例:
　　两人分一个苹果, 切成两半分, 不过两人足够理性且追求自身利益的最大化, 请问有什么策略保证最大的公平性呢?
　　猜拳定胜负, 然后由胜利者主导分苹果吗? 哈哈, 这个答案显然不合适.
　　说起这个例子来, 笔者印象也很深, 好想是央视有个节目李开复出的题, ^_^, 也不小心暴露了年龄.
　　答案是: 让一个人来切苹果, 然后让另一个人先挑.
　　先挑的人, 总是能获取最好的半个苹果, 而切苹果为了不让自己利益受损, 它会尽量保证苹果公平的被切开.
　　从这个案例中, 我们或许能得到一些启示, 所谓的公平, 没有所谓先发优势, 只有纳什均衡的平衡点.

思路:
　　Dice2Win的思路和上述的例子类似, 它采用混合模式, 巧妙地解决随机数弱, 且容易被预测的问题. 其整个流程如下:
　　
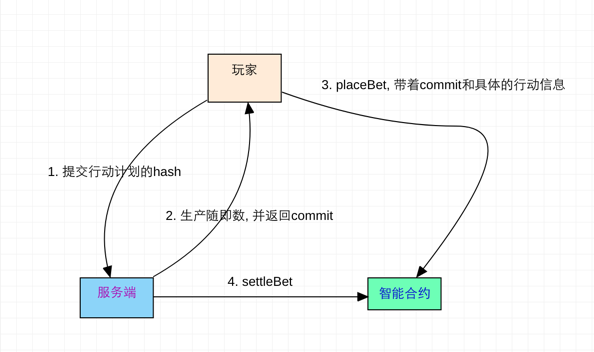
　　1. 玩家指定行动计划, 并生产对应的hash值.
　　2. 服务端收到玩家的hash值, 产生随机值reveal, 然后根据reveal生产commit值, 把这个返回给玩家
　　3. 玩家带着commit和行动信息, 在智能合约下真正下注
　　4. 服务端发起结算, 带着真正的reveal值去结算
　　中间的行动计划和reveal没法中途修改, 因为有hash值的验证
　　其本质的思想是hash-commit-reveal, 其核心的思想是: 服务端不知道玩家的行为, 玩家不知道服务端真正的随机数. 而最终结果在合约里验证hash, 并给出预期的结果. 这样的流程, 保证玩家和服务端都满意.

代码:
　　具体的Dice2Win代码在这, 我们来简单解读一下.
　　placeBet代码片段:

function placeBet(uint betMask, uint modulo, uint commitLastBlock, uint commit, bytes32 r, bytes32 s) external payable {

    Bet storage bet = bets[commit];
    require (bet.gambler == address(0), "Bet should be in a 'clean' state.");

    // Validate input data ranges.
    uint amount = msg.value;
    require (modulo > 1 && modulo <= MAX_MODULO, "Modulo should be within range.");
    require (amount >= MIN_BET && amount <= MAX_AMOUNT, "Amount should be within range.");
    require (betMask > 0 && betMask < MAX_BET_MASK, "Mask should be within range.");

    // Check that commit is valid - it has not expired and its signature is valid.
    require (block.number <= commitLastBlock, "Commit has expired.");
    bytes32 signatureHash = keccak256(abi.encodePacked(uint40(commitLastBlock), commit));
    require (secretSigner == ecrecover(signatureHash, 27, r, s), "ECDSA signature is not valid.");

    uint rollUnder;
    uint mask;

    if (modulo <= MAX_MASK_MODULO) {
        // Small modulo games specify bet outcomes via bit mask.
        // rollUnder is a number of 1 bits in this mask (population count).
        // This magic looking formula is an efficient way to compute population
        // count on EVM for numbers below 2**40. For detailed proof consult
        // the dice2.win whitepaper.
        rollUnder = ((betMask * POPCNT_MULT) & POPCNT_MASK) % POPCNT_MODULO;
        mask = betMask;
    } else {
        // Larger modulos specify the right edge of half-open interval of
        // winning bet outcomes.
        require (betMask > 0 && betMask <= modulo, "High modulo range, betMask larger than modulo.");
        rollUnder = betMask;
    }

    // Winning amount and jackpot increase.
    uint possibleWinAmount;
    uint jackpotFee;

    (possibleWinAmount, jackpotFee) = getDiceWinAmount(amount, modulo, rollUnder);

    // Enforce max profit limit.
    require (possibleWinAmount <= amount + maxProfit, "maxProfit limit violation.");

    // Lock funds.
    lockedInBets += uint128(possibleWinAmount);
    jackpotSize += uint128(jackpotFee);

    // Check whether contract has enough funds to process this bet.
    require (jackpotSize + lockedInBets <= address(this).balance, "Cannot afford to lose this bet.");

    // Record commit in logs.
    emit Commit(commit);

    // Store bet parameters on blockchain.
    bet.amount = amount;
    bet.modulo = uint8(modulo);
    bet.rollUnder = uint8(rollUnder);
    bet.placeBlockNumber = uint40(block.number);
    bet.mask = uint40(mask);
    bet.gambler = msg.sender;
}

　　settleBet代码片段:

function settleBet(uint reveal, bytes32 blockHash) external onlyCroupier {
    uint commit = uint(keccak256(abi.encodePacked(reveal)));

    Bet storage bet = bets[commit];
    uint placeBlockNumber = bet.placeBlockNumber;

    // Check that bet has not expired yet (see comment to BET_EXPIRATION_BLOCKS).
    require (block.number > placeBlockNumber, "settleBet in the same block as placeBet, or before.");
    require (block.number <= placeBlockNumber + BET_EXPIRATION_BLOCKS, "Blockhash can't be queried by EVM.");
    require (blockhash(placeBlockNumber) == blockHash);

    // Settle bet using reveal and blockHash as entropy sources.
    settleBetCommon(bet, reveal, blockHash);
}

　　具体的解读还是留给用户自己哈, ^_^.

攻击:
　　当然这种模式也有一定的缺点, 比如服务中止攻击. 即玩家placeBet后, 其行动信息在链上可见, 这时服务可以提前预知结果, 若输了, 可以中止settleBet的调用. 因为玩家不清楚对方到底是那个随机数, 只是看到该下注一直处于pending状态.
　　所以有学者也觉得Dice2Win理论上, 也不是一个真正意义上公平游戏, 具体参见博文: Not a fair game, Dice2win公平性分析. 

总结:
　　其实我想平台为了长久发展, 是不太做这种伤信誉的事的. 总的来说, hash-commit-reveal这种机制, 还是相当不错的, 我看到不少的混合模型的dapp, 采用这种模式来保证游戏的公平性.