剑指offer

1.斐波那契数列

问题描述：

大家都知道斐波那契数列，现在要求输入一个整数 n，请你输出斐波那契数列的第 n 项（从 0 开始，第 0 项为 0）。(n<=39)

方法一：

function Fibonacci(n) {
  if (n == 0 || n == 1) {
    return n;
  }
  var arr = [0, 1];
  for (var i = 2; i <= n; i++) {
    arr.push(arr[arr.length - 1] + arr[arr.length - 2]);
  }
  return arr[n];
}

方法二：

function Fibonacci(n) {
  // write code here
  if (n == 0 || n == 1) {
    return n;
  }
  let triple = [0, 0, 1];
  for (let i = 2; i <= n; i++) {
    triple[0] = triple[1];
    triple[1] = triple[2];
    triple[2] = triple[0] + triple[1];
  }
  return triple[2];
}

方法三：递归（效率低，执行时间长）

function Fibonacci(n) {
  // write code here
  if (n === 0 || n === 1) {
    return n;
  }
  return Fibonacci(n - 1) + Fibonacci(n - 2);
}

2.跳台阶

问题描述：

一只青蛙一次可以跳上 1 级台阶，也可以跳上 2 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

解题思路：

这题其实就是在求斐波那契数列。理解起来也很简单。假设跳到 n 级台阶有 f(n)种方法。根据题目，青蛙在跳上 n 级时有 2 种方法：

• 从 n - 1 级跳 1 级上来
• 从 n - 2 级跳 2 级上来

青蛙跳到 n- 1 级有 f(n-1)种方法，跳到 n- 2 级有 f(n-2)种方法。所以 f(n) = f(n - 1) + f(n - 2)。这就是斐波那契数列的定义式。

function jumpFloor(number) {
  // write code here
  if (number === 1 || number === 2) {
    return number;
  }
  var arr = [1, 2];
  for (let i = 3; i <= number; i++) {
    arr.push(arr[arr.length - 1] + arr[arr.length - 2]);
  }
  return arr[arr.length - 1];
}

3.变态跳台阶

问题描述：

一只青蛙一次可以跳上 1 级台阶，也可以跳上 2 级……它也可以跳上 n 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

解题思路：

假设跳 n 级台阶的跳法数量是 f(n)个。假设跳 n 级台阶的跳法数量是 f(n)个。

那么根据题意，青蛙可能从 n-1 级直接跳上来，也可能从 n-2 级直接跳上来，依次类推：f(n) = f(n - 1) + f(n - 2) + ... + f(1)

同理：f(n - 1) = f(n - 2) + f(n - 3) + ... + f(1)

f(n) = 2 * f(n - 1) = 4 * f(n - 2) = ... = 2 ^ (n - 1)f(1)

其中： f(1) = 1

function jumpFloorII(number) {
  // write code here
  return 2 ** (number - 1);
  // return Math.pow(2,number-1);
}

4.矩形覆盖

问题描述：

我们可以用 21 的小矩形横着或者竖着去覆盖更大的矩形。请问用 n 个 21 的小矩形无重叠地覆盖一个 2*n 的大矩形，总共有多少种方法？

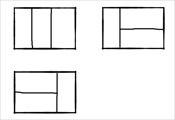
比如 n=3 时，2*3 的矩形块有 3 种覆盖方法：

function rectCover(number) {
  // write code here
  if (number < 1) {
    return 0;
  } else if (number === 1 || number === 2) {
    return number;
  } else {
    var arr = [1, 2];
    for (let i = 3; i <= number; i++) {
      arr.push(arr[arr.length - 1] + arr[arr.length - 2]);
    }
    return arr[arr.length - 1];
  }
}