最近在学习numpy模块中的一维数组时,发现如下矛盾:
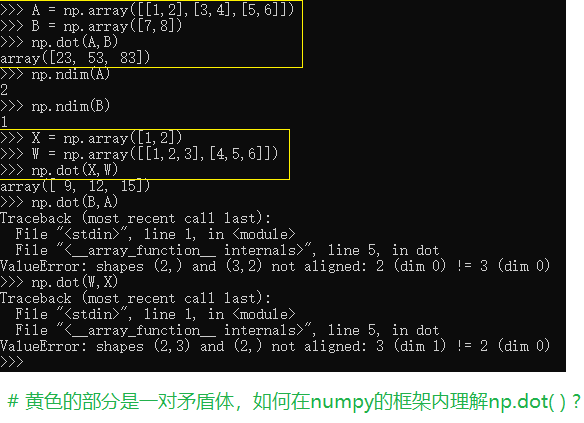
下面是我做的小实验:
import numpy as np # 实验一 A = np.array([[1,2],[3,4],[4,5]]) # 这个是3*2的矩阵 print(A) print(A.shape) B = np.array([1,2]) # 这个矩阵式什么形状呢,根据矩阵乘法规则,B应该式2*1的矩阵 print(B) print(B.shape) C = np.dot(A,B) # B的形状由它的乘积决定 print(C) # 实验二 X = np.array([1,2]) # 所以,X是1*2的矩阵 print(X) print(X.shape) W = np.array([[1,2,3],[4,5,6]]) # W矩阵的形状式唯一确定的2*3 print(W) print(W.shape) M = np.dot(X,W) # 因为X矩阵的形状由该代码所决定 print(M) # 通过上面的实验很容易看出,np.array([1,2])一会是行向量,一会是列向量 # 下面我要验证的是当一维向量在左边的时候是行向量,在右边的时候是列向量 row = np.array([1,2,3]) column = np.array([1,2,3]) muply = np.dot(row,column) print(muply) # 下面我要验证的是到底右边是不是永远都是列向量 row1 = np.array([1,2,3]) column1 = np.array([1,2,3]) column2 = column1.reshape(-1,1) print(column2.shape) print(column2) H = np.dot(column2,row1) print(H)
结论:当一维数组在乘号的左边时是行向量,反之,是列向量。