DLX算法

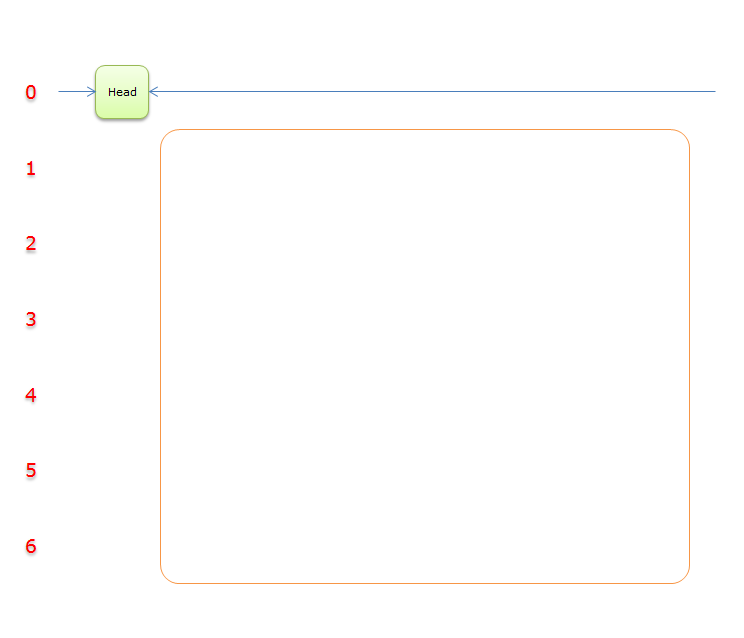
理解DLX算法之前首先了解精确覆盖问题和重复覆盖问题

精确覆盖问题

何为精确覆盖问题

　　在一个全集X中若干子集的集合为S，精确覆盖（Exactcover）是指，S的子集S*，满足X中的每一个元素在S*中恰好出现一次。

定义　

　　满足以下条件的集合为一个精确覆盖： 
　　　　S*中任意两个集合没有交集，即X中的元素在S*中出现最多一次 
　　　　S*中集合的全集为X，即X中的元素在S*中出现最少一次 
　　　　合二为一，即X中的元素在S*中出现恰好一次。

　　举例

　　令={N,O,E,P}是集合X={1,2,3,4}的一个子集，并满足： 
　　　　N={} 
　　　　O={1,3} 
　　　　E={2,4} 
　　　　P={2,3}. 
　　　　其中一个子集{O,E}是X的一个精确覆盖,因为O={1,3}而E={2,4}的并集恰好是X={1,2,3,4}。同理，{N,O,E}也是X.的一个精确覆盖。空集并不影响结论。

精确覆盖问题的表示方式

　　一般的，我们用一个集合s包含s中的元素的单向关系表示精确覆盖问题。常用的有以下两种方法：

• 矩阵表示法

　　包含关系可以用一个关系矩阵表示。.矩阵每行表示S的一个子集，每列表示X中的一个元素。矩阵行列交点元素为1表示对应的元素在对应的集合中，不在则为0。 

　　通过这种矩阵表示法，求一个精确覆盖转化为求矩阵的若干个行的集合，使每列有且仅有一个1。同时，该问题也是精确覆盖的典型例题之一。

　　下表为其中一个例子：

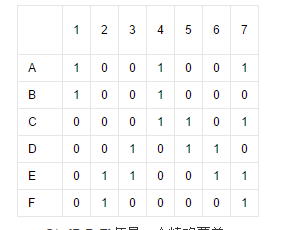
S*={B,D,F}便是一个精确覆盖。

• 图论表示法

　　可将精确覆盖问题转化为一个二分图，左侧为集合，右侧为元素，左侧集合若与右侧元素有包含关系则连边，通过将左侧节点与其所有边保留与否求解一个右侧的每一个节点恰好有一条边的匹配。

重复覆盖问题

 　即选取一个01矩阵中的几行，使这几行组成的新矩阵的每一列至少有一个1，也就是说每一列上可以有多个1。 该问题在精确覆盖问题上减少了一个约束条件。

Dancing Links X 算法

历史

　　算法大师Donald E.Knuth（《计算机程序设计艺术》的作者）提出了DLX（Dancing Links X）算法。实际上，他把上面求解的过程称为X算法，而他提出的舞蹈链（Dancing Links）实际上并不是一种算法，而是一种数据结构。一种非常巧妙的数据结构，他的数据结构在缓存和回溯的过程中效率惊人，不需要额外的空间，以及近乎线性的时间。而在整个求解过程中，指针在数据之间跳跃着，就像精巧设计的舞蹈一样，故Donald E.Knuth把它称为Dancing Links（中文译名舞蹈链）。

算法思想

　　

Dancing Links的核心是基于双向链的方便操作（移除、恢复加入）

我们用例子来说明

假设双向链的三个连续的元素，A1、A2、A3，每个元素有两个分量Left和Right，分别指向左边和右边的元素。由定义可知

A1.Right=A2，A2.Right=A3

A2.Left=A1，A3.Left=A2

在这个双向链中，可以由任一个元素得到其他两个元素，A1.Right.Right=A3，A3.Left.Left=A1等等

现在把A2这个元素从双向链中移除（不是删除）出去，那么执行下面的操作就可以了

A1.Right=A3，A3.Left=A1

那么就直接连接起A1和A3。A2从双向链中移除出去了。但仅仅是从双向链中移除了，A2这个实体还在，并没有删除。只是在双向链中遍历的话，遍历不到A2了。

那么A2这个实体中的两个分量Left和Right指向谁？由于实体还在，而且没有修改A2分量的操作，那么A2的两个分量指向没有发生变化，也就是在移除前的指向。即A2.Left=A1和A2.Right=A3

如果此时发现，需要把A2这个元素重新加入到双向链中的原来的位置，也就是A1和A3的中间。由于A2的两个分量没有发生变化，仍然指向A1和A3。那么只要修改A1的Right分量和A3的Left就行了。也就是下面的操作

A1.Right=A2，A3.Left=A2

仔细想想，上面两个操作（移除和恢复加入）对应了什么？是不是对应了之前的算法过程中的关键的两步？

移除操作对应着缓存数据、恢复加入操作对应着回溯数据。而美妙的是，这两个操作不再占用新的空间，时间上也是极快速的

在很多实际运用中，把双向链的首尾相连，构成循环双向链

Dancing Links用的数据结构是交叉十字循环双向链

而Dancing Links中的每个元素不仅是横向循环双向链中的一份子，又是纵向循环双向链的一份子。

因为精确覆盖问题的矩阵往往是稀疏矩阵（矩阵中，0的个数多于1），Dancing Links仅仅记录矩阵中值是1的元素。

Dancing Links中的每个元素有6个分量

分别：Left指向左边的元素、Right指向右边的元素、Up指向上边的元素、Down指向下边的元素、Col指向列标元素、Row指示当前元素所在的行

Dancing Links还要准备一些辅助元素（为什么需要这些辅助元素？没有太多的道理，大师认为这能解决问题，实际上是解决了问题）

Ans（）：Ans数组，在求解的过程中保留当前的答案，以供最后输出答案用。

Head元素：求解的辅助元素，在求解的过程中，当判断出Head.Right=Head（也可以是Head.Left=Head）时，求解结束，输出答案。Head元素只有两个分量有用。其余的分量对求解没啥用

C元素：辅助元素，称列标元素，每列有一个列标元素。本文开始的题目的列标元素分别是C1、C2、C3、C4、C5、C6、C7。每一列的元素的Col分量都指向所在列的列标元素。列标元素的Col分量指向自己（也可以是没有）。在初始化的状态下，Head.Right=C1、C1.Right=C2、……、C7.Right=Head、Head.Left=C7等等。列标元素的分量Row=0，表示是处在第0行。

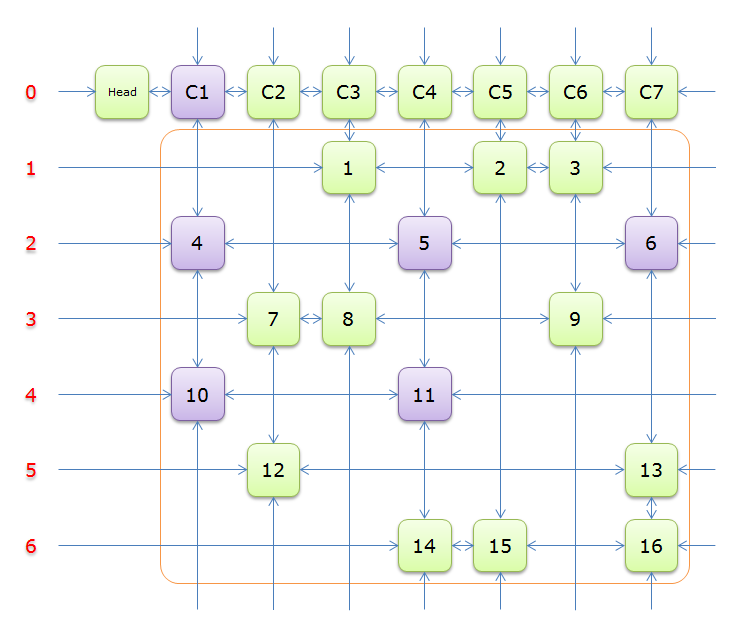
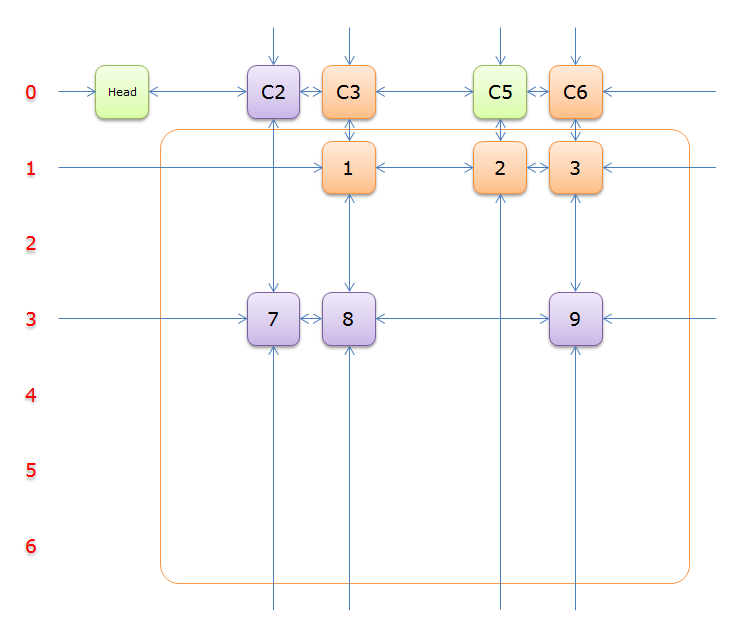
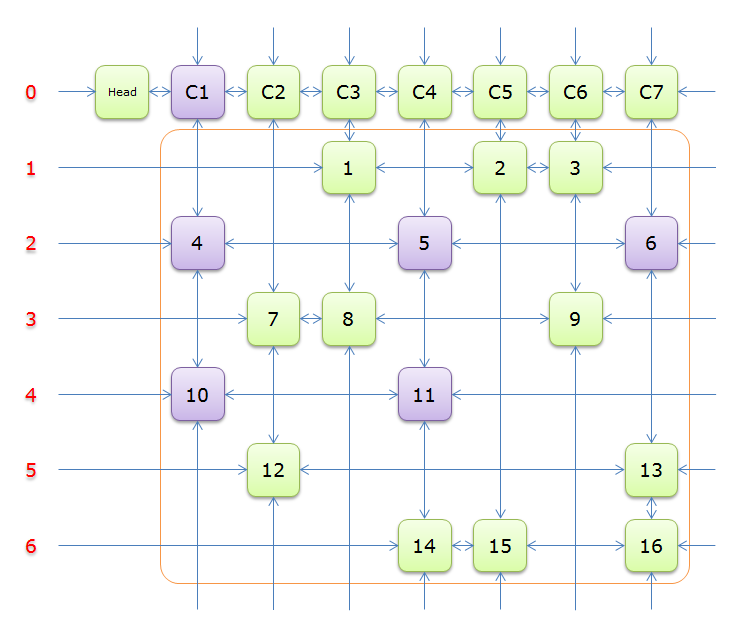
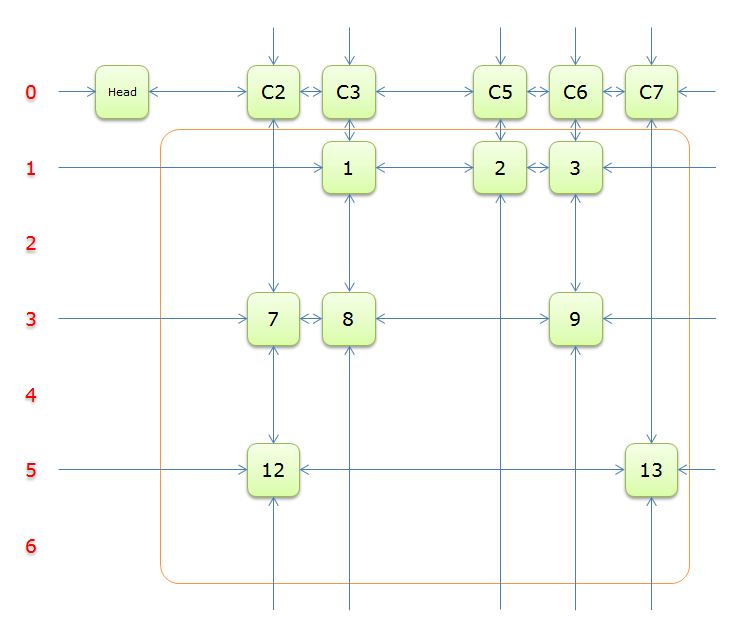
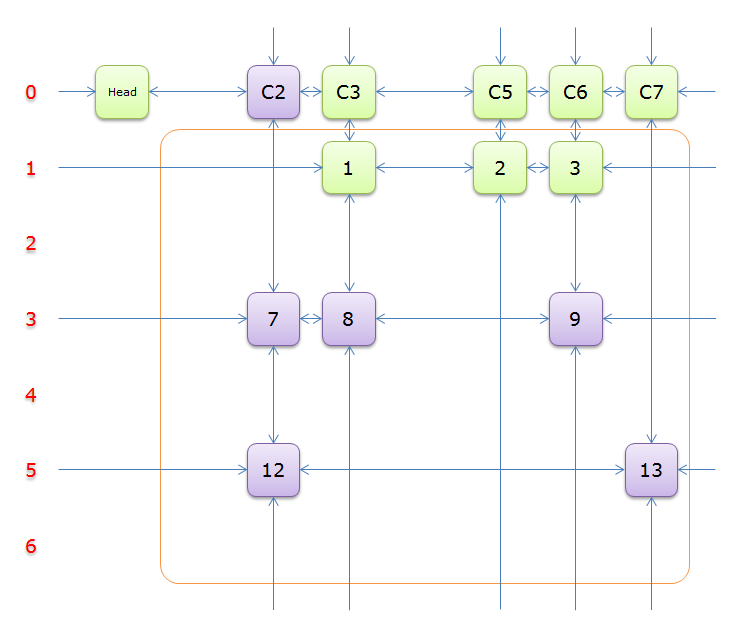
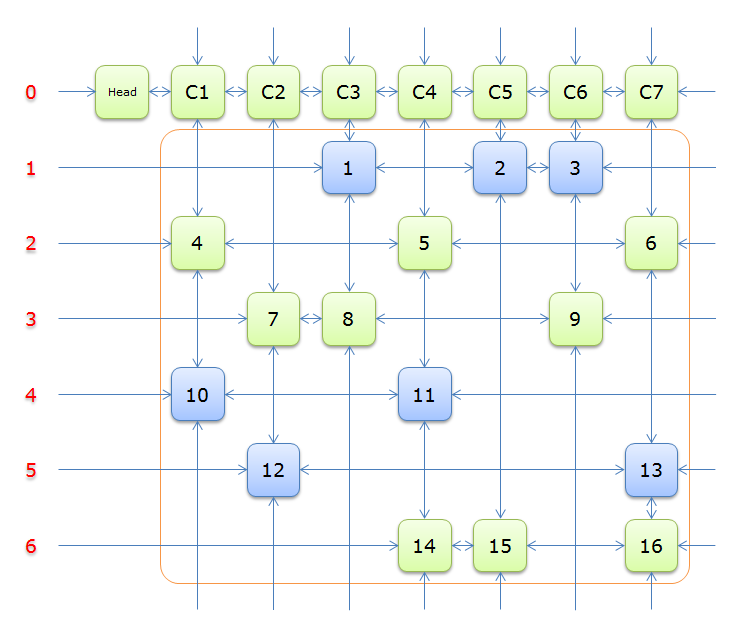
下图就是根据题目构建好的交叉十字循环双向链（构建的过程后面的详述）

　

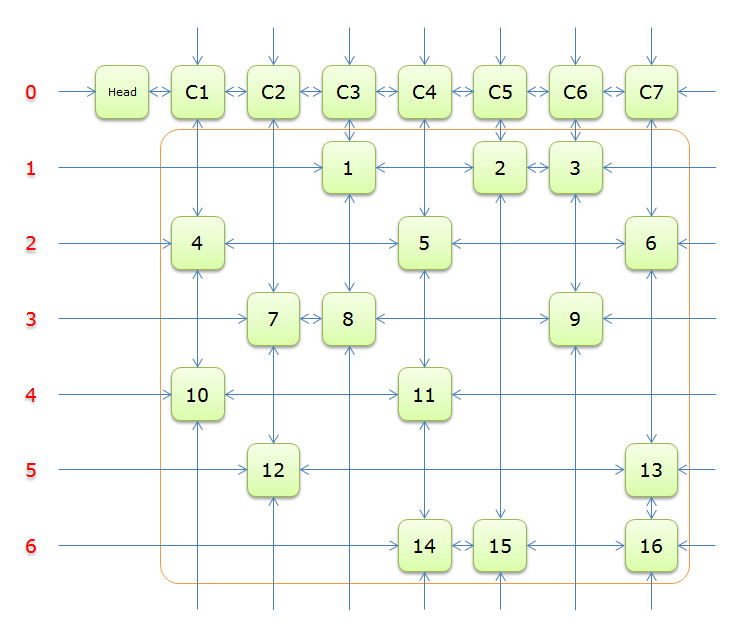
就上图解释一下

每个绿色方块是一个元素，其中Head和C1、C2、……、C7是辅助元素。橙色框中的元素是原矩阵中1的元素，给他们标上号（从1到16）

左侧的红色，标示的是行号，辅助元素所在的行是0行，其余元素所在的行从1到6

每两个元素之间有一个双向箭头连线，表示双向链中相邻两个元素的关系（水平的是左右关系、垂直的是上下关系）

单向的箭头并不是表示单向关系，而因为是循环双向链，左侧的单向箭头和右侧的单向箭头（上边的和下边的）组成了一个双向箭头，例如元素14左侧的单向箭头和元素16右侧的单项箭头组成一个双向箭头，表示14.Left=16、16.Right=14；同理，元素14下边的单项箭头和元素C4上边的单向箭头组成一个双向箭头，表示14.Down=C4、C4.Up=14

接下来，利用图来解释Dancing Links是如何求解精确覆盖问题

1、首先判断Head.Right=Head？若是，求解结束，输出解；若不是，求解还没结束，到步骤2（也可以判断Head.Left=Head？）

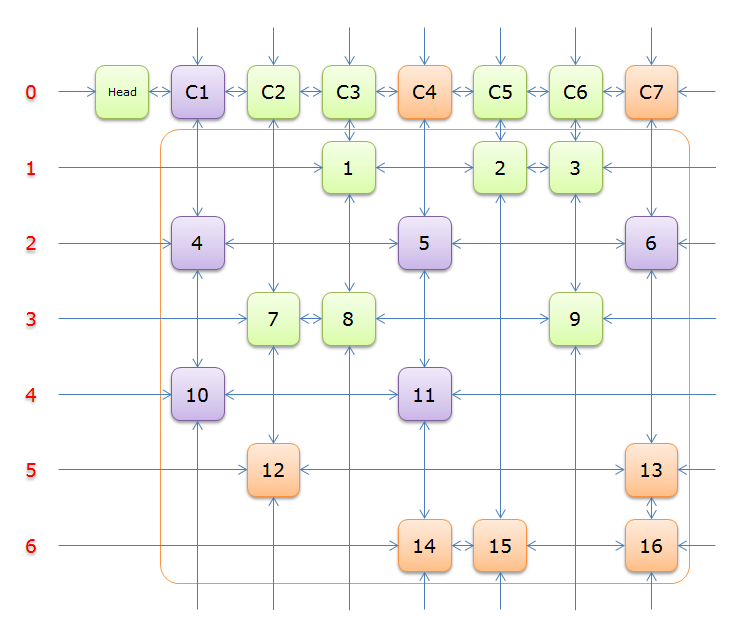
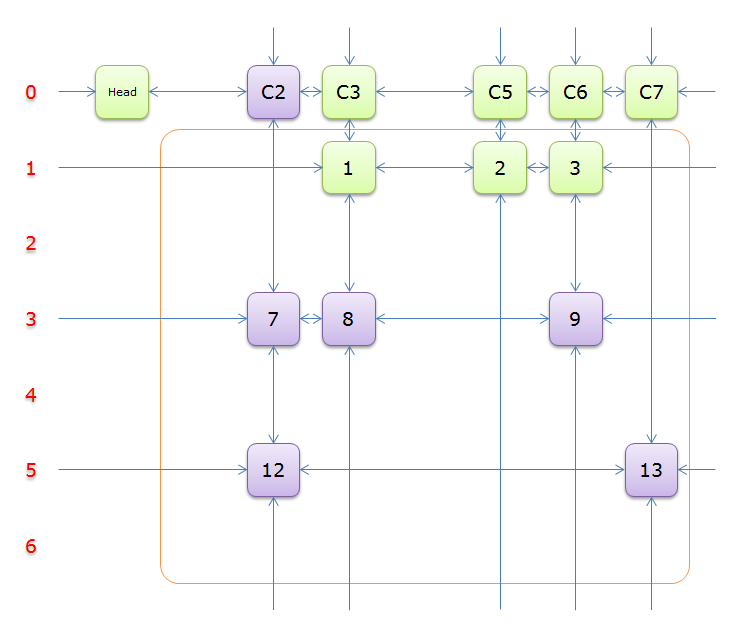
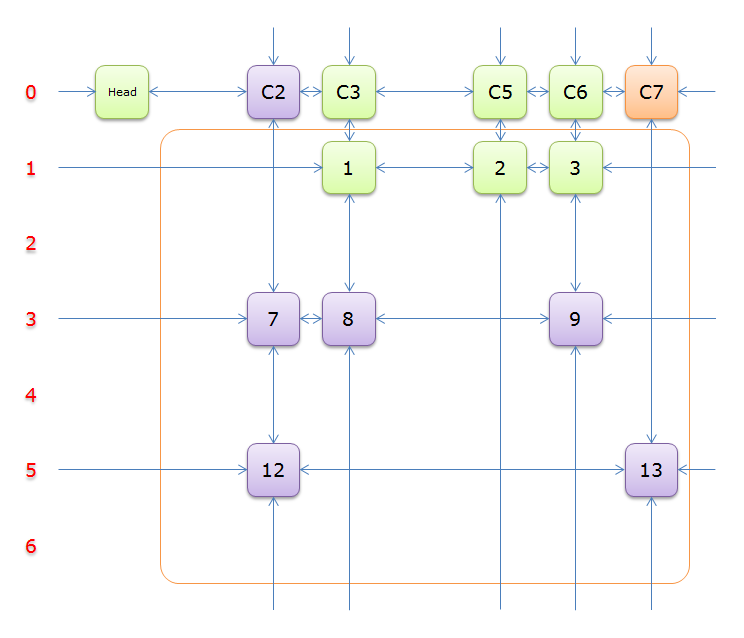
2、获取Head.Right元素，即元素C1，并标示元素C1（标示元素C1，指的是标示C1、和C1所在列的所有元素、以及该元素所在行的元素，并从双向链中移除这些元素）。如下图中的紫色部分。

如上图可知，行2和行4中的一个必是答案的一部分（其他行中没有元素能覆盖列C1），先假设选择的是行2

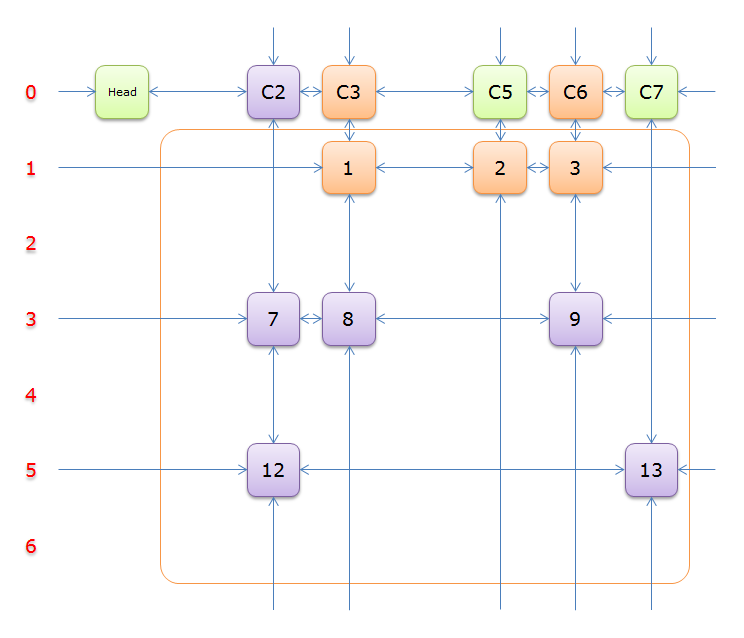
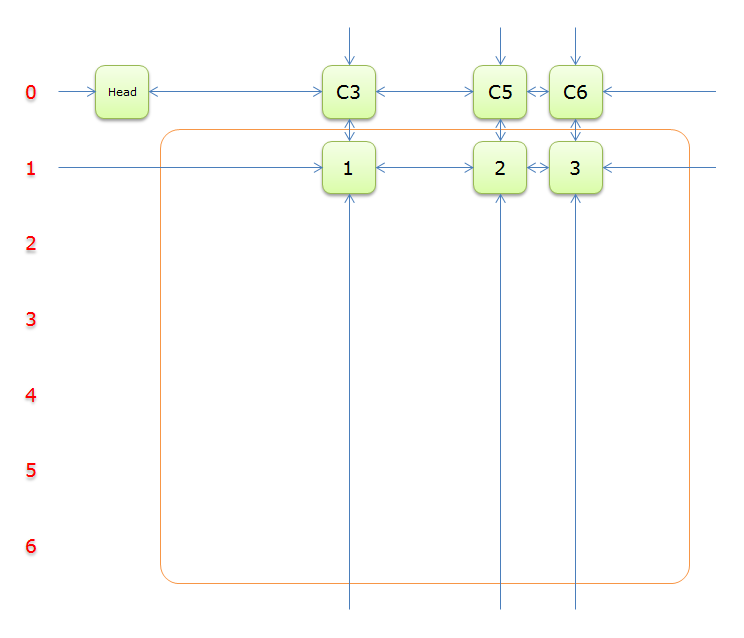
3、选择行2（在答案栈中压入2），标示该行中的其他元素（元素5和元素6）所在的列首元素，即标示元素C4和标示元素C7，下图中的橙色部分。

注意的是，即使元素5在步骤2中就从双向链中移除，但是元素5的Col分量还是指向元素C4的，这里体现了双向链的强大作用。

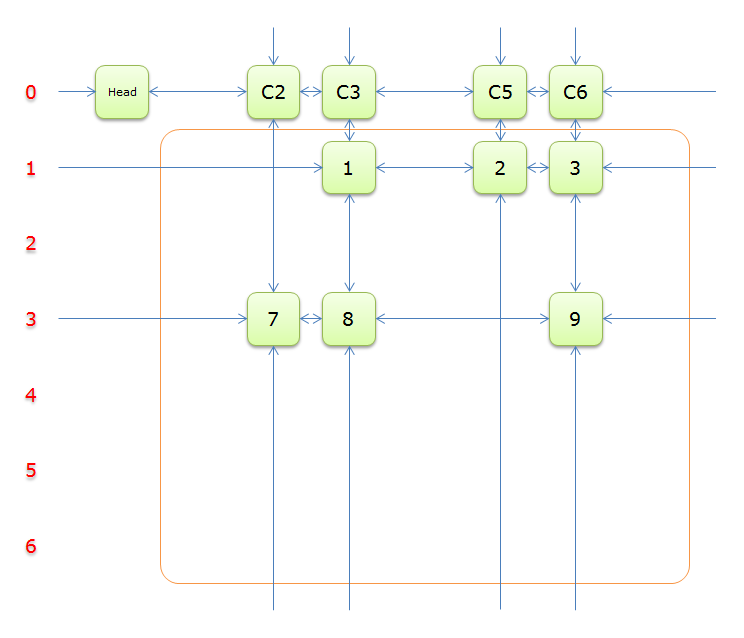
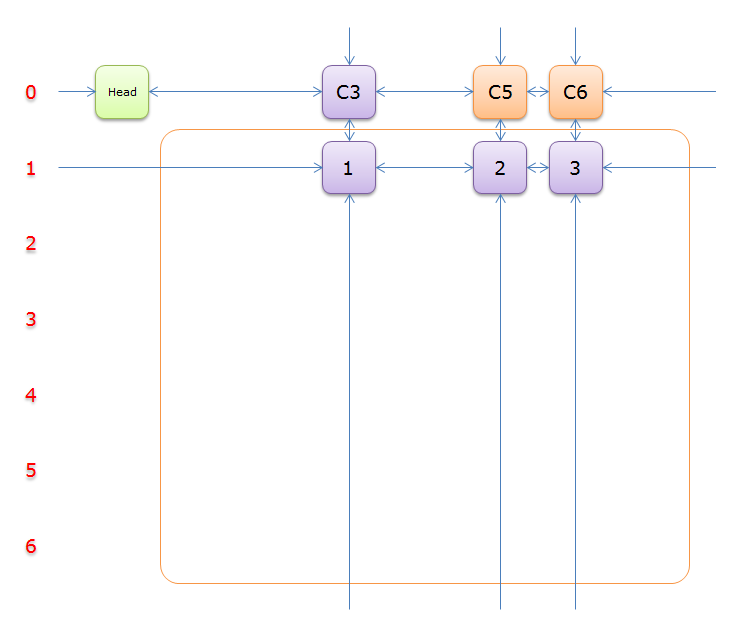
把上图中的紫色部分和橙色部分移除的话，剩下的绿色部分就如下图所示

一下子空了好多，是不是转换为一个少了很多元素的精确覆盖问题？，利用递归的思想，很快就能写出求解的过程来。我们继续完成求解过程

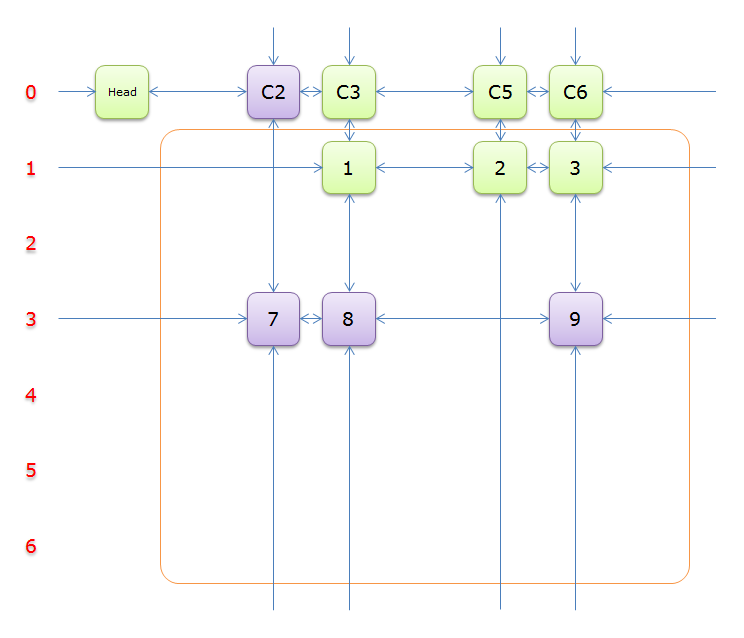
4、获取Head.Right元素，即元素C2，并标示元素C2。如下图中的紫色部分。

如图，列C2只有元素7覆盖，故答案只能选择行3

5、选择行3（在答案栈中压入3），标示该行中的其他元素（元素8和元素9）所在的列首元素，即标示元素C3和标示元素C6，下图中的橙色部分。

把上图中的紫色部分和橙色部分移除的话，剩下的绿色部分就如下图所示

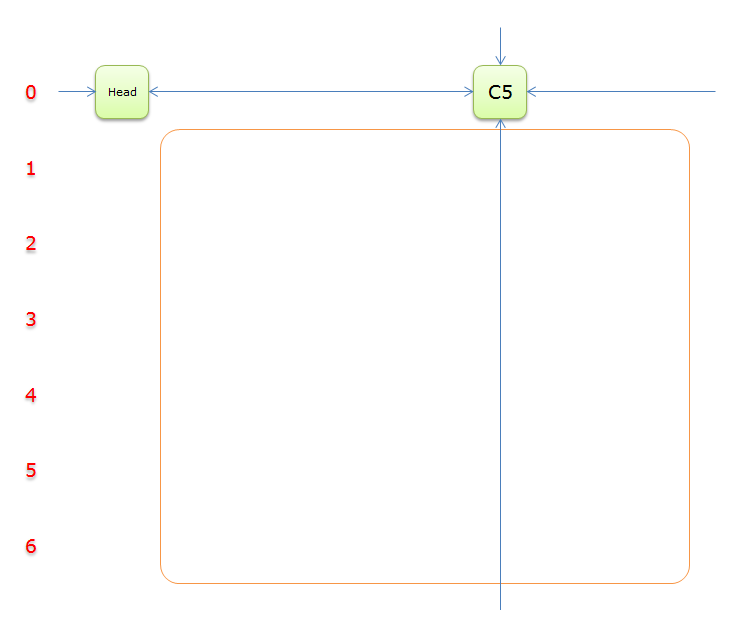
6、获取Head.Right元素，即元素C5，元素C5中的垂直双向链中没有其他元素，也就是没有元素覆盖列C5。说明当前求解失败。要回溯到之前的分叉选择步骤（步骤2）。那要回标列首元素（把列首元素、所在列的元素，以及对应行其余的元素。并恢复这些元素到双向链中），回标列首元素的顺序是标示元素的顺序的反过来。从前文可知，顺序是回标列首C6、回标列首C3、回标列首C2、回标列首C7、回标列首C4。表面上看起来比较复杂，实际上利用递归，是一件很简单的事。并把答案栈恢复到步骤2（清空的状态）的时候。又回到下图所示

7、由于之前选择行2导致无解，因此这次选择行4（再无解就整个问题就无解了）。选择行4（在答案栈中压入4），标示该行中的其他元素（元素11）所在的列首元素，即标示元素C4，下图中的橙色部分。

把上图中的紫色部分和橙色部分移除的话，剩下的绿色部分就如下图所示

8、获取Head.Right元素，即元素C2，并标示元素C2。如下图中的紫色部分。

如图，行3和行5都可以选择

9、选择行3（在答案栈中压入3），标示该行中的其他元素（元素8和元素9）所在的列首元素，即标示元素C3和标示元素C6，下图中的橙色部分。

把上图中的紫色部分和橙色部分移除的话，剩下的绿色部分就如下图所示

10、获取Head.Right元素，即元素C5，元素C5中的垂直双向链中没有其他元素，也就是没有元素覆盖列C5。说明当前求解失败。要回溯到之前的分叉选择步骤（步骤8）。从前文可知，回标列首C6、回标列首C3。并把答案栈恢复到步骤8（答案栈中只有4）的时候。又回到下图所示

11、由于之前选择行3导致无解，因此这次选择行5（在答案栈中压入5），标示该行中的其他元素（元素13）所在的列首元素，即标示元素C7，下图中的橙色部分。

把上图中的紫色部分和橙色部分移除的话，剩下的绿色部分就如下图所示

12、获取Head.Right元素，即元素C3，并标示元素C3。如下图中的紫色部分。

13、如上图，列C3只有元素1覆盖，故答案只能选择行3（在答案栈压入1）。标示该行中的其他元素（元素2和元素3）所在的列首元素，即标示元素C5和标示元素C6，下图中的橙色部分。

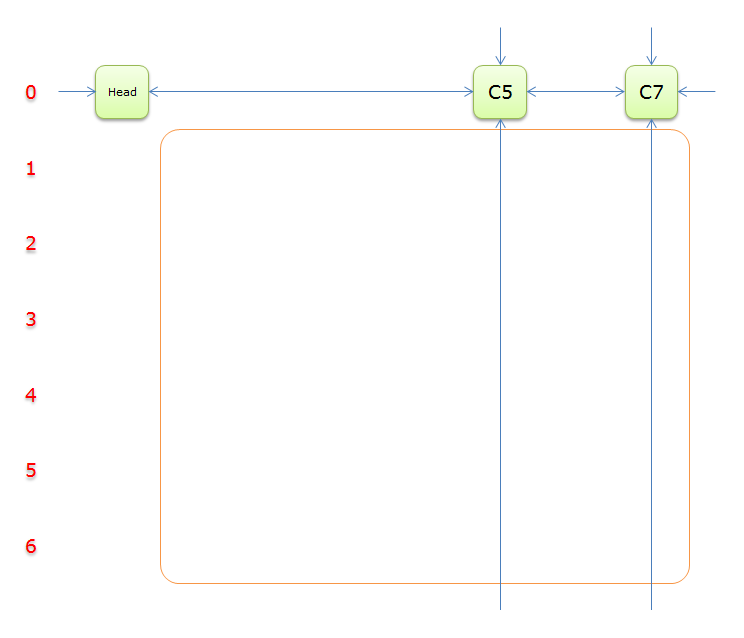
把上图中的紫色部分和橙色部分移除的话，剩下的绿色部分就如下图所示

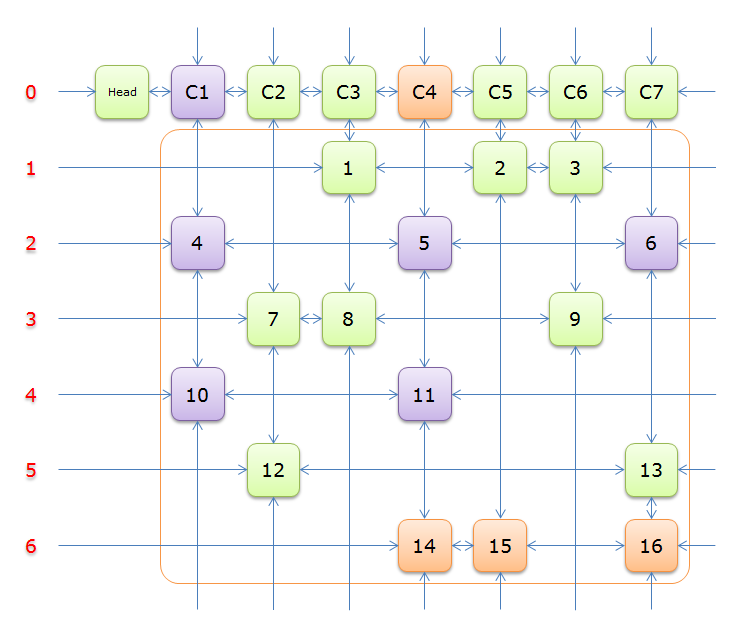
14、因为Head.Right=Head。故，整个过程求解结束。输出答案，答案栈中的答案分别是4、5、1。表示该问题的解是第4、5、1行覆盖所有的列。如下图所示（蓝色的部分）

从以上的14步来看，可以把Dancing Links的求解过程表述如下

1、Dancing函数的入口

2、判断Head.Right=Head？，若是，输出答案，返回True，退出函数。

3、获得Head.Right的元素C

4、标示元素C

5、获得元素C所在列的一个元素

6、标示该元素同行的其余元素所在的列首元素

7、获得一个简化的问题，递归调用Daning函数，若返回的True，则返回True，退出函数。

8、若返回的是False，则回标该元素同行的其余元素所在的列首元素，回标的顺序和之前标示的顺序相反

9、获得元素C所在列的下一个元素，若有，跳转到步骤6

10、若没有，回标元素C，返回False，退出函数。

之前的文章的表述，为了表述简单，采用面向对象的思路，说每个元素有6个分量，分别是Left、Right、Up、Down、Col、Row分量。

但在实际的编码中，用数组也能实现相同的作用。例如：用Left（）表示所有元素的Left分量，Left（1）表示元素1的Left分量

在前文中，元素分为Head元素、列首元素（C1、C2等）、普通元素。在编码中，三种元素统一成一种元素。如上题，0表示Head元素，1表示元素C1、2表示元素C2、……、7表示元素C7，从8开始表示普通元素。这是统一后，编码的简便性。利用数组的下标来表示元素，宛若指针一般。

精确覆盖例题：Sudoku ZOJ - 3122   链接：https://zoj.pintia.cn/problem-sets/91827364500/problems/91827367537

代码：

#include <cstdio>
#include <fstream>
#include <algorithm>
#include <cmath>
#include <deque>
#include <vector>
#include <queue>
#include <string>
#include <cstring>
#include <map>
#include <stack>
#include <set>
#include <sstream>
#include <iostream>
#define mod 1000000007
#define eps 1e-6
#define ll long long
#define INF 0x3f3f3f3f
using namespace std;

const int maxn=18000;
//ans用来记录答案的编号
int ans[maxn];
struct DLX
{

    //左右上下，四个数组
    int left[maxn],right[maxn],up[maxn],down[maxn];
    //列数组，头数组,loc代表这个数在数独中的位置和数值
    int col[maxn],head[maxn],loc[maxn][3];
    //num数组保存每列有几个数，id为编号
    int num[1030],id;
    //创建有m列的矩阵
    void init(int n)
    {
        for(int i=0;i<=n;i++)
        {
            up[i]=down[i]=i;
            left[i]=i-1;
            right[i]=i+1;
        }
        left[0]=n; right[n]=0;
        id=n;
        memset(num,0,sizeof(num));
        memset(head,-1,sizeof(head));
    }
    //插入位于x,y的数，并对其上下左右，列和编号初始化，对px,py,pz存入loc数组
    void Link(int x,int y,int px,int py,int k)
    {
        ++id;
        down[id]=y; 
        up[id]=up[y];
        down[up[y]]=id;
        up[y]=id;
        loc[id][0]=px,loc[id][1]=py,loc[id][2]=k;//存放数的位置和数
        col[id]=y;
        num[y]++;//此列1的数量加一
        if(head[x]==-1)
        {
                head[x]=left[id]=right[id]=id;
        }
        else
        {
            int a=head[x];
            int b=right[a];
            left[id]=a; right[a]=id;
            right[id]=b; left[b]=id;
            head[x]=id;
        }
    }
    //移除c列和c列上数所在的每一行，
    void Remove(int c)
    {
        left[right[c]]=left[c];
        right[left[c]]=right[c];
        for(int i=down[c];i!=c;i=down[i])
            for(int j=right[i];j!=i;j=right[j])
        {
            up[down[j]]=up[j];
            down[up[j]]=down[j];
            num[col[j]]--;
        }
    }
    //恢复c列和c列上数所在的每一行，
    void Resume(int c)
    {
        for(int i=up[c];i!=c;i=up[i])
            for(int j=right[i];j!=i;j=right[j])
        {
            num[col[j]]++;
            up[down[j]]=j;
            down[up[j]]=j;
        }
        left[right[c]]=c;
        right[left[c]]=c;
    }
    bool dfs(int step)
    {
        //如果走到第256步时已走完所有的数独中的数，所以退出
        if(step==256) return true;
        //如果头指向第0列，说明所有列已删除
        if(right[0]==0) return false;
        int c=right[0];
        //用循环是c优先指向列中数少的列
        for(int i=right[0];i;i=right[i])
        {
             if(num[i]<num[c])
             { 
                 c=i;
             }
        }
        //删除第c列
        Remove(c);
        for(int i=down[c];i!=c;i=down[i])
        {
            //记录每此循环选的编号
            ans[step]=i;
            //遍历i所在的行，并删除j所在的列
            for(int j=right[i];j!=i;j=right[j]) Remove(col[j]);
            //如果循环下去有解，则返回true
            if(dfs(step+1)) return true;
            //遍历i所在的行，并恢复j所在的列
            for(int j=left[i];j!=i;j=left[j]) Resume(col[j]);
        }
        //恢复第c列
        Resume(c);
        //所有操作完成后仍无解，则返回false
        return false;
    }
}dlx;
int main()
{
    //str数组存放输入的数据
    char str[260];
    int kase=0;
    while(cin>>str)
    {
        //换行
        if(kase)
        {
            cout<<endl;
        }
        kase++;
        for(int i=1;i<=15;i++)
        {
            cin>>str+i*16;
        }
        dlx.init(256*4);
        int r=0,js=0;//r代表行
        for(int x=0;x<16;x++)
        {    for(int y=0;y<16;y++)
            {
                char ch=str[js];
                js++;
                int s=(x/4)*4+y/4;//宫
                int a,b,c,d;//a表示约束一，b表示约束二，c表示约束三,d表示约束四
                if(ch=='-')
                {
                    //此位置上可能是1到16，
                    for(int i=1;i<=16;i++)
                    {
                        a=x*16+y+1;
                        b=x*16+i+256;
                        c=y*16+i+256+256;
                        d=s*16+i+256+256+256;
                        ++r;
                        dlx.Link(r,a,x,y,i);
                        dlx.Link(r,b,x,y,i);
                        dlx.Link(r,c,x,y,i);
                        dlx.Link(r,d,x,y,i);
                    }
                }
                else
                {
                    int i=ch-64;
                    a=x*16+y+1;
                    b=x*16+i+256;
                    c=y*16+i+256+256;
                    d=s*16+i+256+256+256;
                    ++r;
                    dlx.Link(r,a,x,y,i);
                    dlx.Link(r,b,x,y,i);
                    dlx.Link(r,c,x,y,i);
                    dlx.Link(r,d,x,y,i);
                }
            }
        }
        dlx.dfs(0);
        char res[16][16];
        for(int i=0;i<256;i++)//将答案存放到一个数独数组中
        {
            int a=ans[i];
            int x=dlx.loc[a][0],y=dlx.loc[a][1],k=dlx.loc[a][2]-1;
            res[x][y]=k+'A';
        }
        for(int i=0;i<16;i++)
        {
            for(int j=0;j<16;j++)
            {
                printf("%c",res[i][j]);
            }
            printf("
");
        }
    }
   
}

重复覆盖例题：Airport HDU - 5046  链接：https://vjudge.net/problem/HDU-5046

代码：

#include <cstdio>
#include <fstream>
#include <algorithm>
#include <cmath>
#include <deque>
#include <vector>
#include <queue>
#include <string>
#include <cstring>
#include <map>
#include <stack>
#include <set>
#include <sstream>
#include <iostream>
#define mod 998244353
#define eps 1e-6
#define ll long long
#define INF 0x3f3f3f3f
using namespace std;

const int maxn=4010;
int k;
struct 
{
    //左右上下，四个数组
    int left[maxn],right[maxn],up[maxn],down[maxn];
    //头数组，列数组
    int head[65],col[maxn];
    //num数组保存每列有几个数，id为编号
    int num[65],id;
    //创建有m列的矩阵
    void init(int m)
    {
        for(int i=0;i<=m;i++)
        {
            left[i]=i-1;
            right[i]=i+1;
            up[i]=down[i]=i;
            col[i]=i;
        }
        id=m;
        left[0]=m;
        right[m]=0;
        memset(head,-1,sizeof(head));
        memset(num,0,sizeof(num));
    }
    //插入位于x,y的数，并对其上下左右，列和编号初始化
    void link(int x,int y)
    {
        id++;
        down[id]=down[y];
        up[down[y]]=id;
        up[id]=y;
        down[y]=id;
        num[y]++;
        col[id]=y;
        if(head[x]==-1)
        {
            head[x]=left[id]=right[id]=id;
        }
        else
        {
            right[id]=right[head[x]];
            left[right[head[x]]]=id;
            left[id]=head[x];
            right[head[x]]=id;
        }
    }
    //只移除c所在的一列和c所在列上数所在的每一行
    void remove(int c)
    {
        for(int i=down[c];i!=c;i=down[i])
        {
            left[right[i]]=left[i];
            right[left[i]]=right[i];
        }
    }
    //恢复c所在的一列和c所在列上数所在的每一行
    void reback(int c)
    {
        for(int i=up[c];i!=c;i=up[i])
        {
            left[right[i]]=right[left[i]]=i;
        }
    }
    bool bj[maxn];
    //计算还需要多少步
    int A()
    {
        int ans=0;
        for(int c=right[0];c!=0;c=right[c])
        {
            bj[c]=true;
        }
        for(int c=right[0];c!=0;c=right[c])
        {
            if(bj[c])
            {
                ans++;
                bj[c]=false;
                for(int i=down[c];i!=c;i=down[i])
                {
                    for(int j=right[i];j!=i;j=right[j])
                    {
                        bj[col[j]]=false;
                    }
                }
            }
        }
        return ans;
    }
    //核心函数，step表示步数
    bool danc(int step)
    {
        //如果还要走的步数加上已走的步数，比现有的答案多，则不需要走了，因此退出
        if(A()+step>k)//剪枝
        {
            return false;
        }
        //如果头指向第0列，说明所有列已删除
        if(right[0]==0)
        {
            return step<=k;
        }
        int c=right[0];
        //用循环是c优先指向列中数少的列
        for(int i=c;i!=0;i=right[i])
        {
            if(num[i]<num[c])
            {
                c=i;
            }
        }
        //遍历c列中的数
        for(int i=down[c];i!=c;i=down[i])
        {
            //删除i列
            remove(i);
            //遍历i所在的行，并删除j所在的列
            for(int j=right[i];j!=i;j=right[j])
            {
                remove(j);
            }
            //如果循环下去有解，则返回true
            if(danc(step+1))
            {
                return true;
            }
            //遍历i所在的行，并恢复j所在的列
            for(int j=left[i];j!=i;j=left[j])
            {
                reback(j);
            }
            //恢复i列
            reback(i);
        }
        //所有操作完成后仍无解，则返回false
        return false;
    }
}dlx;
struct node//小岛信息
{
    ll x,y;
}no[65];
ll dis(node a,node b)//计算距离
{
    ll dx=a.x-b.x;
    if(dx<0)
    {
        dx=-dx;
    }
    ll dy=a.y-b.y;
    if(dy<0)
    {
        dy=-dy;
    }
    return dx+dy;
}
int main()
{
    int t,ans=0;;
    scanf("%d",&t);
    while(t--)
    {
        ans++;
        int n;
        ll x[65],y[65];
        scanf("%d %d",&n,&k);
        for(int i=1;i<=n;i++)
        {
            scanf("%lld %lld",&no[i].x,&no[i].y);
        }
        ll le=0,rig=100000000000LL;
        //二分法一步一步缩小距离
        while(rig-le>0)
        {
            dlx.init(n);
            ll mid=(rig+le)/2;
            for(int i=1;i<=n;i++)
            {
                for(int j=1;j<=n;j++)
                {
                    if(dis(no[i],no[j])<=mid)//岛之间的距离比航距小时
                    {
                        dlx.link(i,j);
                    }
                }
            }
            if(dlx.danc(0))//如果当前航距需要的最少飞机的数量比k小为true
            {
                rig=mid;
            }
            else
            {
                le=mid+1;
            }
        }
        printf("Case #%d: %lld
",ans,le);
    }
}