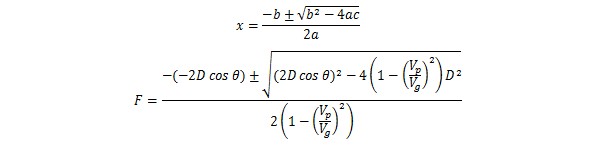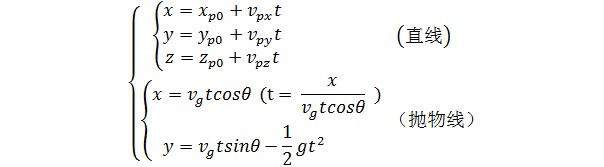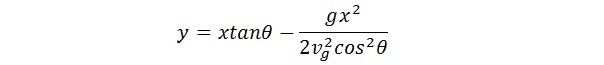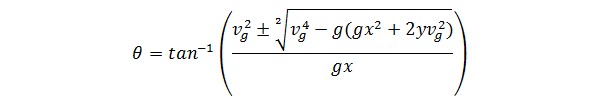http://download.jikexueyuan.com/detail/id/432.html
弹道计算是游戏里常见的问题,其中关于击中移动目标的自动计算提前量的话题,看似简单,其实还是挺复杂的数学。网上这方面的资料还真不多,而且都是写的含含糊糊。抽空总结一下自己的方法。
讨论的前提是,假设目标是在3D空间里以匀速直线方式运动。
1.直线弹道
在不考虑重力和空气阻力影响的情况下,子弹的弹道呈直线运动。这种情况下,其实是个纯平面几何空间的问题,不需要微积分和线代知识。
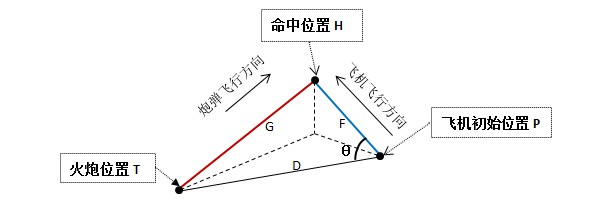
分析的情况如下图:
虽然在3D空间飞行,但火炮命中时,命中点和火炮位置、飞机初始位置处于一个三角形上,只需要平面几何知识就能解决问题。在这个三角形中,飞机起始位置P和火炮T的位置是确定的,飞机的飞行方向也是确定的,所以θ角是已知的,D的长度也是已知的,F和G的长度虽然不知道,但在命中点H相遇的时候经过的时间t都是一样的,所以F/G的比例实际等于两者速度的比例,而两者的速度都是已知的。这样就可以用高中的余弦公式来解决这个求边长的问题:
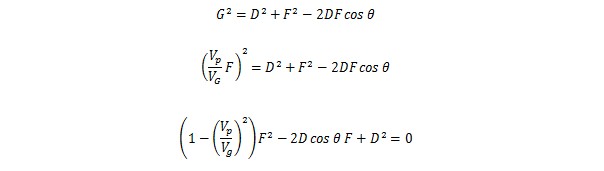
其中V_p和V_g分别代表飞机的速度和炮弹飞行的速度,这是一个标准的1元2次方程,化简、消元对某这么一个非数学专业的来说太麻烦了,直接用求根公式求解吧,有好的化简方法请指教。
在Unity中实现的方法:
Vector3 hitPoint = Vector3.zero;//存放命中点坐标
//假设飞机物体是aircraft,炮塔物体是gun 两者间的方向向量就是两种世界坐标相减
Vector3 D = gun.transform.position - aircraft.transform.position;
//用飞机transform的TransformDirection方法把前进方向变换到世界坐标,就是飞机飞行的世界方向向量了
Vector3 aircraftDirection = aircraft.transform.TransformDirection(Vector3.foward);
//再用Vector3.Angle方法求出与飞机前进方向之间的夹角
float THETA = Vector3.Angle(D,aircraftDirection);
float DD = D.magnitude;//D是飞机炮塔间方向向量,D的magnitued就是两种间距离
float A =1-Mathf.Pow((gunVelocity/aircraftVelocity),2);//假设炮弹的速度是gunVeloctiy飞机的飞行线速度是aircraftVeloctiy
float B = -(2*DD*Mathf.Cos(THETA**Mathf.Deg2Rad));//要变换成弧度
float C = DD*DD;
float DELTA = B*B-4*A*C;
if (DELTA>=0){//如果DELTA小于0,无解
float F1 = (-B+Mathf.Sqrt(B*B-4*A*C))/(2*A);
float F2 = (-B-Mathf.Sqrt(B*B-4*A*C))/(2*A);
if(F1<F2)//取较小的一个
F1 = F2;
//命中点位置等于 飞机初始位置加上计算出F边长度乘以飞机前进的方向向量,这个乘法等于把前进的距离变换成世界坐标的位移
hitPoint = aircraft.transform.position + aircraftDirection * F1;
}
假设你的炮弹是个Prefab叫projectilePrefab,带有一个刚体,那么可以这样生成炮弹实例:
if(hitPoint != Vector3.zero){//如果有解
//生成一个炮弹实例,位置在炮塔的位置,方向是从炮塔指向命中点
GameObject obj = (GameObject)Instantiate(projectilePrefab,gun.transform.position,Quaternion.LookRotation(hitPoint));
//假设muzzleVelocity是设定的炮弹速度(0,0,muzzleVelocity)表示往正z方向运动,用TransformDirection把这个速度变换成世界坐标的速度向量
obj.rigidbody.velocity = obj.transform.TransformDirection(new Vector3(0,0,muzzleVelocity));
}
经过以上计算,炮弹可以准确的命中飞行中的目标,只要目标是按照固定速度和方位角飞行的,可以百发百中。当然也会有无解的情况,所以计算的时候判断了Delta,一共也就是几条语句。
2.抛物线弹道
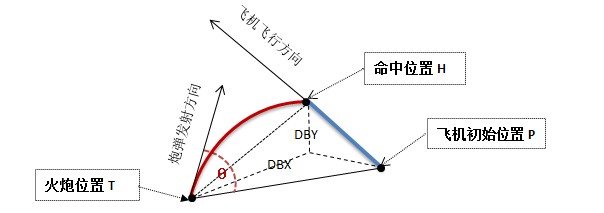
考虑进重力影响,炮弹的弹道就是一个抛物线方程,而目标还是在3D空间的匀速直线运动,一个空间直线方程。
一个曲线方程和一个直线方程,以隐含参数t(飞行时间)求共同解(相交)问题,列方程组:
其中Vp和Vg分别代表飞机和炮弹飞行速度,角度Theta是炮弹射出时的仰角,t是飞行时间。这是个非齐次非线性隐含微分方程组,以某人的数学基础,看不出有什么特殊解的方法,用常规的迭代逼近求解吧,求达人提供更好方法。
迭代的过程大致是:
1.用一组预测的xy落点坐标带入抛物线方程
2.求出发射的角度和飞行时间t
3.将时间带t入直线方程,求出相应的xy坐标
4.将这个坐标与之前猜测的xy坐标进行比较,如果差值小于允许误差,迭代结束返回结果
5.如果差值大于误差,将这个新的xy作为下一次计算的预测xy,返回步骤1
这个过程的物理含义可以这样理解:瞄准飞机现在的位置发射,等炮弹飞到的时候飞机已经往前飞行了一段距离,把炮弹飞行时间乘以飞机速度,得到飞机在该时刻的实际位置,下次瞄准这个位置,再计算,因为目标变了,炮弹的飞行时间也变了,所以该时刻飞机位置也不同了,就这样不停循环,炮弹落点追赶飞机位置,直到两者差距无穷小。
针对抛物线方程把t带入,得到:
然后用基础代数方法进行推导化简,再用通用求根公式得到:
这样θ角就可以通过预测的落点坐标、炮弹初速度、重力加速度g来求出。
迭代是有很多技巧的,这些内容需要复习大学微积分课程。好的迭代方法能够快速收敛,最大化的解释运算开销。望高数达人提供更佳的迭代方法。
在Unity中实现,有几个核心思想:
1.迭代体用函数递归来实现
2.抛物线本身是2D曲线,所以其实不需要3重坐标就能计算,每次运算时把z指向预测的落点,第3个坐标可以无视
3.各种变换可以快速的通过向量、矩阵运算得到,很方便,不需要总是借助transform
//抛物线方程 X Y代表预测落点,V代表炮弹初速,G是重力加速度 返回值是Vector2,其中x是发射角,y是飞行时间
Vector2 formulaProjectile(float X,float Y,float V,float G){
if(G ==0){//如果无重力 问题就成了简单的三角函数 THETA等于atan(y/x) 飞行时间就等于(Y/sin(THETA))(斜边长)再除以速度
float THETA = Mathf.Atan(Y/X);
float T = (Y/Mathf.Sin(THETA))/V;
return(new Vector2(THETA,T));
}else{//用上面的公式进行计算
float DELTA = Mathf.Pow(V,4)-G*(G*X*X-2*Y*V*V);
if(DELTA < 0){//DELTA小于0无解
return Vector2.zero;
}
float THETA1 = Mathf.Atan((-(V*V)+Mathf.Sqrt(DELTA))/(G*X));
float THETA2 = Mathf.Atan((-(V*V)-Mathf.Sqrt(DELTA))/(G*X));
if(THETA1>THETA2)//取较小值
THETA1 = THETA2;
float T = X/(V*Mathf.Cos(THETA1));//用抛物线水平运动方程计算飞行时间 比较简单
return new Vector2(THETA1,T);
}
}
//目标运动的直线方程 VT是目标运动速度 PT是目标当前位置 DT是目标运动方向 TT是运动时间 返回值是目标经过时间TT以后的实际位置
Vector3 formulaTarget(float VT,Vector3 PT,Vector3 DT,float TT){
//简单的一句话搞定直线方程计算 目标实际位置=目标当前位置+目标运动方向向量*(目标飞行速度*目标飞行时间)
return PT + DT * (VT * TT);
}
//主迭代函数 参数灰常多 用于算法演示 实际使用是可以简化的
//gunVelocity:炮弹初速度 gunPosition:炮塔世界坐标 aircraftVelocity:飞机线速度 aircraftPosition:飞机当前位置世界坐标
//aircraftDirection:飞机飞行方向向量 hitPoint:预测的命中点 G:重力加速度 accuracy:计算精度 小于这个值认为计算完成 diff:上次迭代的差值
//返回值是炮塔发射时瞄准点的坐标(注意不是实际命中点)
Vector3 calculateNoneLinearTrajectory(float gunVelocity,Vector3 gunPosition,float aircraftVelocity,
Vector3 aircraftPosition,Vector3 aircraftDirection,Vector3 hitPoint,float G,float accuracy,float diff){
//如果预测命中点是0 无解 返回0
if(hitPoint == Vector3.zero){
return Vector3.zero;
}
//把炮塔正z指向预测命中点在炮塔高度的一个水平面上的投影点
//这样就构造了一个以炮塔为原点,以重力方向为-y轴 以炮塔正前方为x轴的标准抛物线2D坐标系,这个要自己体会下
Vector3 gunDirection = new Vector3(hitPoint.x,gunPosition.y,hitPoint.z) - gunPosition;
//构造一个从世界坐标到炮塔坐标的旋转矩阵
Quaternion gunRotation = Quaternion.FromToRatation(gunDirection,Vector3.forward);
//把预测命中点变换到炮塔坐标(减法是计算相对坐标差,再旋转到炮塔当前坐标来)
Vector3 localHitPoint = gunRotation * (hitPoint - gunPosition);
float V = gunVelocity;
float X = localHitPoint.z;//注视方向 前方是z,也就是抛物线坐标里的X
float Y = localHitPoint.y;
Vector2 TT = formulaProjectile(X,Y,V,G);//用抛物线方程计算射击仰角和飞行时间
if(TT == Vector2.zero){//如果无解 返回
return Vector3.zero;
}
float VT = aircraftVelocity;
Vector3 PT = aircraftPosition;
Vector3 DT = aircraftDirection;
float T = TT.y;//TT的y是用抛物线方程计算出的弹丸飞行时间
Vector3 newHitPoint = formulaTarget(VT,PT,DT,T);//带入直线方程计算目标实际位置 注意目标的计算是在3D世界坐标进行的
float diff1 = (newHitPoint - hitPoint).magnitude;//判断预测点和实际目标位置的距离
if (diff1 > diff){//如果距离大于上一次计算的距离 那么要么迭代算法有问题 是发散的 要么就无解 返回0
return Vector3.zero;
}
if(diff1<accuracy){//如果距离小于希望的精度 找到结果 返回瞄准点 炮弹是抛物线 发射时不能瞄准命中点 要计算瞄准点
gunRotation = Quaternion.Inverse(gunRotation);//把刚才构造的旋转矩阵进行逆变换,从炮塔坐标变回世界坐标
Y = Mathf.Tan(TT.x)*X;//TT的x是炮弹射出的仰角tan(仰角)*水平距离=垂直高度了(三角函数),这才是瞄准点的高度
return gunRotation * new Vector3(0,Y,X) + gunPosition;//把瞄准点变换回世界坐标 注意X其实是Z
}
//即不是无解 也未达到精度要求 递归调用继续迭代 其中预测命中点用目标轨迹方程计算出的新位置取代 参考差值用本次计算的差值取代
return calculateNoneLinearTrajectory(gunVelocity,gunPosition,aircraftVelocity,aircraftPosition,aircraftDirection,newHitPoint,G,accuracy,diff1);
}
一个炮弹运动轨迹方程 一个目标运动轨迹方程,加一个迭代函数,就能完成计算抛物线弹道命中直线匀速移动目标的问题。实际使用的时候,可以先用方法1直线弹道算出一个命中点,作为初始预测点带入进行迭代,可以减少迭代次数。过程里使用了大量简化的向量和矩阵运算,对这部分不熟的读起来可能费劲。
在几千米范围以内的飞机,飞行速度在300-700km/h,炮弹出膛速度在500m/s(2战水平,其实高射炮出膛速度不止这么点),命中精度10m以内的前提下,基本上4次迭代以内可以完成。
3.更多复杂因素的计算
在实际情况中,还可能有更多的影响。比如目标不是匀速直线而是加速运动或者曲线运动,比如空气阻力对弹道的影响,弹丸质心不在几何中心时与重力、空间阻力夹角产生的偏转力矩,炮弹在移动的平台上射击移动的目标。另外炮弹出射点是从炮口算起,在旋转炮塔和炮管的情况下,这个出射点其实是个球面轨迹而不是个固定点。火炮发现目标到炮口转动到合适位置的时间里,目标又发生了位移,所以还要计算这个炮塔旋转的提前量。这一系列的复杂问题其实都可以通过联立方程组,然后迭代求解的方法实现,原理完全一样,只是计算复杂度大大增加。
比如在考虑空气阻力等情况下,炮弹的轨迹方程会是这种形式:
这些影响因素可能是线性的、2次乃至高次的。根据上面的算法,只要把抛物线方程组变成这个新的高次方程组求解,也可以适用。
再比如目标飞行的不是直线而是圆形,那么把目标的方程组变换成圆方程,也可以适用。当然在目标轨迹是非线性轨迹的情况下,迭代就不能用这种线性的迭代了,否则迭代结果会一会收敛一会发散,常规的方法是用目标轨迹函数的导函数计算迭代,这部分实在很难做到通用,需要根据具体情况调整。
给出一个概念方程组:
把这些方程组中按照影响关系进行多次分步迭代,最终能得到合适的解或者判断无解。这组方程可以应对各种复杂情况的组合,实际上军事上火控系统正是这样计算的。不过在游戏中,通常不需要这么复杂的计算,只要简单的模拟就足够了,所以只是从概念层面讨论一下,如果这些复杂因素都考虑进去,完全可以作成一个可视的军事仿真的程序来了。
惯例...只写原理不付DEMO大致是没多少人看的,附上自己写的demo

Reset Target:设置目标飞机以随机方位角和速度飞行
Gravity ON/OFF:设置是否开启重力
Aiming Mode: Manual/Auto 设置瞄准模式人工/自动
人工模式下:wsad键上下左右旋转炮管方位角 空格键击发
自动模式下:炮管自动瞄准提前量瞄准点,空格击发 百发百中
AutoCam ON/OFF:设置飞机小镜头的显示模式,关闭自动镜头可以用按钮调整镜头的角度 + -按钮缩放镜头


Change Focus:改变主镜头焦点,在高射炮和目标飞机之间切换,以飞机为焦点时的镜头:

如果无法命中,会发出提示音效
不同视角下的效果:百发百中的弹道 只给了炮弹一个初速度和方向 然后靠碰撞检测显示爆炸效果,过程完全靠物理引擎控制。




人工发射模式:


设置参数:
速度的单位都是m/s,长度单位都是m
Range是飞机初始位置的范围
Gravity Modifier:重力缩放因子,因为场景和模型是1:10比例,所以重力设置为1/10,否则就像玩具,模拟的效果不会真实
其他参数都会用这个因子缩放,所以按照实际情况设置就行。
可下载相关附件!
感谢网友@hog 的分享。