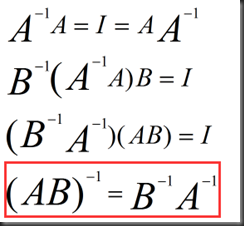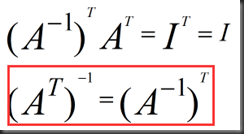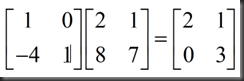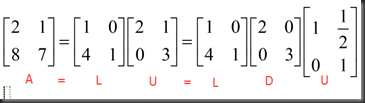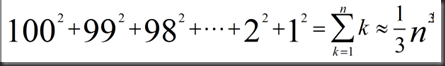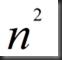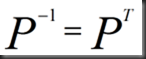Inverse of AB,A^(A的转置)
Product of elimination matrices A=LU (no row exchanges)
Inverse of AB,A^(A的转置):
Product of elimination matrices A=LU (no row exchanges)
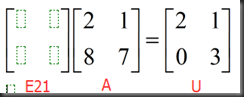
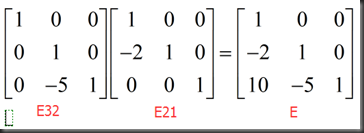
E32E31E21A=U (no row exchanges) EA=U
A=E21`E31`E32`U
L表示下三角矩阵,lower triangle
D表示对角矩阵,diagonal triangle
A=LU
L=E21`E31`E32`
对比EA=U & A=LU,哪种形式更好一些?
example:
设E31为单位矩阵,
A=LU的形式更加简洁一些,if no row exchanges, multipliers go directly into L
思考:How many operations on n * n Matrix(A)? 也就是多少数字改变了?
假设n=100,
row1 不改变,后续行消元,99*100次运算,约看作100*100次;
对第二行进行消元,98*99次运算,约看作99*99次;
继续…
所以总运算次数为
从积分角度考虑可得最终结果
Permutation
考虑单位矩阵的行变换,所有情况一一列出(共6种)
这6个矩阵好像构成了一个群,不论是乘还是逆运算,所得结果均在此群中,且满足条件
若是4维矩阵,则满足条件的、构成群的矩阵有4!=24个
若是n维矩阵,则满足条件的、构成群的矩阵有n!个