BZOJ 3166: [Heoi2013]Alo

Welcome to ALO ( Arithmetic and Logistic Online)。这是一个VR MMORPG ，
如名字所见，到处充满了数学的谜题。
现在你拥有n颗宝石，每颗宝石有一个能量密度，记为ai，这些宝石的能量
密度两两不同。现在你可以选取连续的一些宝石（必须多于一个）进行融合，设为 ai, ai+1, …, a j，则融合而成的宝石的能量密度为这些宝石中能量密度的次大值
与其他任意一颗宝石的能量密度按位异或的值，即，设该段宝石能量密度次大值
为k，则生成的宝石的能量密度为max{k xor ap | ap ≠ k , i ≤ p ≤ j}。
现在你需要知道你怎么选取需要融合的宝石，才能使生成的宝石能量密度最大。

第一行，一个整数 n，表示宝石个数。
第二行， n个整数，分别表示a1至an，表示每颗宝石的能量密度，保证对于i ≠ j有 ai ≠ aj。

输出一行一个整数，表示最大能生成的宝石能量密度。

5
9 2 1 4 7

14

【样例解释】
选择区间[1,5]，最大值为 7 xor 9。
对于 100%的数据有 1 ≤ n ≤ 50000, 0 ≤ ai ≤ 10^9

加强型数据By Hta

分析：

首先我们处理出来对于每一个元素其最大的作为次大值的区间，这样应该左右分别有两个，大概就是下面这张图：

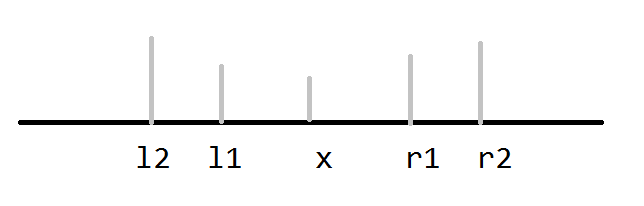
我们可以选择(l1,r2)这个区间，也可以选择(l2,r1)这个区间，但是我们发现其实不用这么麻烦，我们只需要求出(l2,r2)这个区间就可以了，因为我不论选择哪一个位置的元素都可以找到一个合法的区间包含这个位置的元素...

然后维护了区间之后用可持久化Trie树贪心就好了...

然后怎么求合法区间呢？我一开始很YY了一个强行多加一个$log$的$O(Nlog^{2}N)$的做法，什么脑残的$ST$表+二分，被YouSiki嘲讽脑子进水了...然后后来看YouSiki的之前的代码的时候发现这货也用的是$ST$表...哈哈哈，没救了...

其实正确做法很简单，把位置按照权值从大到小排序，用$set$维护，每个x的合法区间就是[x的前驱的前驱+1,x的后继的后继-1]...

代码：

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<set> 
//by NeighThorn
using namespace std;

const int maxn=50000+5,maxm=maxn*32+5;

int n,ans,tot,sum[maxm],nxt[maxm][2],root[maxn];

struct M{
	int x,pos;
}b[maxn];

set<int> s; 
set<int>::iterator itl,itr;

inline bool cmp(M a,M b){
	return a.x>b.x;
}

inline int insert(int x,int val){
	int rt=++tot,y=rt;
	for(int i=30;i>=0;i--){
		nxt[y][0]=nxt[x][0],nxt[y][1]=nxt[x][1];
		sum[y]=sum[x]+1;
		int lala=(val>>i)&1;
		nxt[y][lala]=++tot;
		y=nxt[y][lala];
		x=nxt[x][lala];
	}
	sum[y]=sum[x]+1;
	return rt;
}

inline int query(int l,int r,int val){
	int ans=0;
	for(int i=30;i>=0;i--){
		int lala=((val>>i)&1)^1;
		if(sum[nxt[r][lala]]-sum[nxt[l][lala]]>0)
			ans|=1<<i,l=nxt[l][lala],r=nxt[r][lala];
		else
			l=nxt[l][lala^1],r=nxt[r][lala^1];
	}
	return ans;
}

signed main(void){
	scanf("%d",&n);ans=0;
	for(int i=1;i<=n;i++)
		scanf("%d",&b[i].x),b[i].pos=i,root[i]=insert(root[i-1],b[i].x);
	sort(b+1,b+n+1,cmp);s.insert(b[1].pos);
	s.insert(-1);s.insert(n+1);s.insert(-2);s.insert(n+2);
	for(int i=2;i<=n;i++){
		int l=b[i].pos,r=b[i].pos,pos=b[i].pos;
		s.insert(pos);
		itr=itl=s.lower_bound(pos);
		itr++;r=*itr,itr++;r=*itr-1;
		itl--,l=*itl;itl--,l=*itl+1;
		l=max(1,l),r=min(r,n);
		if(l!=r) ans=max(ans,query(root[l-1],root[r],b[i].x));
	}
	printf("%d
",ans);
	return 0;
}

By NeighThorn

BZOJ 3166: [Heoi2013]Alo

3166: [Heoi2013]Alo

Description

Input

Output

Sample Input

Sample Output

HINT

Source

分析：

代码：