Jump Game II

Date:

　　Nov. 3, 2017

Problem:

　　https://leetcode.com/problems/jump-game-ii/description/

Description:

　　Given an array of non-negative integers, you are initially positioned at the first index of the array.

　　Each element in the array represents your maximum jump length at that position.

　　Your goal is to reach the last index in the minimum number of jumps.

　　For example:

Given array A = [2,3,1,1,4]
The minimum number of jumps to reach the last index is 2. (Jump 1 step from index 0 to 1, then 3 steps to the last index.)

　　Note:
　　You can assume that you can always reach the last index.

　　看到题目，我马上想到了一副非常美丽的交错的备忘搜索树的图景，然后意识到wallpaper engine对我大脑的内存占用还是很高的。

　　很容易画出example的拓扑图：

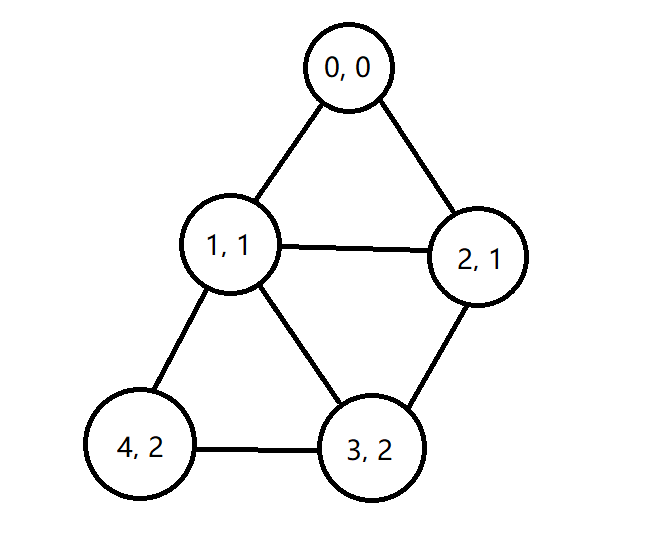
　　每个节点表示数组中的一个位置，节点中有两个值，分别表示位置的索引和到达该位置所需的最小步数。两个节点之间的连线表示可以从索引较小的那个位置走到较大的那个位置。

　　于是思维马上开始发散，想到被开水烫变形的动规表，然后就开始想深搜广搜……

　　不过既然是一道数组题，我就用粗暴一点的方式来做吧。

　　首先设置一个指针pointer，让他指向第0个位置。length，指示最后一个节点的索引。rank，指示pointer遍历至今，我能走到的最远距离。smallest，保存到达每一个走过的位置需要的最小步数。

　　接下来，我用指针i遍历pointer + 1， pointer + 2，...，pointer + nums[pointer]，即我在pointer这个位置能走过的路径，检查smallest[i]是否存在。这可以通过检查rank与遍历指针的大小关系判断。因为，如果smallest[i]不存在，我们接下来就要把smallest[pointer] + 1加入smallest的末尾，然后让rank += 1，由于遍历指针总是从已经走到的位置开始每次间隔为1地向右移动，所以我们总是不用担心在smallest[233]还未录入时，就录入了smallest[666]，同样的，也可以放心地用rank判断接下来的操作到底是录入还是判断替换。

　　反之，当我们检查到smallest[i]存在时，我们研究smallest[i]与我们现在走到这个位置的步数smallest[pointer] + 1的大小关系，保留更小的那个数，将其记录在smalles[i]中。

　　完成了这一步骤后，我令pointer += 1，继续研究下一个节点和它可以走到的那些节点。如此推演，直到pointer到达length - 1。这时，我将smallest[length]输出。

　　这时我想到一个问题。我其实不需要演算rank大于length的部分，万一靠近length的地方有个十个八个的能跳千百万步的，我岂不是死在length门口。因为这一部分计算完全是无用功。所以，我们在指针i遍历的环节加上一个判断条件，仅当i <= length时才进入smallest检查，否则break。

　　这好像有点像那啥，戴克斯特拉算法。复杂度为O(N*N)。

　　提交，TLE。

　　……

　　

　　翻看了一下记录，死在一个[25000, 24999, 24998, ... , 2, 1, 1, 0]。

　　这是要搞事吧？

　　进一步简化smallest查找。事实上，当一个位置的“步长”覆盖了若干个这样的位置，这些位置的“步长”甚至不能超出这个范围，这时，我们完全没有必要扫描这些位置。

            if rank >= pointer > 0 and nums[pointer] <= nums[parent[pointer]] - pointer + parent[pointer]:
                pointer += 1
                continue

　　提交，AC。

　　这种算法的复杂度是O(N)。（

　　以下是submission。

class Solution:
    def jump(self, nums):
        length = len(nums) - 1
        parent = [0]
        smallest = [0]
        rank = 0
        pointer = 0
        while pointer < length:
            if rank >= pointer > 0 and nums[pointer] <= nums[parent[pointer]] - pointer + parent[pointer]:
                pointer += 1
                continue
            for i in range(pointer + 1, pointer + nums[pointer] + 1):
                if i <= length:
                    if rank < i:
                        rank += 1
                        smallest.append(smallest[pointer] + 1)
                        parent.append(pointer)
                    elif smallest[i] > smallest[pointer] + 1:
                        smallest[i] = smallest[pointer] + 1
                        parent[i] = pointer
                else:
                    break
            pointer += 1
        return smallest[length]

　　jianchao.li.fighter优美的BFS算法，step全局记录，复杂度O(N)。

class Solution:
    def jump(self, nums):
        n, start, end, step = len(nums), 0, 0, 0
        while end < n - 1:
            step += 1
            maxend = end + 1
            for i in range(start, end + 1):
                if i + nums[i] >= n - 1:
                    return step
                maxend = max(maxend, i + nums[i])
            start, end = end + 1, maxend
        return step