快速傅里叶变换(FFT)学习笔记

定义

多项式

系数表示法

设(A(x))表示一个(n-1)次多项式，则所有项的系数组成的(n)维向量((a_0,a_1,a_2,dots,a_{n-1}))唯一确定了这个多项式。

即

[A(x)=sum limits_{i=0}^{n-1}a_ix^i ]

[=a_0+a_1x+a_2x^2+dots+a_{n-1}x^{n-1} ]

点值表示法

将(n)个互不相同的(x)代入多项式，会得到(n)个互不相同的取值(y)。设他们组成的(n)维向量分别为((x_0,x_1,x_2,dots,x_{n-1}),(y_0,y_1,y_2,dots,y_{n-1}))。则给多项式被这两个(n)维向量唯一确定。

其中

[y_i=A(x_i)=sum limits_{j=0}^{n-1}a_j imes x_i^j ]

多项式乘法

定义两个多项式(A(x)=sumlimits_{i=0}^{n-1}a_ix^i)与(B(x)=sumlimits_{i=0}^{n-1}b_ix^i)相乘的结果为(C(x))。

则

(C(x)=A(x) imes B(x)=sumlimits_{k=0}^{2n-2}(sum limits_{k=i+j} a_ib_j)x^k)

形如(C(k)=sum limits_{ioplus j=k}a_ib_j)的式子称为卷积，注意到，多项式乘法的本质就是加法卷积。

两个(n-1)次多项式相乘，得到的是一个(2n-2)次多项式，时间复杂度为(O(n^2))。

若取两个多项式在(2n-1)个点处的点值表示，则

[{y_3}_i=(sumlimits_{j=0}^{2n-2}a_jx_i^j) imes(sumlimits_{j=0}^{2n-2}b_jx_i^j)={y_1}_i imes{y_2}_i ]

复数

设(a,b)为实数，(i^2=-1)，形如(a+bi)的数叫做复数，其中(i)被称为虚数单位。复数域是已知最大的域。

复平面

在复平面中，(x)轴代表实数，(y)轴代表虚数。每一个复数对应复平面上一个从((0,0))指向((a,b))的向量。

向量的长度(sqrt{a^2+b^2})叫做模长。表示从(x)轴正半轴到该向量的转角的有向角叫做幅角。

运算法则

记(z_1=(a,b),z_2=(c,d))。

复数相加遵循平行四边形法则。(z_1+z_2=(a+c,b+d))。

复数相乘时，模长相乘，幅角相加。(z_1 imes z_2=(ac-bd,ad+bc))。

单位根

定义

下文中，默认(n)为2的正整数次幂。

在复平面上以原点为圆心，(1)为半径作圆，所得的圆叫单位圆。以原点为起点，圆的的(n)等分点为终点，作(n)个向量，设幅角为正且最小的向量对应的复数为(omega_n)，则称(omega_n)为(n)次单位根。

由复数的乘法定义（模长相乘，幅角相加）可知，其余的(n-1)个向量对应的复数分别为(omega_n^2,omega_n^3,dots,omega_n^n)，且易知(omega_n^0=omega_n^n=1)。

那么如何计算他们的值呢？

欧拉公式解决了这个问题：

[omega_n^k=cos kfrac{2pi}{n}+ isin kfrac{2pi}{n} ]

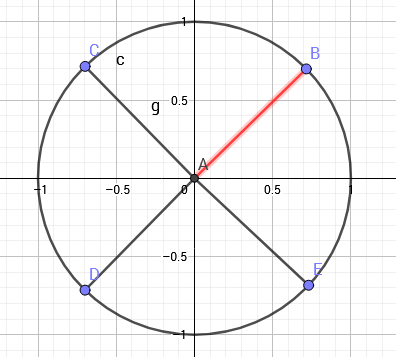
如图，向量(overrightarrow{AB})表示的复数为(8)次单位根，单位根的幅角为(frac{pi}{n})

代数中，若(z^n=1)，则称(z)为(n)次单位根。

性质

• (omega_n^k=cos kfrac{2pi}{n}+ isin kfrac{2pi}{n})

• (omega_{2n}^{2k}=omega_n^k)

从几何意义上来说，在复平面上，二者表示的向量终点相同。

证明：

[omega_{2n}^{2k}=cos 2k frac{2pi}{2n}+isin 2kfrac{2pi}{2n}=cos kfrac{2pi}{n}+ isin kfrac{2pi}{n}=omega_n^k ]

• (omega_{n}^{k+frac{n}{2}}=-omega_n^k)

证明：

[omega_n^{frac{n}{2}}=cos frac{n}{2} cdot frac{2pi}{n}+ isin frac{n}{2} cdot frac{2pi}{n}=cos pi+isin pi=-1 ]

[omega_{n}^{k+frac{n}{2}}=omega_n^k imesomega_n^{frac{n}{2}}=-omega_n^k ]

• (omega_n^0=omega_n^n=1)

快速傅里叶变换(FFT)

前面提到过，一个(n-1)次多项式可以被(n)个点唯一确定。

考虑多项式(A(x))的表示。将(n)次单位根的(0)到(n-1)次幂代入多项式的系数表示，所得点值向量((A(omega_n^0),A(omega_n^1),dots,A(omega_n^{n-1})))称为其系数向量((a_0,a_1,dots,a_{n-1}))的离散傅里叶变换。

但是按照朴素算法求离散傅里叶变换，时间复杂度仍然是(O(n^2))。

[A(x)=a_0+a_1x+a_2x^2+a_3x^3+dots+a_{n-1}x^{n-1} ]

考虑将多项式按照系数下标的奇偶分为两部分

[A(x)=(a_0+a_2x^2+a_4x^4+dots+a_{n-2}x^{n-2})+(a_1x+a_3x^3+a_5x^5+dots+a_{n-1}x^{n-1}) ]

设

[A_1(x)=a_0+a_2x+a_4x^2+dots+a_{n-2}x^{frac{n}{2}-1} ]

[A_2(x)=a_1+a_3x+a_5x^2+dots+a_{n-1}x^{frac{n}{2}-1} ]

则有

[A(x)=A_1(x^2)+xA_2(x^2) ]

假设(k<frac{n}{2})，那么现在要求(A(omega_n^k))

[A(omega_n^k)=A_1(omega_n^{2k})+omega_n^kA_2(omega_n^{2k}) ]

[=A_1(omega_{frac{n}{2}}^{k})+omega_n^kA_2(omega_{frac{n}{2}}^{k}) ]

对于(A(omega_n^{k+frac{n}{2}}))

[A(omega_n^{k+frac{n}{2}})=A_1(omega_n^{2k+n})+omega_n^{k+frac{n}{2}}A_2(omega_n^{2k+n}) ]

[=A_1(omega_n^{2k} imesomega_n^n)-omega_n^kA_2(omega_n^{2k} imesomega_n^n) ]

[=A_1(omega_n^{2k})-omega_n^kA_2(omega_n^{2k}) ]

[=A_1(omega_{frac{n}{2}}^{k})-omega_n^kA_2(omega_{frac{n}{2}}^{k}) ]

神奇的事情发生了！注意到，当(k)取遍([0,frac{n}{2}-1])时，(k)和(k+frac{n}{2})取遍了([0,n-1])。

这也就意味着，如果我们已经知道了(A_1(x))和(A_2(x))在(omega_{frac{n}{2}}^0,omega_{frac{n}{2}}^1,dots,omega_{frac{n}{2}}^{frac{n}{2}-1})处的取值，那么我们就可以在(O(n))的时间内求得(A(x))在(omega_n^0,omega_n^1,dots,omega_n^{n-1})处的取值。而关于(A_1(x),A_2(x))的问题又都是相对原问题规模缩小了一半的子问题，所以只要不断的分治下去，而分治的边界就是一个常数项(a_0)。

该算法的时间复杂度为

[T(n)=2T(n/2)+O(n)=O(nlog n) ]

这就是最常用的(FFT)算法——(Cooley-Tukey)算法。

快速傅里叶逆变换(IFFT)

上面的讨论都是基于点值表示法的，但是在平时的应用中，很少用点值表示法来表示一个多项式。所以考虑将点值表示的多项式转化为系数表示，这个过程同样可以使用快速傅里叶变换，称为傅里叶逆变换。

设((y_0,y_1,y_2,dots,y_{n-1}))为((a_0,a_1,a_2,dots,a_{n-1}))的傅里叶变换（即点值表示），设有另一个向量((c_0,c_1,c_2,dots,c_{n-1}))满足

[c_k=sum limits_{i=0}^{n-1}y_i(omega_n^{-k})^i ]

即多项式(B(x)=y_0+y_1x+y_2x^2+dots+y_{n-1}x^{n-1})在(omega_n^0,omega_n^{-1},omega_n^{-2},dots,omega_n^{-(n-1)})处的点值表示。

下面就是推柿子时间，将上式展开，得到

[c_k=sumlimits_{i=0}^{n-1}y_i(omega_n^{-k})^i ]

[=sumlimits_{i=0}^{n-1}(sum limits_{j=0}^{n-1} a_j(omega_n^i)^j)(omega_n^{-k})^i ]

[=sumlimits_{i=0}^{n-1}(sum limits_{j=0}^{n-1} a_j(omega_n^j)^i)(omega_n^{-k})^i ]

[=sumlimits_{i=0}^{n-1}(sum limits_{j=0}^{n-1} a_j(omega_n^j)^i(omega_n^{-k})^i) ]

[=sumlimits_{i=0}^{n-1}sum limits_{j=0}^{n-1} a_j(omega_n^{j-k})^i ]

[=sum limits_{j=0}^{n-1} a_j(sumlimits_{i=0}^{n-1}(omega_n^{j-k})^i) ]

设(S(x)=sum limits_{i=0}^{n-1}x^i)

将(omega_n^k)代入得

(S(omega_n^k)=1+omega_n^k+(omega_n^k)^2+dots+(omega_n^k)^{n-1})

当(k eq0)时，两边同时乘上(omega_n^k)，得

(omega_n^kS(omega_n^k)=omega_n^k+(omega_n^k)^2+(omega_n^k)^3+dots+(omega_n^k)^n)

两边相减，整理后得到

[omega_n^kS(omega_n^k)-S(omega_n^k)=(omega_n^k)^n-1 ]

[S(omega_n^k)=frac{(omega_n^k)^n-1}{omega_n^k-1} ]

分子为(0)，分母不为(0)，所以

[S(omega_n^k)=0 ]

当(k=0)时，显然(S(omega_n^k)=1)

继续考虑上面的柿子

[c_k=sum limits_{j=0}^{n-1} a_j(sumlimits_{i=0}^{n-1}(omega_n^{j-k})^i) ]

[=sum limits_{j=0}^{n-1} a_jS(omega_n^{j-k}) ]

当(j=k)时，(S(omega_n^{j-k})=n)，否则(S(omega_n^{j-k})=0)，即

[c_i=na_i ]

[a_i=frac{1}{n}c_i ]

所以，使用单位根的倒数代替单位根，再做一次类似快速傅里叶变换的过程，最后将所得的每个数除以(n)，即为傅里叶逆变换的结果。

代码实现

递归实现

递归实现直接参照上面的结论来进行实现即可，比较直观。

需要注意的是，不要使用(STL)里的(complex)类，会被卡常数。

代码

#include <bits/stdc++.h>
using namespace std;

inline int ty() {
	char ch = getchar(); int x = 0, f = 1;
	while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }
	while (ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }
	return x * f;
}

const int _ = 4e6 + 10;
const double Pi = acos(-1.0);
struct Complex {
	double x, y;
	Complex(double _x = 0, double _y = 0) { x = _x, y = _y; }
	Complex operator+(const Complex &b) const { return Complex((double)x + b.x, (double)y + b.y); }
	Complex operator-(const Complex &b) const { return Complex((double)x - b.x, (double)y - b.y); }
	Complex operator*(const Complex &b) const { return Complex((double)x * b.x - (double)y * b.y, (double)x * b.y + (double)y * b.x); }
} a[_], b[_];
int N, M;

void fft(int lim, Complex *a, int op) {
	if (lim == 1) return;
	Complex a1[(lim >> 1) + 5], a2[(lim >> 1) + 5];
	for (int i = 0; i < lim; i += 2)
		a1[i >> 1] = a[i], a2[i >> 1] = a[i + 1];
	fft(lim >> 1, a1, op);
	fft(lim >> 1, a2, op);
	Complex Wn = Complex(cos(2.0 * Pi / lim), op * sin(2.0 * Pi / lim)); // 单位根
	Complex w = Complex(1, 0);
	for (int i = 0; i < (lim >> 1); ++i, w = w * Wn) {
		a[i] = a1[i] + w * a2[i];
		a[i + (lim >> 1)] = a1[i] - w * a2[i];
	}
}

int main() {
#ifndef ONLINE_JUDGE
	freopen("fft.in", "r", stdin);
	freopen("fft.out", "w", stdout);
#endif
	N = ty(), M = ty();
	for (int i = 0; i <= N; ++i) a[i].x = ty();
	for (int i = 0; i <= M; ++i) b[i].x = ty();
	int lim = 1; while (lim <= N + M) lim <<= 1;
	fft(lim, a, 1);
	fft(lim, b, 1);
	for (int i = 0; i <= lim; ++i) a[i] = a[i] * b[i];
	fft(lim, a, -1);
	for (int i = 0; i <= N + M; ++i) printf("%d ", (int)(a[i].x / lim + 0.5));
	return 0;
}

迭代实现

递归实现的(FFT)效率不高，实际当中一般用迭代实现。

二进制翻转

考虑递归 FFT 分治到边界时，每个数的顺序，及其二进制位。

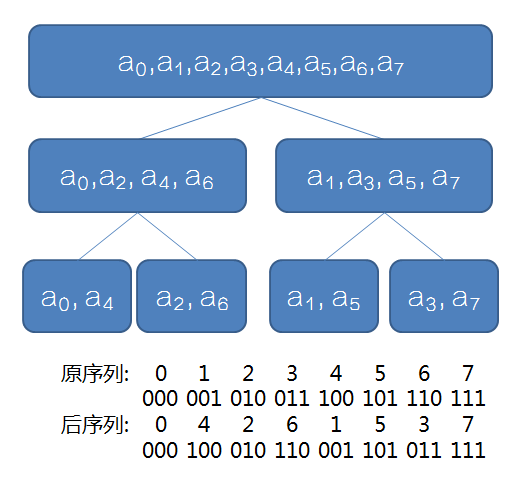
观察一下原序列和翻转后序列的联系，可以发现翻转后的序列下标其实就是原序列下标的二进制翻转。

因此对下标进行奇偶性分类其实是没有必要的，只需要(O(n))求出翻转后的序列，然后不断进行向上合并即可。

蝴蝶操作

具体见代码。

代码

#include <bits/stdc++.h>
using namespace std;

inline int ty() {
	char ch = getchar(); int x = 0, f = 1;
	while (ch < '0' || ch > '9') { if (ch == '-') f = -1; ch = getchar(); }
	while (ch >= '0' && ch <= '9') { x = x * 10 + ch - '0'; ch = getchar(); }
	return x * f;
}

const int _ = 4e6 + 10;
const double Pi = acos(-1.0);
struct Complex {
	double x, y;
	Complex operator+(const Complex &b) const { return {x + b.x, y + b.y}; }
	Complex operator-(const Complex &b) const { return {x - b.x, y - b.y}; }
	Complex operator*(const Complex &b) const { return {x * b.x - y * b.y, x * b.y + y * b.x}; }
} a[_], b[_];
int N, M, pos[_];

void fft(const int lim, Complex *a, int op) {
	for (int i = 0; i < lim; ++i)
		if (i < pos[i]) swap(a[i], a[pos[i]]);
	for (int len = 2; len <= lim; len <<= 1) {
		int mid = len >> 1;
		Complex Wn = {cos(2.0 * Pi / len), op * sin(2.0 * Pi / len)};
		for (int i = 0; i < lim; i += len) {
			Complex w = {1, 0};
			for (int j = 0; j < mid; ++j, w = w * Wn) {
				Complex x = a[i + j], y = w * a[i + j + mid];
				a[i + j] = x + y;
				a[i + j + mid] = x - y;
			}
		}
	}
}

int main() {
#ifndef ONLINE_JUDGE
	freopen("fft.in", "r", stdin);
	freopen("fft.out", "w", stdout);
#endif
	N = ty(), M = ty();
	for (int i = 0; i <= N; ++i) a[i].x = ty();
	for (int i = 0; i <= M; ++i) b[i].x = ty();
	int k = 0, lim = 1;
	while (lim <= N + M) lim <<= 1, ++k;
	for (int i = 0; i < lim; ++i) pos[i] = (pos[i >> 1] >> 1) | ((i & 1) << (k - 1));
	fft(lim, a, 1);
	fft(lim, b, 1);
	for (int i = 0; i <= lim; ++i) a[i] = a[i] * b[i];
	fft(lim, a, -1);
	for (int i = 0; i <= N + M; ++i) printf("%d ", (int)(a[i].x / lim + 0.5));
	return 0;
}

参考资料

FFT 学习笔记 | Menci's Blog

快速傅里叶变换(FFT)详解

[学习笔记&教程] 信号, 集合, 多项式, 以及各种卷积性变换 (FFT,NTT,FWT,FMT) - rvalue - 博客园

如何通俗地解释欧拉公式（e^πi+1=0）？

复数（数的概念扩展）_百度百科