回文自动机[学习笔记]

回文自动机一一处理回文串问题的有力武器

这几天一直沉迷字符串数据结构

看了很多大佬的回文自动机学习笔记，稍微有点理解了，整理一下吧

1.概念

(quad)a.大概： 同其他自动机一样，回文自动机是个DAG，它用相当少（(O(n))）的空间复杂度就存储了这个字符串的所有回文串信息。一个回文自动机包含不超过(|S|)个节点，每个节点都表示了这个字符串的一个不重复的回文子串，同时一个节点会有不超过字符集大小的边连向其他节点，以及一条fail边连向这个点的fail...这些都会在下面介绍

(quad)b.森林： 和别的自动机不太一样，回文自动机是有两棵树的森林：其中一棵是长度为偶数的回文串集合，另一棵是长度为奇数的回文串集合，这两棵树的根节点分别表示长度为0（空串）和-1（无实际含义，便于运算）的回文串;

(quad)c.边：自动机中每条有向边都有一个字符类型的权值，起点的串左右分别加上这个字符得到的就是终点的串。举个栗子：设一条边权为(c)的边连接的两个点分别是(A,B)，(A)表示回文串(aba)，则(B)表示的回文串就是(cabac) 。特别的，如果(A)是那个长度为(-1)的根，(B)串就是这条边的权值。。。

(quad)d.点：当你插入一个字符的时候，插入的点代表的就是这个字符匹配的最长回文串，也就是说从根节点往下顺着边走，记着一个str一开始为空，一边走一边不停地往str左右两边添加新的字符，走到一个点，这个点代表的回文串就是str

(quad)e.(fail)边：每个点都有个fail边，这条边指向这个点所代表的回文串的 最长回文后缀 所在的那个点（最长回文后缀：串中满足回文的最长的后缀，这个串自己不算）如果没有，则指向0（就是那个根节点）。特别的，0的fail节点就是那个长度为-1的点。

2.构造：

(quad)我是用的一个结构体存的，(len,fail,son[26],siz) 分别代表这个串的长，fail节点，连出来的每一条边以及这个回文串的数量，如下

struct node{
	int len,fail,son[26],siz;
};
node prt[maxn]; 

我们把两个根下标设为0和1，并根据上面介绍的给他们赋值

	prt[1].len=-1;
	prt[0].fail=prt[1].fail=1;

然后我们就可以把点一个一个加入到回文自动机中，这可以用一个函数(extend)来实现，具体实现方法如下：

设我们以前插入的最后一个点为(last)，这次要插入一个点x，首先要找到一个点(cur)为满足前面的字符等于新加入字符的，(last)的最长的回文后缀，这个过程可以不停地在(last)的(fail)链上跑，因为(fail)所对应的正是串的最长回文后缀，这个可以用下面函数实现：

int getfail(int x){
	while(s[n-prt[x].len-1]!=s[n]) x=prt[x].fail;
	return x;
}

若(cur)已经包含权值为x的出边了，我们就可以简单地将出边终点的权值++，继续去加下一个点了。如果不包含权值x的边，我们就需要新建一个点(now)并让(cur)把边连向他，(now)代表的长度自然是(cur)的长度+2，然后我们只要求出(now)的(fail)就完事了。

求(fail)的话可以用cur的(fail)来求，就用上面求(cur)的方法，但是不能用(cur)本身（想一想，为什么）

当然最后千万不要忘记把(last)的值更新啊(qwq)

void extend(int x){
	int cur=getfail(last);
	int now=prt[cur].son[x];
	if(!now){
		now=++num;
		prt[now].len=prt[cur].len+2;
		prt[now].fail=prt[getfail(prt[cur].fail)].son[x];
		prt[cur].son[x]=now;
	}
	prt[now].siz++;
	last=now;
}

累计答案可以从下往上把回文串数目加起来，显然上面的串一定是下面串的子串嘛(qwq)

void count(){
	for(int i=num;i>=2;i--)
		prt[prt[i].fail].siz+=prt[i].siz;
}

4.举个栗子：

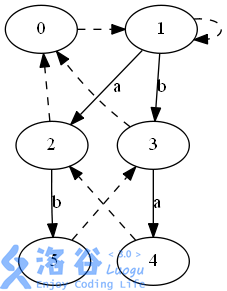
如图，我们已经把串(abab)的回文自动机建好了，下面要添加一个点(a)，此时(last=5)

首先求出(cur)，(last)所代表的回文串(bab)前边的字符正好与要加入的字符(a)相等，所以(cur)就是(last)，我们发现(cur)不存在边权为(a)的出边，于是新建个点 6，从(cur)连一条边(a)到 6；

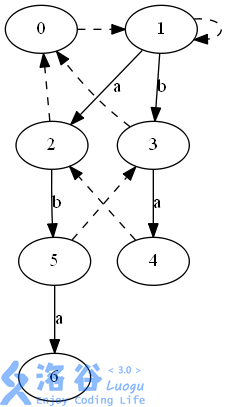
6 的长度自然是5的长度+2((a'bab'a))

然后求6的(last)：5的(fail)指向3((b))，可以发现，3前面的那个字符(a)就是新加的字符（怎么那么巧...），于是我们把6的fail指向点3的(a)边所指向的点4;

嗯，(last)更新为6，6的数量++，结束；

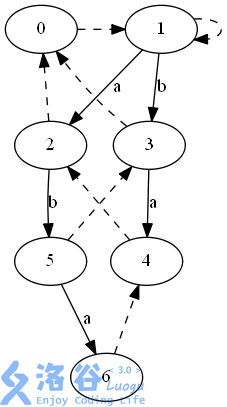
最后累加答案，

(siz(6)=1)，(siz(4)=1)

(siz(5)=1)

((siz(4)+=siz(6))=2)

((siz(3)+=siz(5))=2)

((siz(2)+=siz(4))=3)

附：闲得自己也写了个造图的代码。。。

void print(int x){
	if(cz[x]) return;
	cz[x]=1;
	printf("	%d->%d[style="dashed"];
",x,sam[x].link);
	for(int i=0;i<=25;i++)
		if(sam[x].ch.count(i))
			printf("	%d->%d[label=%d];
",x,sam[x].ch[i],i),
			print(sam[x].ch[i]);
}
void Vz(){
	printf("digraph zhy{
	rankdir = LR;
");
	print(0);
	printf("}
");
}

5.例题（Luogu-1659）：

(quad)这道题的话就是把这些点按照长度从大到小排一遍序，然后前(k)个奇数长的乘起来就是答案啦，注意这题k较大，还要用快速幂，代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn=1e6+100,P=19930726;
struct node{
	int len,fail,son[26],siz;
	node(){
		len=fail=0;
		for(int i=0;i<=25;i++)
			son[i]=0;
	}
};
node prt[maxn]; 
int n,last,len,num;
ll ans=1,k;
char s[maxn];
ll poww(ll x,int y){
	ll base=1;
	while(y){
		if(y&1) base*=x,base%=P;
		x*=x,x%=P;
		y>>=1;
	}
	return base;
}
bool cmp(node x,node y){
	return x.len>y.len;
}
int getfail(int x){
	while(s[n-prt[x].len-1]!=s[n]) x=prt[x].fail;
	return x;
}
void extend(int x){
	int cur=getfail(last);
	if(!prt[cur].son[x]){
		int now=++num;
		prt[now].len=prt[cur].len+2;
		prt[now].fail=prt[getfail(prt[cur].fail)].son[x];
		prt[cur].son[x]=now;
	}
	prt[prt[cur].son[x]].siz++;
	last=prt[cur].son[x];
}
int main(){
	scanf("%d%d",&len,&k);
	scanf("%s",s);
	last=num=1,prt[1].len=-1;
	prt[0].fail=prt[1].fail=1;
	for(n=0;n<len;n++) extend(s[n]-'a');
	for(int i=num;i>=2;i--)
		prt[prt[i].fail].siz+=prt[i].siz,prt[prt[i].fail].siz%=P;
	sort(prt+1,prt+num+1,cmp);
	int now=1;
	while(k){
		if(now>num){
			printf("-1
");
			return 0;
		}
		if(prt[now].len%2==0){
			now++;
			continue;
		}
		if(prt[now].siz<k){
			k-=prt[now].siz;
			ans*=poww(prt[now].len,prt[now].siz)%P;
			ans%=P;
			now++;
		}
		else{
			ans*=poww(prt[now].len,k)%P;
			ans%=P;
			k=0;
		}
	}
	printf("%lld
",ans);
}