圆方树&广义圆方树[学习笔记]

仙人掌

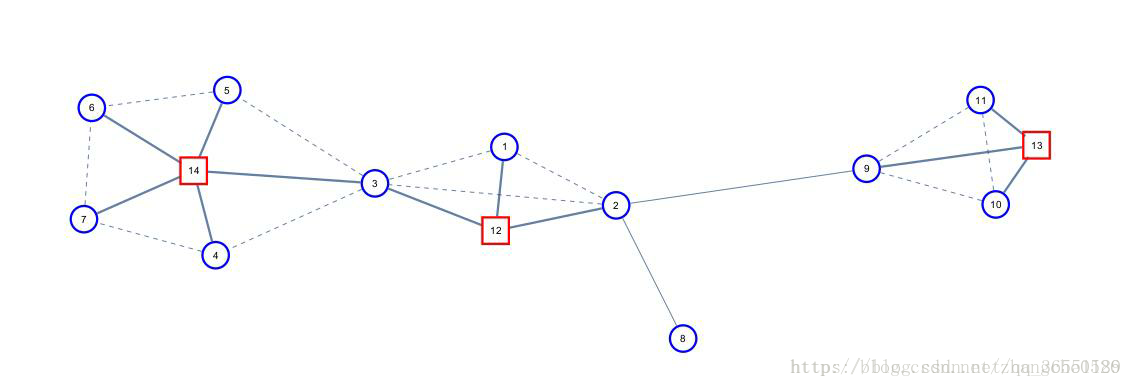
圆方树是用来解决仙人掌图的问题的，那什么是仙人掌图呢？

如图，不存在边同时属于多个环的无向连通图是一棵仙人掌

---

---

圆方树

定义

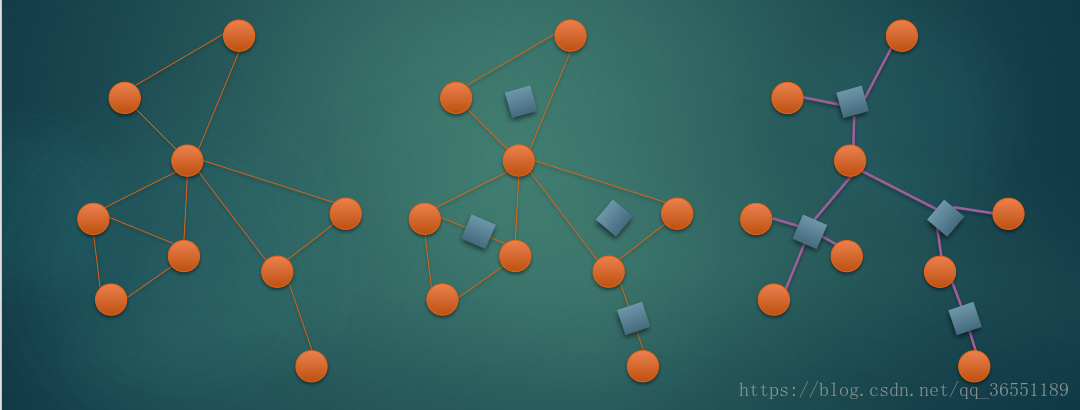
原先的仙人掌图，通过一些奇妙的方法，可以转化为一棵由圆点，方点和树边构成的树——圆方树，具体构建方法如下

原仙人掌的每一个点为圆点，对于每个环都新建一个方点，方点向环上的每一个圆点连边，就构成了圆方树。

---

构建方法

用(tarjan)算法求出点双，对于每一个点双新建一个方点与环上的点相连，注意一条边连接两个点的不算点双。

代码：

void tarjan(int x,int f){
    dfn[x]=low[x]=++tim;
    st[++tot]=x;
    for(int i=G.head[x];i;i=G.nex[i])
        if(G.v[i]!=f){
            int y=G.v[i];
            if(!dfn[y]){
                tarjan(y,x);
                low[x]=min(low[x],low[y]);
                if(low[y]==dfn[x]){
                    siz++;
                    while(st[tot]!=y)
                        T.add(n+siz,st[tot--]);
                    T.add(n+siz,st[tot--]);
                    T.add(n+siz,x);
                }
            }
            else
            if(y!=f)
                low[x]=min(low[x],dfn[y]);
        }
}

---

在别人的博客里学到了一种更妙的构造方法：

记(ring[i])表示点i是否在一个环里。对于某个点x，我们要从它遍历到它的子节点y时，先将(ring[x])赋为0；然后，我们在(tarjan)的时候，若有某个点x，对于其一条连向点y的出边，满足(dfn[y]<dfn[x])，则表明y为其祖先，我们就找到了一个环，于是建方点、连新边，并使该环中每个节点的(ring)变为1；于是，回溯回那个点(x)，若(ring)依然(=0)，则表明那个y没有与之形成环，故边((x,y))是树边，在(T)中连上它。

以及构造的代码：

void tarjan(int x){
    dfn[x]=++tim;
	for(int i=G.head[x];i;i=G.nex[i])
		if(f[x]!=G.v[i]){
			int y=G.v[i];
			if(dfn[y]){
				f[y]=x;
				ring[x]=0;
				tarjan(y);
				if(!ring[x]) T.add(x,y);
			}
			else
				if(dfn[y]<dfn[x]){
					int z=x;
					tot++;
					while(z!=y){
						T.add(z,tot);
						ring[z]=1;
						z=f[z];
					}
					T.add(tot,y);
					ring[y]=1;
				}
		} 
}

---

---

广义圆方树

普通圆方树只能解决仙人掌图上的问题，而广义圆方树则可以将所有无向图转化为圆方树处理。

广义圆方树性质：圆点方点相间，不存在两个‘’相同形状‘’的点相连。

构造方法：

把一条边连接两个点也看成一个点双，原本两个圆点有一条边相连，现在在中间插入一个方点间隔开就好了

（从别人blog搞来的图片）

代码

void tarjan(int x,int f){
    dfn[x]=low[x]=++tim;
    st[++tot]=x;
    for(int i=G.head[x];i;i=G.nex[i])
        if(G.v[i]!=f){
            int y=G.v[i];
            if(!dfn[y]){
                tarjan(y,x);
                low[x]=min(low[x],low[y]);
                if(low[y]>=dfn[x]){
                    siz++;
                    while(st[tot]!=y)
                        T.add(n+siz,st[tot--]);
                    T.add(n+siz,st[tot--]);
                    T.add(n+siz,x);
                }
            }
            else
                low[x]=min(low[x],dfn[y]);
        }
}

---

---

例题

Luogu 4320

比较晚了，先整理这些，以后再补吧