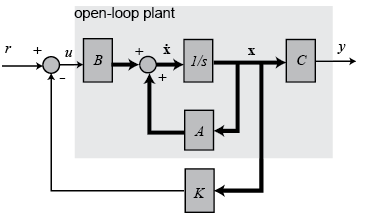
新的“A”变成着了这样:Ac = A - KB
基于对象:状态空间形式的系统
能量函数J:也称之为目标函数
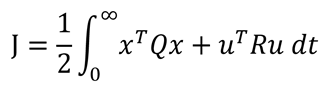
Q:半正定矩阵,对角阵(允许对角元素出现0)
R:正定矩阵,QR其实就是权重
下面这段话可能会加深对LQR的理解:
当x是一维的,J就变成
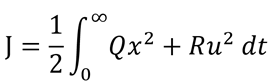
我们的目的是使能量函数J最小,那么Qx^2和Ru^2都要最小,则t趋近无穷时,x要趋近0,要保证Qx^2为一个最小定值那么Q要很大,Q越大x衰减速度也就越快;同理增大R,u就会变小,对系统的控制变弱,x衰减速度将会变慢
如何选取QR?
无一般规律可寻,一般取决设计者的经验,在这提供几个选择的原则:
1 Q、R都是对称矩阵,Q为正半定矩阵,R为正定矩阵
2 通常选取Q、R为对角矩阵,实际应用,通常将R值固定,通过改变Q的值来调制最优,当控制量只有一个,R就变成一个标量,一般取值1
为了更好的选取Q/R,我进行了一些尝试,发现如下:
假设我们的状态量是x1,x2,现在改变系数,观察对x1的影响
关于Q与R的
1 同时Q=>kQ,R=>kr,对x1无影响;
2 单取Q=>kQ或R=>R/k,产生的影响相同;
3 增大Q,对x1的控制力加强;
关于Q内部的
1 增大x1的系数,对x1的控制力加强;
2 增大x2的系数,x1基本不变;
3 减小x2的系数,对x1控制力减弱,以至到达目标状态的时间变长;(试验中对x1的第一步控制较强,但之后控制力明显减弱,可能是由于我给的初始量不太符合客观现实)
计算反馈矩阵K的步骤:
1 选择QR矩阵
2 求解Riccati方程的P(P是公式推导过程中设的矩阵,目的就是方便求K,在这求出P就能求出K)
3 计算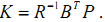 (在matlab中给定A,B,Q,R用lqr函数可直接计算出K)
(在matlab中给定A,B,Q,R用lqr函数可直接计算出K)
(实际控制中我们无法调用lqr函数,求解K本质上属于求解Riccati方程,详见我的随笔:Riccati方程迭代法求解)
u(k)=-K*x(k),u(k)控制完将会得到一个新的x(k+1),周而复始可不断求出u
调节目标:将状态调节到零,而不是系统误差为零
下面有一个倒立摆控制器的例子
其状态变量是[p p' Θ Θ‘],p是小车位移。Θ是倒立摆角度
A = [0 1 0 0
0 0 -1 0
0 0 0 1
0 0 9 0];
B = [0;0.1;0;-0.1];
C = [0 0 1 0]; %观测角度
D = 0;
Q = [1 0 0 0
0 1 0 0
0 0 10 0
0 0 0 10 ];
R = 0.1;
%由上面这个系统,可以计算出K
K = lqr(A,B,Q,R);
Ac = A - B*K;
%对系统进行模拟
x0 = [0.1;0;0.1;0]; %初始状态
t = 0:0.05:20;
u = zeros(size(t));
[y,x]=lsim(Ac,B,C,D,u,t,x0);
plot(t,y);
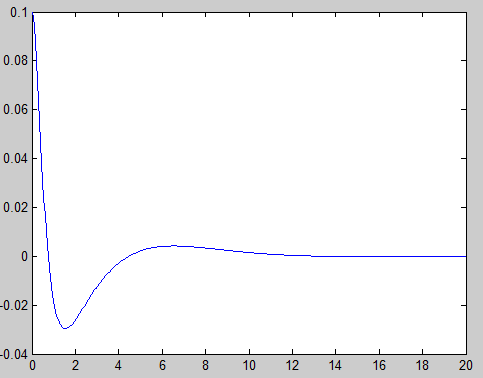
系统的控制效果与系统状态空间的准确度、QR的选取有极大关系!!!
也可采用u(k+1) = -K_lqr * x(k)和x(k+1) = A * x(k) + B * u的方式尝试跑自己的例子