Codeforces Round #287 (Div. 2) D. The Maths Lecture [数位dp]

传送门

D. The Maths Lecture

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Amr doesn't like Maths as he finds it really boring, so he usually sleeps in Maths lectures. But one day the teacher suspected that Amr is sleeping and asked him a question to make sure he wasn't.

First he gave Amr two positive integers n and k. Then he asked Amr, how many integer numbers x > 0 exist such that:

• Decimal representation of x (without leading zeroes) consists of exactly n digits;
• There exists some integer y > 0 such that:
  • ;
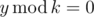  • decimal representation of y is a suffix of decimal representation of x.

As the answer to this question may be pretty huge the teacher asked Amr to output only its remainder modulo a number m.

Can you help Amr escape this embarrassing situation?

Input

Input consists of three integers n, k, m (1 ≤ n ≤ 1000, 1 ≤ k ≤ 100, 1 ≤ m ≤ 109).

Output

Print the required number modulo m.

Sample test(s)

input

1 2 1000

output

4

input

2 2 1000

output

45

input

5 3 1103

output

590

Note

A suffix of a string S is a non-empty string that can be obtained by removing some number (possibly, zero) of first characters from S

题解转自：http://blog.csdn.net/xu12110501127/article/details/43118157

D，数位dp，当时读题的时候读错了。题意是n位的数字，如果存在他的后缀%k=0，就算一种，求出总数来再mod m 就是结果。dp[i][j][k],代表第i位余数为j时他是否已经存在后缀串整除了，0代表不存在，1代表存在。

自己用dp[i][j]做了半天，一直wa，后来看了题解反应过来了，k标志位很关键，既让思路清晰，又避免了 0xxx但是 %k==0这种特殊情况的遗漏，dp水还是很深，要好好练啊~~

#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
#include<map>
#include<set>
#include<stack>
#include<string>

#define N 105
#define M 105
#define mod 1000000007
//#define p 10000007
#define mod2 1000000000
#define ll long long
#define LL long long
#define eps 1e-6
#define inf 1000000
#define maxi(a,b) (a)>(b)? (a) : (b)
#define mini(a,b) (a)<(b)? (a) : (b)

using namespace std;

ll n,k,m;
ll ans;
ll cnt[N*10][N][5];

void ini()
{
    ans=0;
    memset(cnt,0,sizeof(cnt));
}

ll quickpow(ll x,ll nn)
{
    ll re=1;
    while(nn)
    {
        if(nn&1){
            re=(re*x)%k;
        }
        nn/=2;
        x=(x*x)%k;
    }
    return re;
}

void solve()
{
    ll i,j,o;
    ll te;
    cnt[0][0][0]=1;
    ll temp=1;
    ll st;
    ll s;
    for(i=1;i<=n;i++){
        for(j=0;j<k;j++){
            for(o=0;o<=9;o++){
                te=(temp*o+j)%k;
                for(st=0;st<2;st++){
                    s=st;
                    if(i==n && o==0) continue;
                    if(te==0 && o!=0){
                        s=1;
                    }
                    cnt[i][te][s]=(cnt[i][te][s]+cnt[i-1][j][st])%m;
                }
            }
        }
        temp=(temp*10)%k;
    }
}

void out()
{
    ll ans=0;
    ll i;
    for(i=0;i<k;i++){
        ans=(ans+cnt[n][i][1])%m;
    }
    printf("%I64d
",ans);
}

int main()
{
    //freopen("data.in","r",stdin);
   // freopen("data.out","w",stdout);
    //scanf("%d",&T);
    //for(int ccnt=1;ccnt<=T;ccnt++)
    //while(T--)
    while(scanf("%I64d%I64d%I64d",&n,&k,&m)!=EOF)
    {
        ini();
        solve();
        out();
    }
    return 0;
}