1 B样条曲线
1.1 B样条曲线方程
B样条方法具有表示与设计自由型曲线曲面的强大功能,是形状数学描述的主流方法之一,另外B样条方法是目前工业产品几何定义国际标准——有理B样条方法 (NURBS)的基础。B样条方法兼备了Bezier方法的一切优点,包括几何不变性,仿射不变性等等,同时克服了Bezier方法中由于整体表示带来不具有局部性质的缺点(移动一个控制顶点将会影响整个曲线)。B样条曲线方程可表示为
其中,di(i=0,1...n)为控制顶点(坐标),Ni,k(i=0,1...n)为k次规范B样条基函数,最高次数是k。基函数是由一个称为节点矢量的非递减参数u的序列U:u0≤u1≤...≤un+k+1所决定的k次分段多项式。
B样条的基函数通常采用Cox-deBoor递推公式:
![clip_image004[14] clip_image004[14]](https://images2015.cnblogs.com/blog/682014/201605/682014-20160501233215175-351162171.gif) (2)
(2)
式中i为节点序号,k是基函数的次数,共有n+1个控制顶点。注意区分节点和控制顶点,节点是在节点矢量U中取得,控制顶点则是坐标点,决定B样条的控制多边形。Cox-deBoor递推公式是B样条曲线的定义的核心,该公式在程序中的实现可采用递归的方式:

1 function Nik_u = BaseFunction(i, k , u, NodeVector) 2 % 计算基函数Ni,k(u),NodeVector为节点向量 3 4 if k == 0 % 0次B样条 5 if (u >= NodeVector(i+1)) && (u < NodeVector(i+2)) 6 Nik_u = 1.0; 7 else 8 Nik_u = 0.0; 9 end 10 else 11 Length1 = NodeVector(i+k+1) - NodeVector(i+1); 12 Length2 = NodeVector(i+k+2) - NodeVector(i+2); % 支撑区间的长度 13 if Length1 == 0.0 % 规定0/0 = 0 14 Length1 = 1.0; 15 end 16 if Length2 == 0.0 17 Length2 = 1.0; 18 end 19 Nik_u = (u - NodeVector(i+1)) / Length1 * BaseFunction(i, k-1, u, NodeVector) ... 20 + (NodeVector(i+k+2) - u) / Length2 * BaseFunction(i+1, k-1, u, NodeVector); 21 end
所给程序可用于计算基函数Ni,k(u)的值,程序中对不同类型的B样条曲线区别在于节点矢量 NodeVector 的取值不同。
1.2 B样条曲线的分类
根据节点矢量中节点的分布情况不同,可以划分4中类型的B样条曲线。不同类型的B样条曲线区别主要在于节点矢量,对于具有n+1个控制顶点![]() 的 k 次B样条曲线,无论是哪种类型都具有n+k+2个节点
的 k 次B样条曲线,无论是哪种类型都具有n+k+2个节点![]() 。
。
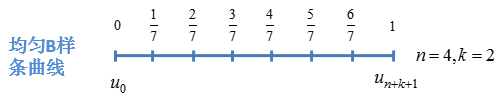
均匀B样条曲线
节点矢量中节点为沿参数轴均匀或等距分布。
准均匀B样条曲线
其节点矢量中两端节点具有重复度k+1,即u0=u1=...=uk,un+1=un+2=...=un+k+1,所有的内节点均匀分布,具有重复度1。
分段Bezier曲线
其节点矢量中两端节点的重复度与类型2相同,为k+1。不同的是内节点重复度为k。该类型有限制条件,控制顶点数减1必须等于次数的正整数倍,即必须满足![]() 正整数。
正整数。
一般非均匀B样条曲线
这里给出准均匀B样条和分段Bezier曲线的生成节点矢量的代码,均匀B样条的很简单就不列出了。假设共n+1个控制顶点,k次B样条,输入参数为 n, k ,输出节点矢量到NodeVector中。

1 function NodeVector = U_quasi_uniform(n, k) 2 % 准均匀B样条的节点向量计算,共n+1个控制顶点,k次B样条 3 NodeVector = zeros(1, n+k+2); 4 piecewise = n - k + 1; % 曲线的段数 5 if piecewise == 1 % 只有一段曲线时,n = k 6 for i = n+2 : n+k+2 7 NodeVector(1, i) = 1; 8 end 9 else 10 flag = 1; % 不止一段曲线时 11 while flag ~= piecewise 12 NodeVector(1, k+1+flag) = NodeVector(1, k + flag) + 1/piecewise; 13 flag = flag + 1; 14 end 15 NodeVector(1, n+2 : n+k+2) = 1; 16 end

1 function NodeVector = U_piecewise_Bezier(n, k) 2 % 分段Bezier曲线的节点向量计算,共n+1个控制顶点,k次B样条 3 % 分段Bezier端节点重复度为k+1,内间节点重复度为k,且满足n/k为正整数 4 5 if ~mod(n, k) && (~mod(k, 1) && k>=1) % 满足n是k的整数倍且k为正整数 6 NodeVector = zeros(1, n+k+2); % 节点矢量长度为n+k+2 7 NodeVector(1, n+2 : n+k+2) = ones(1, k+1); % 右端节点置1 8 9 piecewise = n / k; % 设定内节点的值 10 Flg = 0; 11 if piecewise > 1 12 for i = 2 : piecewise 13 for j = 1 : k 14 NodeVector(1, k+1 + Flg*k+j) = (i-1)/piecewise; 15 end 16 Flg = Flg + 1; 17 end 18 end 19 20 else 21 fprintf('error!\n'); 22 end
1.3 B样条曲线的计算
根据B样条曲线的定义公式(1),曲线上任一点坐标值是参数变量u的函数,用矩阵形式表示
可以看出只要已知控制顶点坐标![]() 、曲线的次数
、曲线的次数![]() 以及基函数
以及基函数![]() ,就完全确定了B样条曲线,其中基函数
,就完全确定了B样条曲线,其中基函数![]() 由Cox-deBoor 公式(2)递推计算。
由Cox-deBoor 公式(2)递推计算。
2 B样条曲面
2.1 B样条曲面方程
![]() ,B样条基
,B样条基![]() 与
与![]() 分别由节点矢量
分别由节点矢量![]() 和
和![]() 按Cox-deBoor递推公式(2)计算。
按Cox-deBoor递推公式(2)计算。
B样条曲面按照沿参数方向u, v所取的节点矢量不同,也可以划分成不同的类型:均匀、准均匀、分片Bezier和非均匀B样条曲面。
2.2 B样条曲面的计算
给定曲面的控制顶点并确定次数后,还需要根据不同类型的B样条曲面沿参数方向的节点矢量才能完全定义一张B样条曲面。要计算B样条曲面上的顶点坐标,首先沿一个参数方向如u向或v向,计算出该方向由控制顶点确定的B样条曲线,如下图中的红色曲线是沿u向生成的二次均匀B样条曲线,一共有四条。
之后将沿u向计算得到的B样条曲线上的点作为新的控制顶点,得到张量网格沿v向计算,得到的曲线就是B样条曲面上的,下图中绿色线段组成的就是沿v向的控制的顶点,蓝颜色的曲线是沿v向的二次均匀B样条曲线构成了一张二次均匀B样条曲面。关于B样条曲面实现的代码在这里可以下载。
参考文献:
[1] 施法中. 计算机辅助几何设计与非均匀有理B样条(修订版)[M]. 北京: 高等教育出版社, 2013.

![clip_image010[4] clip_image010[4]](https://images2015.cnblogs.com/blog/682014/201605/682014-20160501233217441-1151218157.gif)
![clip_image016[4] clip_image016[4]](https://images2015.cnblogs.com/blog/682014/201605/682014-20160501233220019-1661073691.gif)
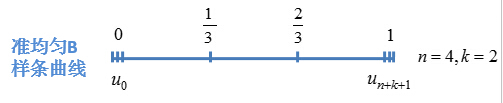
![clip_image022[4] clip_image022[4]](https://images2015.cnblogs.com/blog/682014/201605/682014-20160501233222394-1788300197.gif)
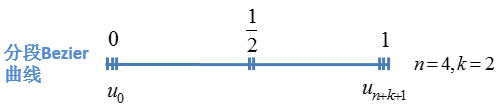
![clip_image030[4] clip_image030[4]](https://images2015.cnblogs.com/blog/682014/201605/682014-20160501233225550-1104832696.gif)
![clip_image034[4] clip_image034[4]](https://images2015.cnblogs.com/blog/682014/201605/682014-20160501233227207-74131496.gif)
![clip_image062[4] clip_image062[4]](https://images2015.cnblogs.com/blog/682014/201605/682014-20160501233239238-345887839.gif)
![clip_image064[4] clip_image064[4]](https://images2015.cnblogs.com/blog/682014/201605/682014-20160501233240785-1388073081.gif)
![clip_image076[4] clip_image076[4]](https://images2015.cnblogs.com/blog/682014/201605/682014-20160501233248332-1716640175.gif)
![clip_image078[4] clip_image078[4]](https://images2015.cnblogs.com/blog/682014/201605/682014-20160501233249253-2000684274.gif)
![clip_image080[4] clip_image080[4]](https://images2015.cnblogs.com/blog/682014/201605/682014-20160501233250378-1417482979.gif)
![clip_image082[4] clip_image082[4]](https://images2015.cnblogs.com/blog/682014/201605/682014-20160501233251425-1317819966.gif)