【文章搬运自我的网易博客(http://zhenxuan1991.blog.163.com/)】
今天下午偶然机会,又去看贝叶斯公式。
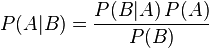
就是这样简单的号称是“概率论中的勾股定理”的一个公式。有非常有趣的一点。
所谓“反直觉”的一点。http://www.guokr.com/article/517/ 这个链接中,果壳网友讨论了一个问题:粗略估计大概每1000人中就有一人得艾滋病。采用某种血液试验检测法用于检测身体中是否含有艾滋病病毒,这种方法相当精确,但也可能带来两种误诊。首先,他可能会让某些真有艾滋病的人得到阴性结果,称为假阴性,不过只有0.05的概率发生;其次,它还可能让某些没有艾滋病的人得到阳性结果,称为假阳性,不过只有0.01的概率会发生。那么如果一个人检测结果为阳性,那么他得艾滋病的概率到底是多大?
当然,解答这个问题,我们要借助贝叶斯公式。
(1)我们定义事件A为“被检测人带有艾滋病病毒”,则A‘表示被检测人不携带艾滋病病毒;定义事件T为“试验结果呈阳性”;
(2)要求概率 P(A|T)。由贝叶斯公式可知:

(3)计算得,P(A|T)=0.087
结论是:如果一个人检测结果为阳性,那么他患病的概率是8.7% 。很低的一个概率。试想,一个人在得知自己的血检是阳性的时候又听说其实患病的概率只是8.7%会有什么感受?
对,唯一的感受是:这哪儿跟哪儿啊?!
可是贝叶斯公式错了吗?推导过程一步步在那摆着呢。那直觉错了吗?直觉怎么会错,难道我看到阳性结果不应该为自己担心吗?
同样在那个链接中,有一个ID为 on9 的人说:我认为这样解释能让更多人容易理解:假设有这么一个理想统计人群,一共有十万人。那么按照文中的发病率千分之一,那么应该有一百人有艾滋病。而根据那两个误诊率,那么这一百个人里面,有九十五个会验出是阳性,而有五个(5%)会被验出为阴性(假阴性)。而在剩下的九万九千九百个没病的人里面,会有九百九十九个人(1%)验出是阳性(假阳性)。因此,总结所有十万个人里面,验出阳性的人有999+95=1094人,其中真正有病的只有95个,占其中的8.68%。那位被验出是阳性的哥,真正杯具的几率只有不到10%!
参考他的说法,我自己又整理了一下思路:用直白的话说,一个健康人检验结果为阳性的概率是0.01,但是有很多“不幸”的健康人落入到这个概率中。而在所有检测为阳性的人中,真正的病人与“不幸”的健康人比例大概为10:90,也就是100个阳性检测结果中,有90个人是健康的。所以就会有这种反直觉的计算结果。而出现这种结果的原因是什么?因为健康人检验结果为阳性的概率(0.01)太高,也就是检测可靠性太低。我算了一下,如果健康人检验结果为阳性的概率降低到0.0001,那么如果一个人检验结果为阳性,那么他患病的概率就飙升到0.9056.
所以我认为,所谓的反直觉这种情况,其实是不存在的。如果机器的检测结果可靠性更好,也不存在“阳性结果患病的概率只有8%”这种情况。而题中所言的0.01的误诊率,其实是非常高的。而这也是我认为唯一存在“反直觉”的地方——在概率与统计中,0.1的误差其实比我们所认为的大得多。