权值线段树模板 + 例题：普通平衡树

权值线段树模板 + 例题：普通平衡树

  权值线段树是线段树的一个扩展，对于某个数，维护他出现的次数，那么对于一段区间维护的就是区间的数出现的次数和，类似一个桶的作用。由于涉及到了统计区间里的所有数出现的次数，那么当数很大的时候，是需要离散化的。以数列：(1， 1， 2， 2， 3， 3， 3， 5) 举例，可以发现值域是：([1, 5])，那么构造的权值线段树如下图：

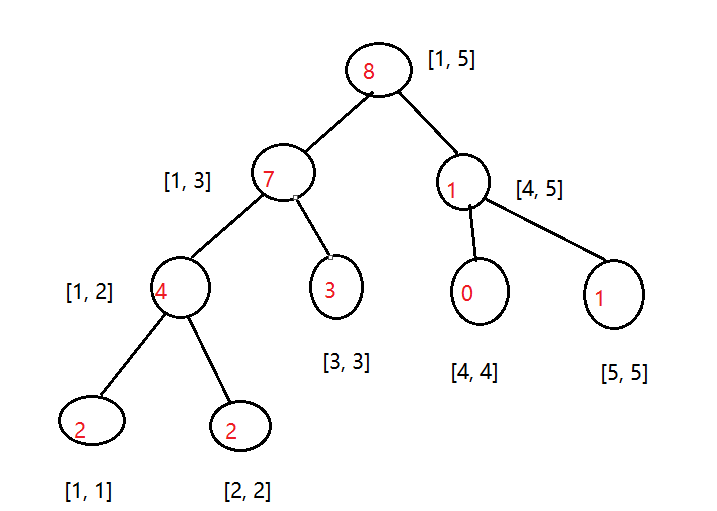
  使用权值线段树我们可以求排名，求第 (k) 大，求前驱和后继。下面是例题：

P3369 【模板】普通平衡树

  基本操作有：

1. 插入 xx 数
2. 删除 xx 数(若有多个相同的数，因只删除一个)
3. 查询 xx 数的排名(排名定义为比当前数小的数的个数 +1+1 )
4. 查询排名为 xx 的数
5. 求 xx 的前驱(前驱定义为小于 xx，且最大的数)
6. 求 xx 的后继(后继定义为大于 xx，且最小的数)

  用权值线段树可以轻松解决，当然平衡树也是可以的。
(Code:)

/*
@Author: nonameless
@Date:   2020-05-30 09:49:17
@Email:  2835391726@qq.com
@Blog:   https://www.cnblogs.com/nonameless/
*/
#include <bits/stdc++.h>
#define x first
#define y second
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) x.begin(), x.end()
using namespace std;
typedef long long ll;
typedef pair<ll, ll> PLL;
typedef pair<int, int> PII;
const double eps = 1e-8;
const double PI  = acos(-1.0);
const int INF = 0x3f3f3f3f;
const ll LNF  = 0x3f3f3f3f3f3f;
inline int gcd(int a, int b) { return b ? gcd(b, a % b) : a; }
inline ll  gcd(ll  a, ll  b) { return b ? gcd(b, a % b) : a; }
inline int lcm(int a, int b) { return a * b / gcd(a, b); }

const int N = 1e5 + 10;

int n;

// 存储操作
struct Num{
    int op, val;
}num[N];

struct Node{
    int l, r; // l, r 代表值域 [l, r]
    int cnt;  // 代表值域 [l, r] 里数的个数
}t[N << 2];

vector<int> vec; // 用来离散化

int findX(int x){ // 计算离散化后的值
    // 如果在之前你没有插入 -1e8, 但你的线段树又是从 1 开始的，那么这里返回值 + 1
    return lower_bound(all(vec), x) - vec.begin();
}

void build(int u, int l, int r){  // 建树
    t[u].l = l, t[u].r = r;
    if(l == r){
        t[u].cnt = 0;
        return;
    }
    int mid = l + r >> 1;
    build(u << 1, l, mid);
    build(u << 1 | 1, mid + 1, r);
    t[u].cnt = t[u << 1].cnt + t[u << 1 | 1].cnt;
}

// 插入和删除，插入时 op = 1, 删除时 op = -1
void update(int u, int x, int op){ 
    if(t[u].l == t[u].r){ // 到叶子结点
        t[u].cnt += op;
        return;
    } else{
        int mid = t[u].l + t[u].r >> 1;
        if(mid >= x) update(u << 1, x, op);
        else update(u << 1 | 1, x, op);
    }
    t[u].cnt = t[u << 1].cnt + t[u << 1 | 1].cnt; // 记得更新
}

// 查询 x 的排名，这里实则是计算区间 [1, x - 1] 里的数的个数
int Rank(int u, int x){ 
    // x > r 代表 x 在区间的右边，返回该区间里数的个数
    if(t[u].r < x) return t[u].cnt;
    int mid = t[u].l + t[u].r >> 1;
    int res = Rank(u << 1, x); // 无论 x 与 mid 的大小，都有计算左边的区间
    if(x > mid + 1) res += Rank(u << 1 | 1, x);
    return res;
}

// 查询排名为 x 的数
int kth(int u, int x){
    if(t[u].l == t[u].r) return t[u].l;
    if(t[u << 1].cnt >= x) return kth(u << 1, x);
    else return kth(u << 1 | 1, x - t[u << 1].cnt);
}

// 查询 u为根 所在树的最大的数
int findRight(int u){
    if(t[u].l == t[u].r) return t[u].l;
    if(t[u << 1 | 1].cnt) return findRight(u << 1 | 1);
    else return findRight(u << 1);
} 

// 查询 x 的前驱
int findPre(int u, int x){
    if(t[u].r < x){
        if(t[u].cnt) return findRight(u);
        return 0;
    }
    int mid = t[u].l + t[u].r >> 1;
    if(x > mid + 1 && t[u << 1 | 1].cnt){
        int res = findPre(u << 1 | 1, x);
        if(res) return res;
    }
    return findPre(u << 1, x);
}

// 查询以 u 为根的树里最小的数
int findLeft(int u){
    if(t[u].l == t[u].r) return t[u].l;
    if(t[u << 1].cnt) return findLeft(u << 1);
    else return findLeft(u << 1 | 1);
}
 

// 查询 x 的后继
int findNxt(int u, int x){
    if(x < t[u].l){
        if(t[u].cnt) return findLeft(u);
        return 0;
    }
    int mid = t[u].l + t[u].r >> 1;
    if(x < mid && t[u << 1].cnt){
        int res = findNxt(u << 1, x);
        if(res) return res;
    }
    return findNxt(u << 1 | 1, x);
}

int main(){

    cin >> n;
    vec.pb(-1e8); // 防止越界，并且方便计算离散化的下标和根据下标映射原值
    for(int i = 1; i <= n; i ++){
        scanf("%d%d", &num[i].op, &num[i].val);
        if(num[i].op != 4) vec.pb(num[i].val); // 操作 4 是排名
    }

    sort(all(vec));
    vec.erase(unique(all(vec)), vec.end());
    int m = sz(vec);

    build(1, 1, m);

    for(int i = 1; i <= n; i ++){

        if(num[i].op == 1) 
            update(1, findX(num[i].val), 1);
        else if(num[i].op == 2) 
            update(1, findX(num[i].val), -1);
        else if(num[i].op == 3)
            printf("%d
", Rank(1, findX(num[i].val)) + 1);
        else if(num[i].op == 4)
            printf("%d
", vec[kth(1, num[i].val)]);
        else if(num[i].op == 5) 
            printf("%d
", vec[findPre(1, findX(num[i].val))]);
        else printf("%d
", vec[findNxt(1, findX(num[i].val))]);
    }

    return 0;
}