1. 背景
深度神经网络（DNNs）在各领域中成功的应用案例，使其成为了迄今为止最受欢迎的机器学习模型之一。但人们担心其易受敌对干扰，因此其在安全相关的环境中的应用受到了限制。
2. 问题描述
网络的复杂性和庞大规模对自动化形式验证技术（automated formal verification technique）构成了挑战。
3. 相关技术
修剪技术：神经元修剪（Neuron Pruning,NP）、权重修剪（Weight Pruning,WP）
验证技术：Marabou、ERAN、MIPVerify。
4. 作者的工作
证明了先进的验证工具通过基于统计技术的预处理能够处理具有实际意义的DNNs。
提出一种新的基于网络修剪（network pruning）的训练管道（training pipeline）。在保持准确性和鲁棒性之间取得平衡，同时使生成的网络（resulting networks）经得起形式化分析（formal analysis）
5. 作者工作细节
5.1 关键思想
只要被修剪后的网络保持可接受的性能，对其进行验证的难度可能比对其未修剪的版本进行验证的难度更小。
5.2 用于验证的修剪：训练管道
5.2.1 网络修剪
减小网络的规模，消除对DNNs性能不重要的部分。以此生成更易于验证的网络。
文章中提出的解决方案基于两种修剪技术：神经元修剪、权重修剪。神经元修剪是指通过提出神经元的方式精简网络，因此会切断经过被移除神经元的所有连接。。其算法如Algorithm 1所示。
第1行：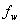
是将被训练的神经网络，稀疏率
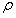指示将被修剪神经元的百分比，
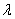为正则化矩阵。
第2行：用损失函数（loss function）和正则化元素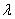
训练网络。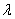
用于使批归一化层（batch normalization layers）的参数
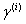无效。SPARSETRAINING中的正则化项可形式化为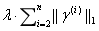
第3、4行：提取批归一化层的权重参数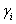
，然后以升序排序。
第5行：将下标等于将要修剪的神经元的数量的权重作为阈值，阈值由权重的数量乘以稀疏率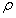
决定。这样，阈值以下的权值的数量正好对应于我们想要修剪的神经元的数量。
第6行：剔除所有与批处理归一化层权值对应的神经元，这些权值都低于第5行计算得出的阈值。
第7行：对修剪后的网络进行再训练，以弥补修剪造成的精度损失（微调，FINETUEN）。
第8行：返回已被修剪的神经网络。
权重修剪指的是，当经过一个神经元的所有连接权重都归零时，剔除该神经元。在该文章中，如果训练后的权值低于用户指定的阈值，则将修剪权值。其算法如Algorithm 2所示。
第2行：用一个标准的训练程序训练神经网络。
第3、4行：从原始网络中提取线性层的权重，并按升序进行排序。
第5行：基于稀疏率参数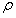
，从有序权重中选择阈值。
第6行：将网络中所有小于阈值的权重设为零，从而得到修剪后的网络。
第7行：微调。
5.2.2 将批归一化层编码为线性层
并不是所有的验证工具都接受具有批归一化层的网络。因此，最终的模型需要没有这些模块，但是训练和神经元修剪需要这些层才能正常工作。
为了克服这一障碍，作者提出了一种后处理技术，将批归一化层和之前的线性层融合成一个新的线性层。
通用线性层和批归一化层的表达式为：
通过将第一个方程中的值代入第二个方程中得到：
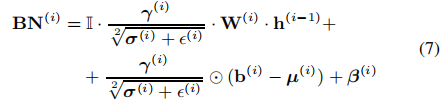
新加入的符号Ⅱ表示维数为维的单位矩阵。因此得到一个融合后的新的线性层的表达式：
6. 数据集、验证工具检查的具体条件
。。。
7. 参数设置、实验结果
。。。
8. 结论
实验组合了修剪算法和验证工具，实验结果表明文章提出的解决方案对于作者考虑的那种网络是成功的，对于修剪和验证技术的组合也是成功的。
使深度神经网络更接近于形式上站得住脚的（formally-grounded）方法。