概括:RNN 适用于处理序列数据用于预测,但却受到短时记忆的制约。LSTM 和 GRU 采用门结构来克服短时记忆的影响。门结构可以调节流经序列链的信息流。LSTM 和 GRU 被广泛地应用到语音识别、语音合成和自然语言处理等。
1. RNN
RNN 会受到短时记忆的影响。如果一条序列足够长,那它们将很难将信息从较早的时间步传送到后面的时间步。 因此,如果你正在尝试处理一段文本进行预测,RNN 可能从一开始就会遗漏重要信息。在反向传播期间,RNN 会面临梯度消失的问题。 梯度是用于更新神经网络的权重值,消失的梯度问题是当梯度随着时间的推移传播时梯度下降,如果梯度值变得非常小,就不会继续学习。

(1)图中的 U W V三种权重参数是共享的;
(2)S_t = f(U*Xt + W*St-1),此处没有写b,有的地方还需要加一个b,f函数一般为tanh;
(3)Ot = softmax(V*St)
随后就是带入数据,更新权重。但这里有一个问题W与U使用bp更新时会有St-1的输入于是乎就有了BPTT的更新算法
图:RNN 的工作模式, 第一个词被转换成了机器可读的向量,然后 RNN 逐个处理向量序列。
|
(1)逐一处理矢量序列 处理时,RNN 将先前隐藏状态传递给序列的下一步。 而隐藏状态充当了神经网络记忆,它包含相关网络之前所见过的数据的信息. |
 |
|
(2)计算隐藏状态 首先,将输入和先前隐藏状态组合成向量, 该向量包含当前输入和先前输入的信息。 向量经过激活函数 tanh之后,输出的是新的隐藏状态或网络记忆.
|
 |
| 激活函数 Tanh:激活函数 Tanh 用于帮助调节流经网络的值。 tanh 函数将数值始终限制在 -1 和 1 之间. |  |
BPTT算法(Back Propagation Through Time)
BPTT其实就是因为输入变量为时间序列所以需要进行进一步的迭代。核心原理还是bp的链式法则。对w的推导:
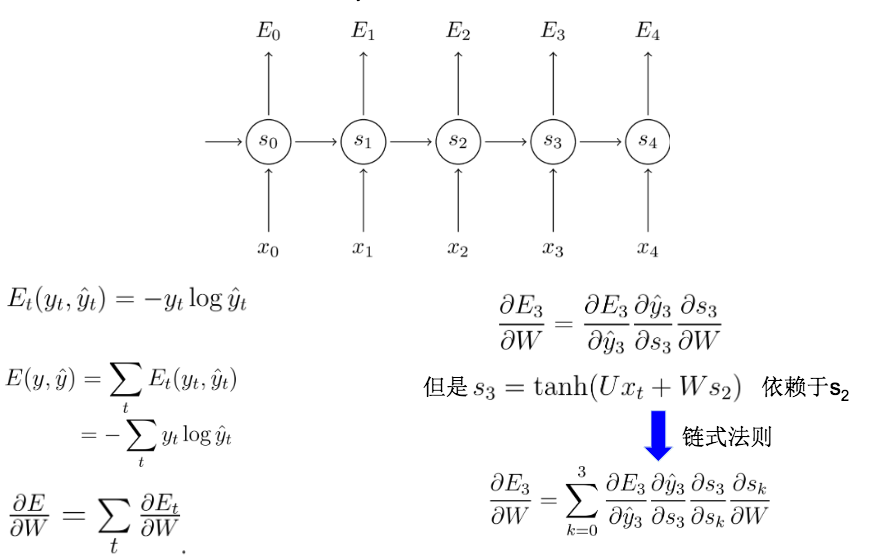
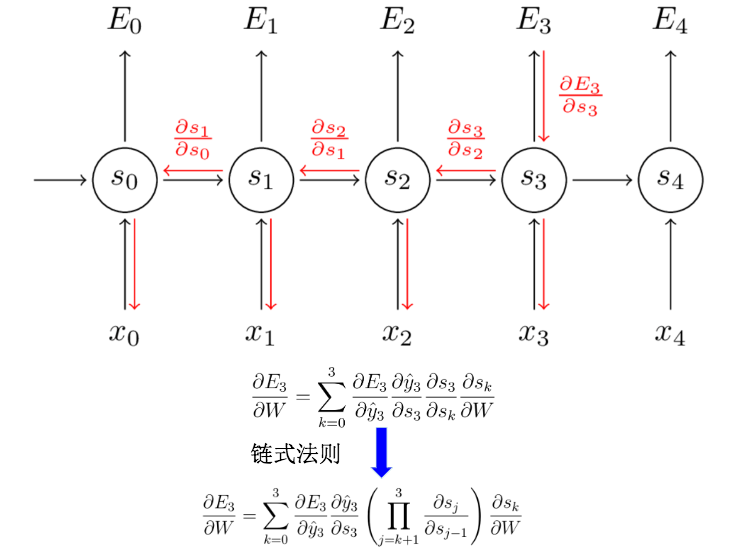
最终就是我们的权重更新公式。
从上面的权重更新公式中,我们会发现里面有非常多的连乘。那么这就会带来一个很大的问题:梯度弥散 / 梯度消失. 这也意味着像DNN一样,随着层次增多,它的训练效率会急剧降低。为了解决梯度消失,于是乎就有LSTM;梯度爆炸 需要用另外的技术来处理,技术上相比梯度消失好解决,因此,很少有人大篇幅去论证这个问题。
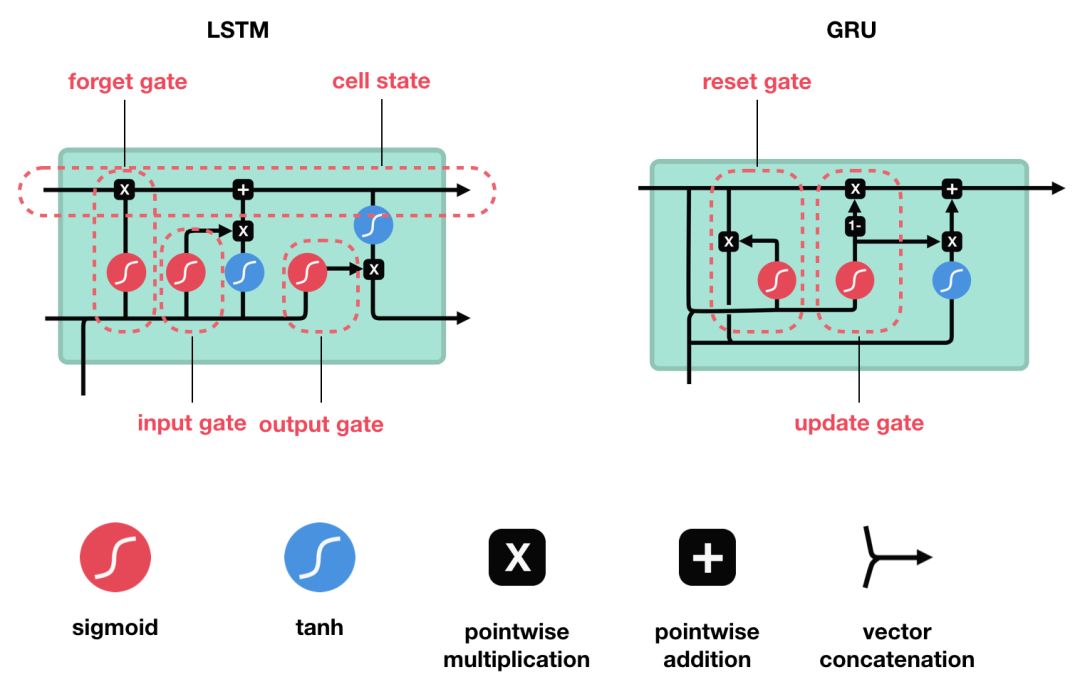
2. LSTM

LSTM 和 GRU 是解决短时记忆问题的解决方案,它们具有称为“门”的内部机制,可以调节信息流。
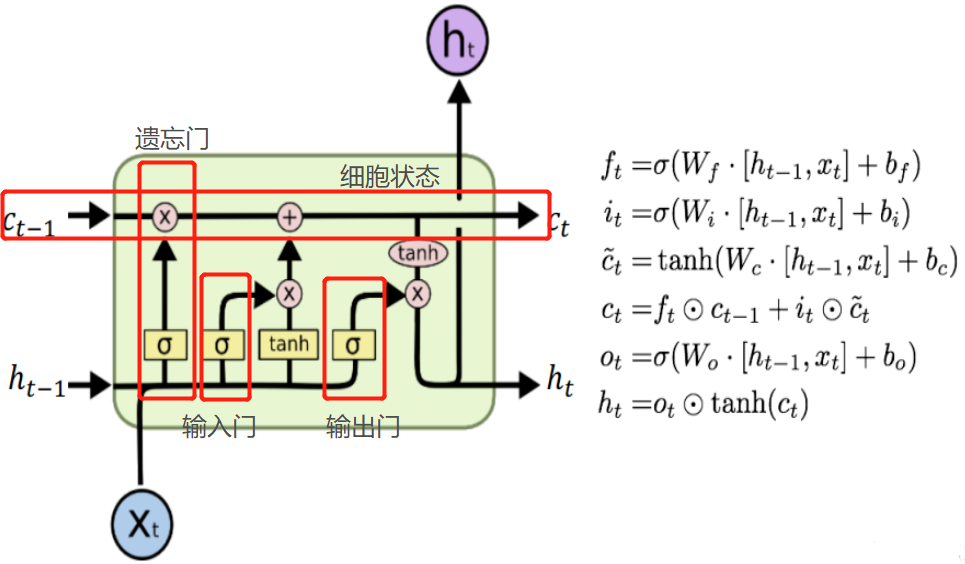
LSTM 的核心概念在于细胞状态以及“门”结构。细胞状态相当于信息传输的路径,让信息能在序列连中传递下去。你可以将其看作网络的“记忆”。理论上讲,细胞状态能够将序列处理过程中的相关信息一直传递下去。其实,LSTM 的记忆能力也没有很高,好像也就 100 来个单词的样子。
|
门的激活函数:Sigmoid 门结构中包含着 sigmoid 激活函数。Sigmoid 激活函数与 tanh 函数类似,不同之处在于 sigmoid 是把值压缩到 0~1 之间而不是 -1~1 之间。这样的设置有助于更新或忘记信息,因为任何数乘以 0 都得 0,这部分信息就会剔除掉。同样的,任何数乘以 1 都得到它本身,这部分信息就会完美地保存下来。这样网络就能了解哪些数据是需要遗忘,哪些数据是需要保存。 |
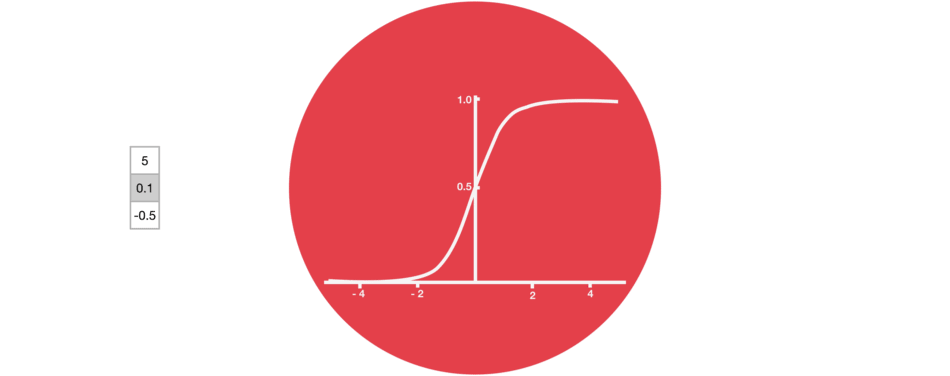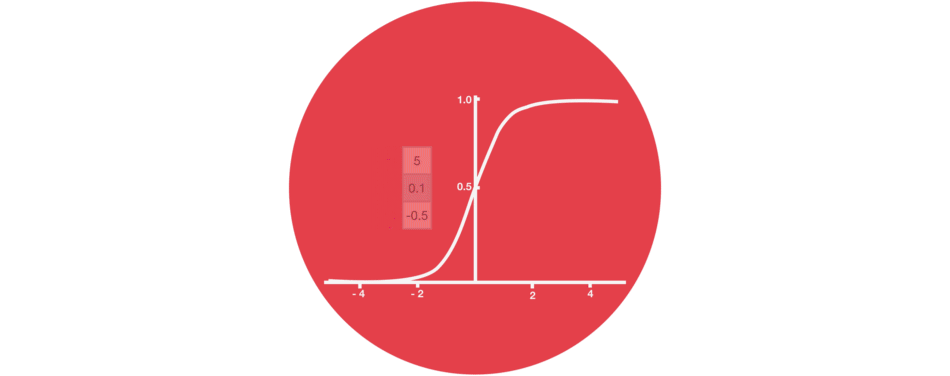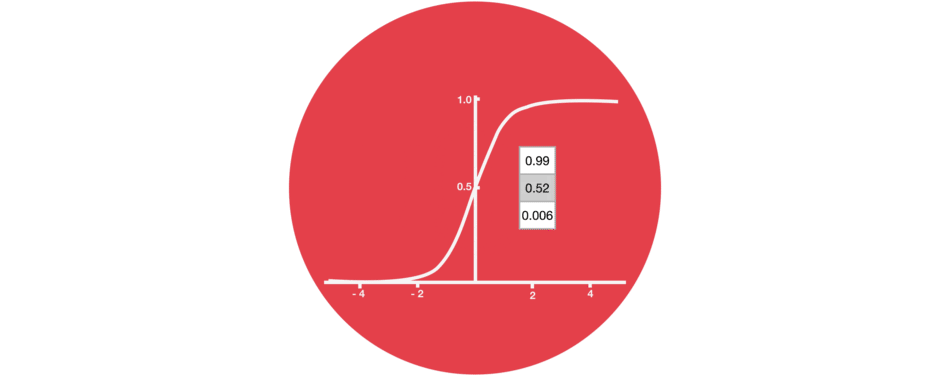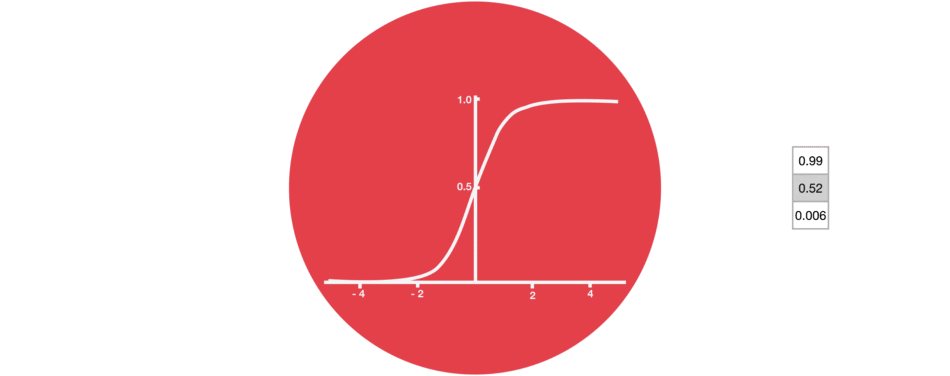 |
|
LSTM 有三种类型的门结构:遗忘门、输入门和输出门 |
 |
|
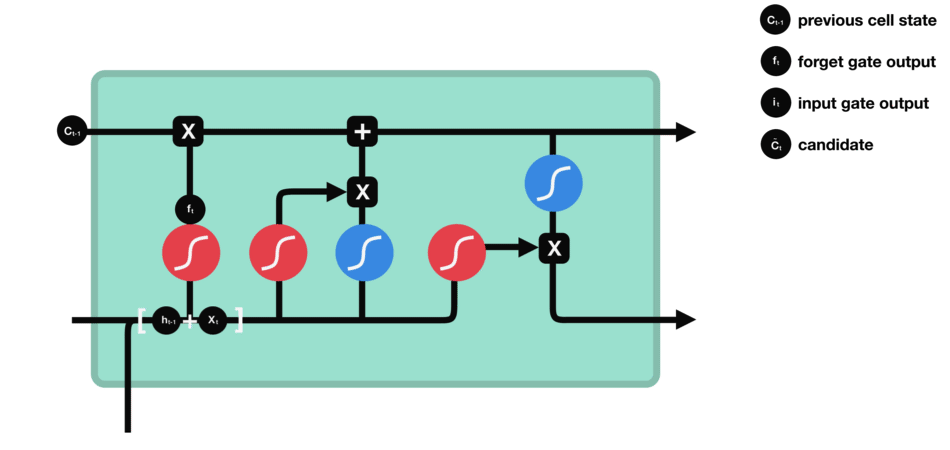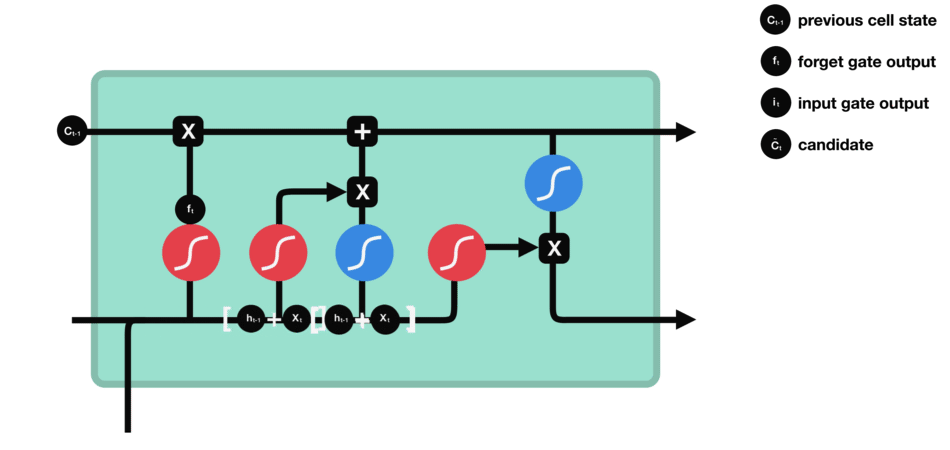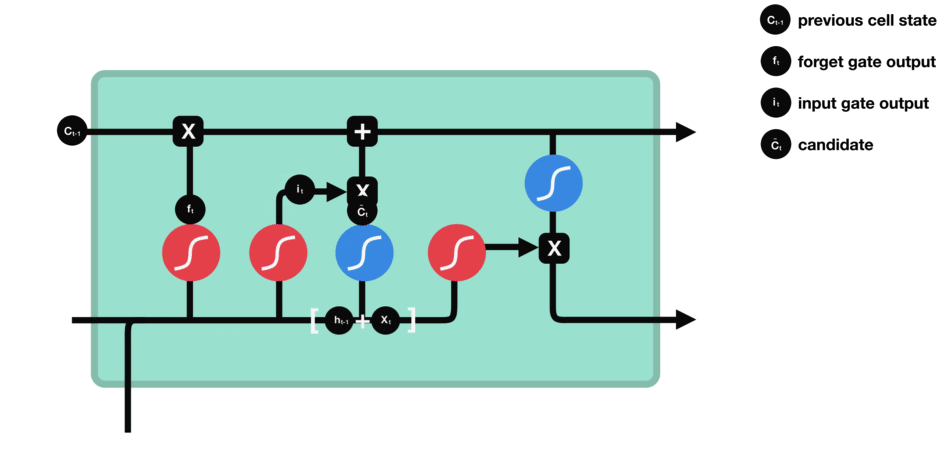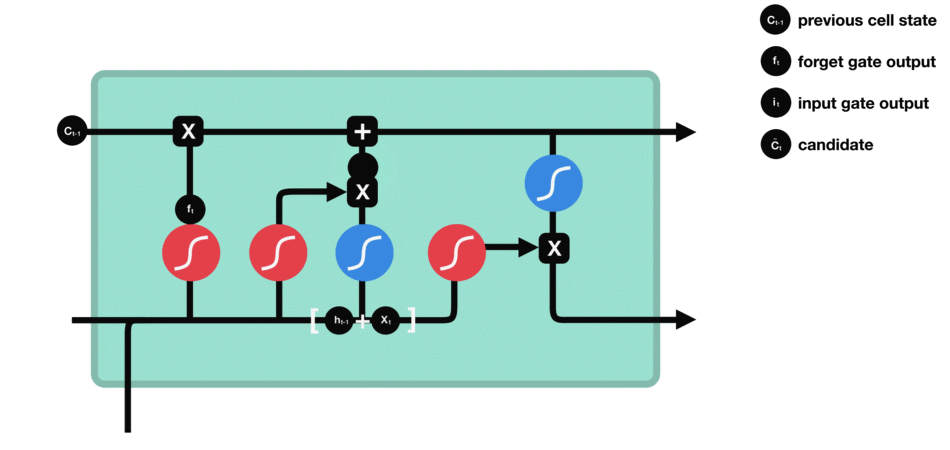
遗忘门 遗忘门的功能是决定应丢弃或保留哪些信息。来自前一个隐藏状态的信息和当前输入的信息同时传递到 sigmoid 函数中去,输出值介于 0 和 1 之间,越接近 0 意味着越应该丢弃,越接近 1 意味着越应该保留。 |
 |
|
输入门 输入门用于更新细胞状态。首先将前一层隐藏状态的信息和当前输入的信息传递到 sigmoid 函数中去。将值调整到 0~1 之间来决定要更新哪些信息。0 表示不重要,1 表示重要。 其次还要将前一层隐藏状态的信息和当前输入的信息传递到 tanh 函数中去,创造一个新的侯选值向量。最后将 sigmoid 的输出值与 tanh 的输出值相乘,sigmoid 的输出值将决定 tanh 的输出值中哪些信息是重要且需要保留下来的。 |
 |
|
细胞状态 下一步,就是计算细胞状态。首先前一层的细胞状态与遗忘向量逐点相乘。如果它乘以接近 0 的值,意味着在新的细胞状态中,这些信息是需要丢弃掉的。然后再将该值与输入门的输出值逐点相加,将神经网络发现的新信息更新到细胞状态中去。至此,就得到了更新后的细胞状态。 |
 |
|
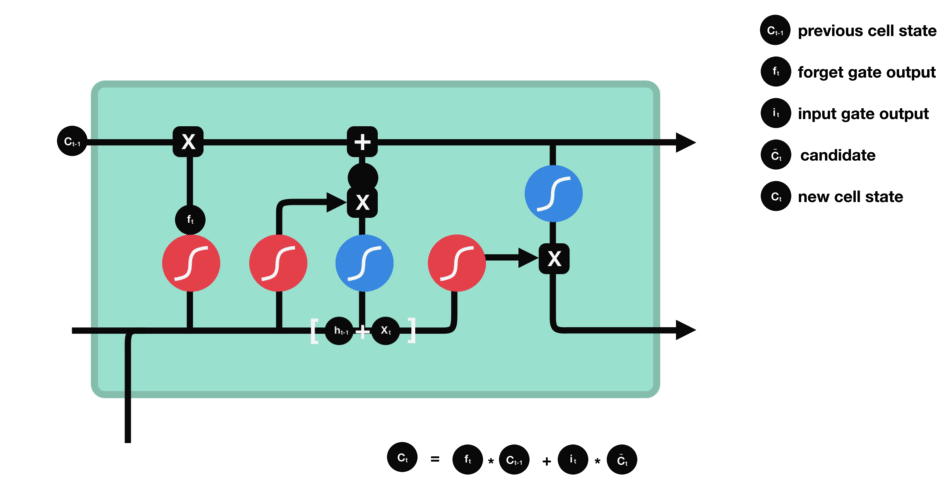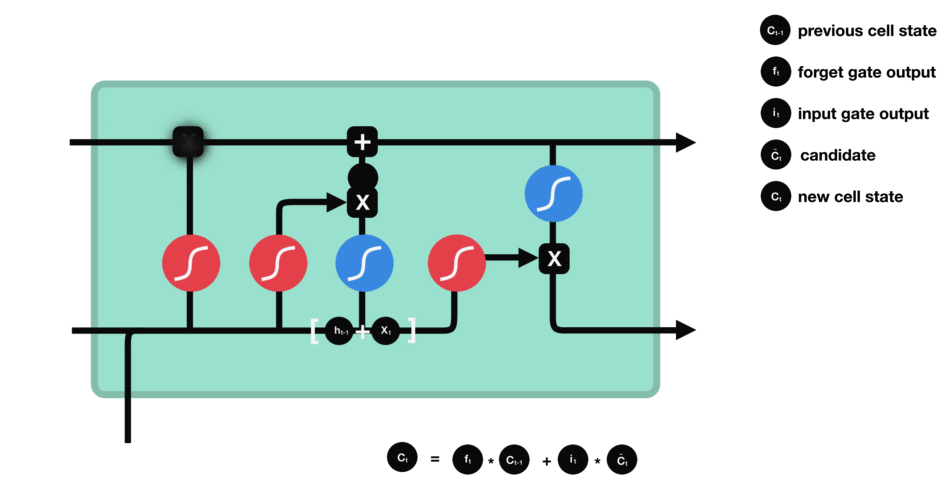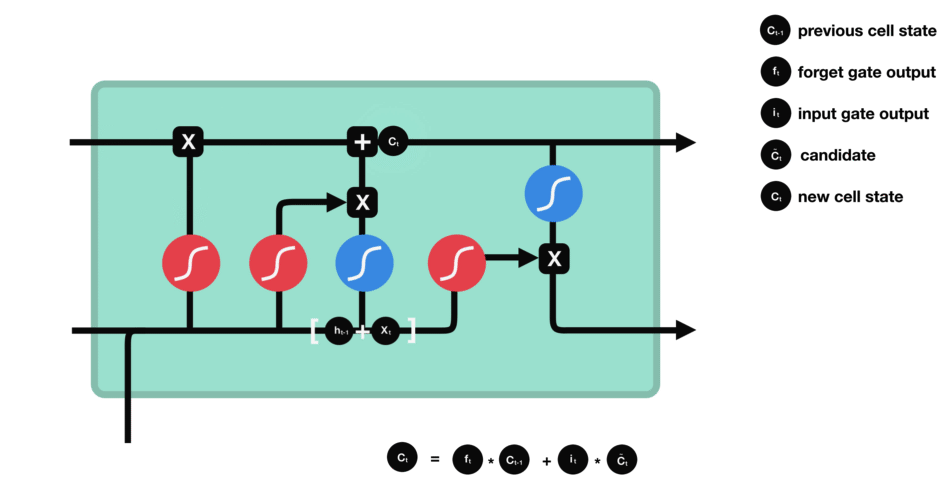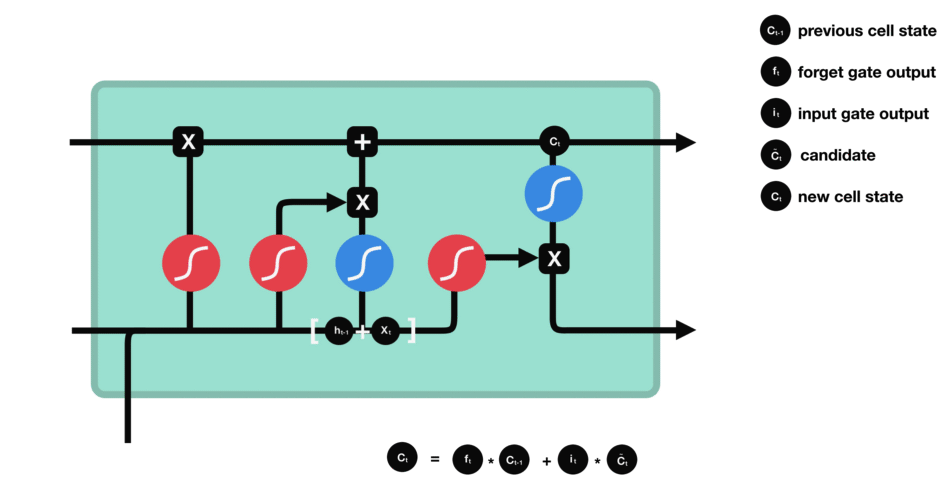
输出门 输出门用来确定下一个隐藏状态的值,隐藏状态包含了先前输入的信息。首先,我们将前一个隐藏状态和当前输入传递到 sigmoid 函数中,然后将新得到的细胞状态传递给 tanh 函数。 最后将 tanh 的输出与 sigmoid 的输出相乘,以确定隐藏状态应携带的信息。再将隐藏状态作为当前细胞的输出,把新的细胞状态和新的隐藏状态传递到下一个时间步长中去。 |
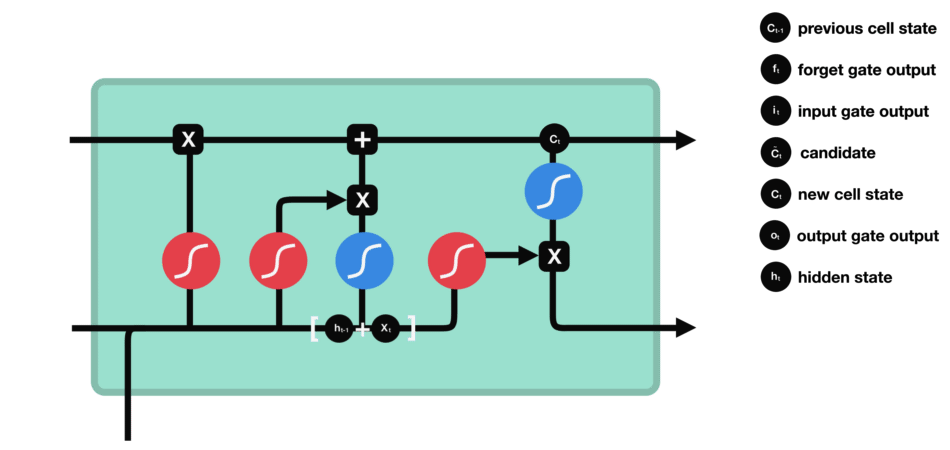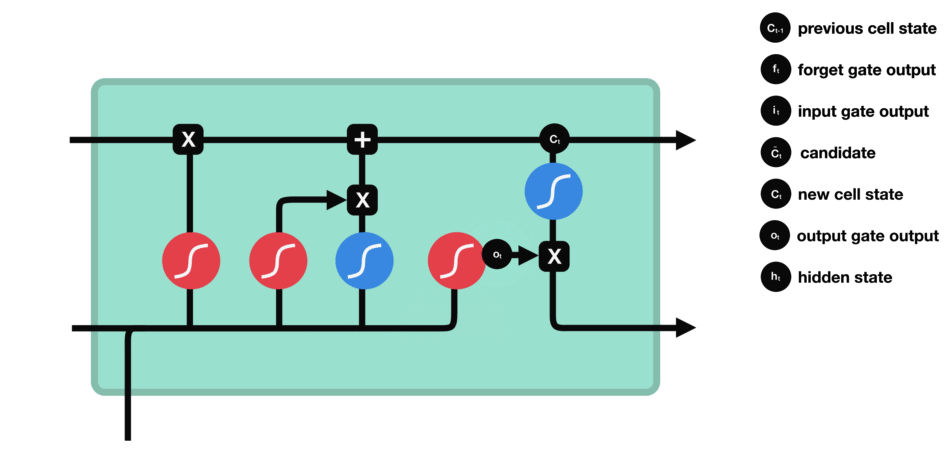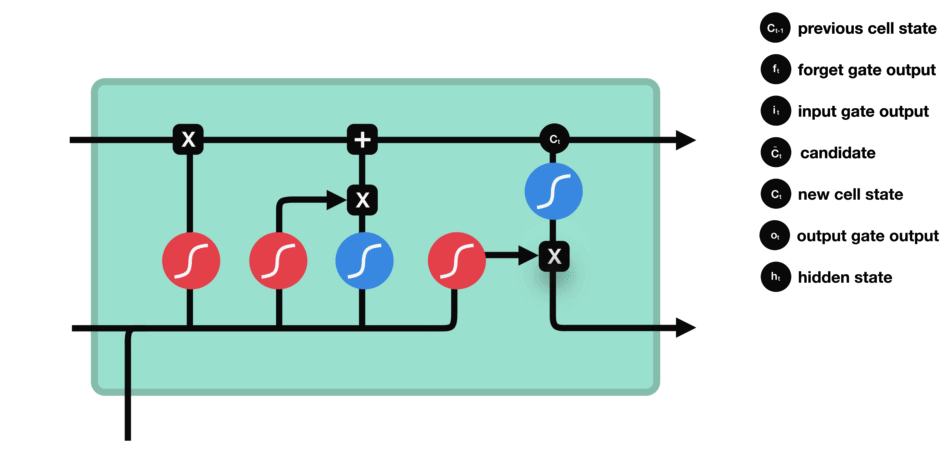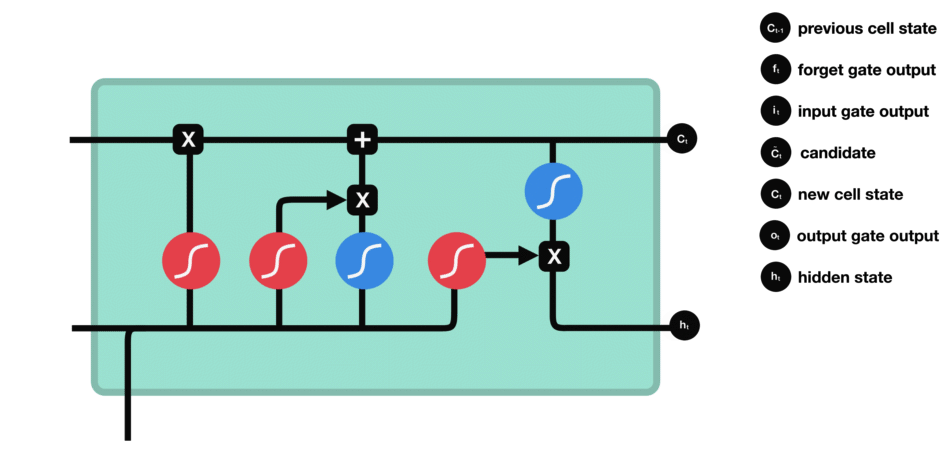 |
具体公式:
下图是Recurrent NN的结构图

如果将每个时间步的网络称为A,并且每个网络换成LSTM的gated cell,则得到以下两个图的LSTM结构。这里的LSTM cell指的是一层cells,即A;而不是MLP中的一个节点。
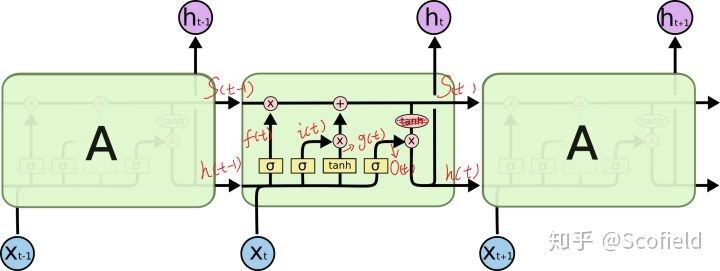

num_units指的是一层的output size(hidden size),可以不与xt的维度相等。因为LSTM cell
还会有一个非线性变换,即Wt的权重矩阵会变换input dim为output size,故权重矩阵使得在timestep t的x的dim变换为output hidden size。
LSTM的参数数量:以seq2seq的encoder-decoder结构的LSTM网络为例


假设:encoder、decoder各只有一层LSTM
cell的units_num(hidden size)=1000
steps=2000
word embedding dim(x_dim)=500
vocab size=50000
(1)Embedding:word embedding dim*vocab size = 50,000*500=25M
(2)Encoder:(hidden size * (hidden size + x_dim) + hidden size) * 4 = (1000 * 1500 + 1000) * 4 = 8M (4组gate)
(hidden size + x_dim )这个即: ,这是LSTM的结构所决定的,注意这里跟time_step无关,
(3)Decoder:同encoder=8M
(4)output:Word embedding dim * Decoder output = Word embedding dim * Decoder hidden size = 50,000 * 1000 = 50M
所以总共有:25M + 8M + 8M + 50M = 91M
总结:
- 权重的计算与time_step无关,LSTM权值共享.
- (hidden size + x_dim )这个亦即:
,这是LSTM的结构所决定的,注意这里跟time_step无关
- 参数权重的数量,占大头的还是vocab size与embedding dim 以及output hidden size.
- LSTM的参数是RNN 的 一层的4倍的数量。
3. GRU
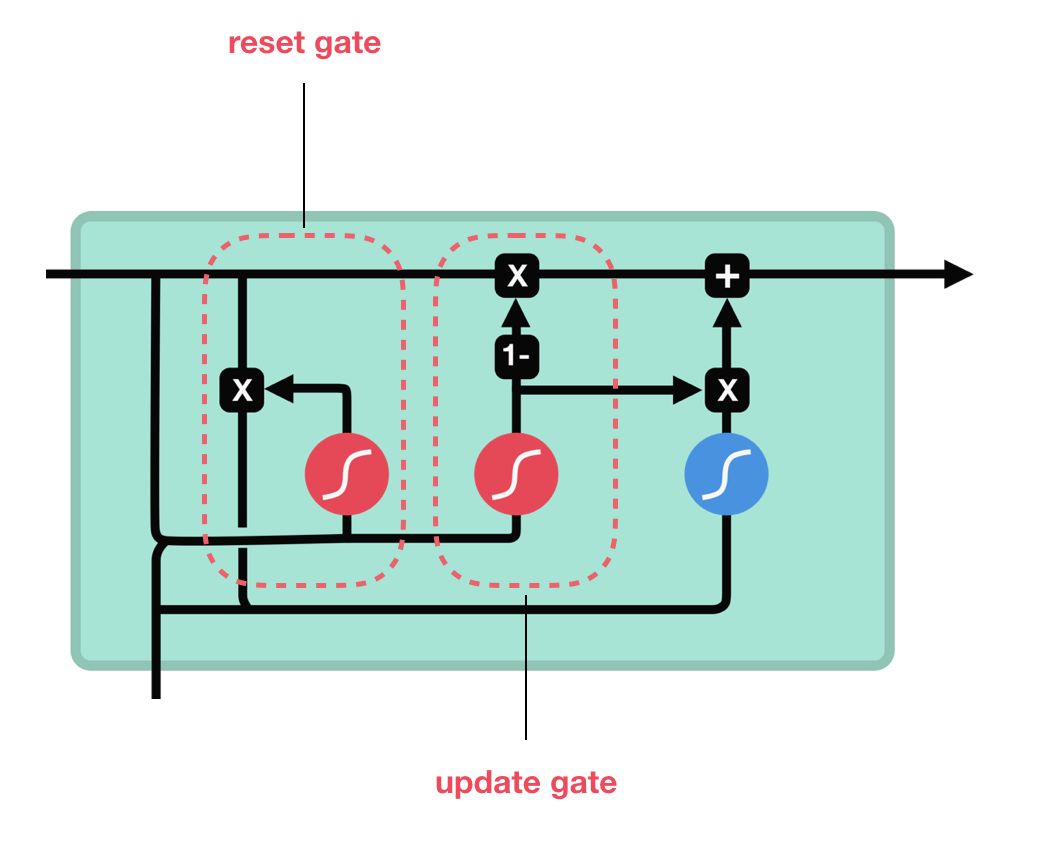
两个门:
(1)更新门
更新门的作用类似于 LSTM 中的遗忘门和输入门。它决定了要忘记哪些信息以及哪些新信息需要被添加。
(2)重置门
重置门用于决定遗忘先前信息的程度。
GRU 的张量运算较少,因此它比 LSTM 的训练更快一下。很难去判定这两者到底谁更好,研究人员通常会两者都试一下,然后选择最合适的。
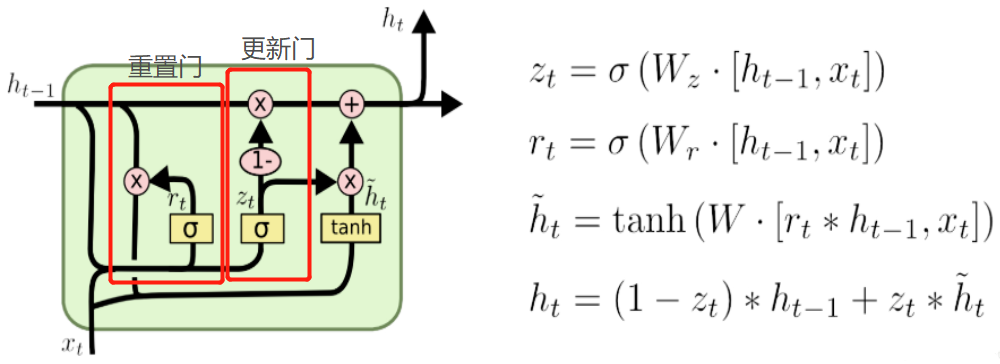
具体公式:
4. seq2seq


参考文献:
【3】LSTM与GRU
【5】LSTM的参数问题?
【6】http://www.huaxiaozhuan.com/%E6%B7%B1%E5%BA%A6%E5%AD%A6%E4%B9%A0/chapters/6_RNN.html