(color{#0066ff}{ 题目描述 })
你有一支由 (n) 名预备役士兵组成的部队,士兵从 (1) 到 (n) 编号,要将他们拆分 成若干特别行动队调入战场。出于默契的考虑,同一支特别行动队中队员的编号 应该连续,即为形如((i, i + 1, ..., i + k))的序列。 编号为 i 的士兵的初始战斗力为 xi ,一支特别行动队的初始战斗力 x 为队内 士兵初始战斗力之和,即 (x = x_i + x_{i+1} + ... + x_{i+k})
通过长期的观察,你总结出一支特别行动队的初始战斗力 (x) 将按如下经验公 式修正为 (x':x'= ax^2+bx+c)其中 (a, b, c) 是已知的系数((a < 0))。 作为部队统帅,现在你要为这支部队进行编队,使得所有特别行动队修正后 战斗力之和最大。试求出这个最大和。
例如,你有 4 名士兵, (x_1 = 2, x_2 = 2, x_3 = 3, x_4 = 4)。经验公式中的参数为 (a = –1, b = 10, c = –20)。此时,最佳方案是将士兵组成 (3) 个特别行动队:第一队包含士兵 (1) 和士兵 (2),第二队包含士兵 (3),第三队包含士兵 (4)。特别行动队的初始战斗力分 别为 (4, 3, 4),修正后的战斗力分别为 (4, 1, 4)。修正后的战斗力和为 (9),没有其它 方案能使修正后的战斗力和更大。
(color{#0066ff}{输入格式})
输入由三行组成。第一行包含一个整数 (n),表示士兵的总数。第二行包含三 个整数 (a, b, c),经验公式中各项的系数。第三行包含 (n) 个用空格分隔的整数 (x_1, x_2, …, x_n),分别表示编号为 (1, 2, …, n) 的士兵的初始战斗力。
(color{#0066ff}{输出格式})
输出一个整数,表示所有特别行动队修正后战斗力之和的最大值。
(color{#0066ff}{输入样例})
4
-1 10 -20
2 2 3 4
(color{#0066ff}{输出样例})
9
(color{#0066ff}{数据范围与提示})
20%的数据中,n ≤ 1000;
50%的数据中,n ≤ 10,000;
100%的数据中,1 ≤ n ≤ 1,000,000,–5 ≤ a ≤ –1,|b| ≤ 10,000,000,|c| ≤ 10,000,000,1 ≤ xi ≤ 100
(color{#0066ff}{题解})
不难得出DP式子
(f[i])代表(1 o i)分组的答案, (s[i])代表每个人x的前缀和
则(f[i] = f[j-1] + a*(s[i]-s[j-1])^2+b*(s[i]-s[j-1])+c)
(f[i]=f[j-1]+a*s[i]^2+a*s[j-1]^2-2*a*s[i]*s[j-1]+b*s[i]-b*s[j-1]+c)
(f[i]=f[j-1]+a*s[j-1]^2-2*a*s[i]*s[j-1]-b*s[j-1]+a*s[i]^2+b*s[i]+c)
令(t=a*s[i]^2+b*s[i]+c)
(f[i]=f[j-1]+a*s[j-1]^2-(2*a*s[i]+b)*s[j-1])
令(k(斜率)=(2*a*s[i]+b))
(k*s[j-1]+f[i]=f[j-1]+a*s[j-1]^2+t)
看成平面上的点((s[j-1],f[j-1]+a*s[j-1]^2)),t最后加就行了
f[i]作为直线的截距,我们要找最大截距,即维护上凸包
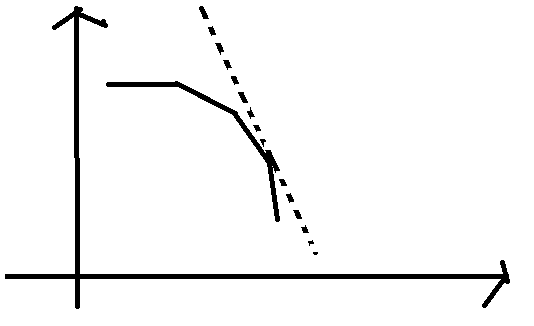
虚线即当前斜率k
则当且仅当k在两个斜率之间的那个交点处最优
取到最优点后,再维护凸包
可以用双端队列
#include<bits/stdc++.h>
#define LL long long
LL in() {
char ch; int x = 0, f = 1;
while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
return x * f;
}
const int maxn = 1e6 + 100;
const LL inf = 999999999999999LL;
LL f[maxn], s[maxn], a, b, c;
int n;
int head, tail, q[maxn];
LL X(int x) { return s[x]; }
LL Y(int x) { return f[x] + a * s[x] * s[x]; }
double k(int x, int y) { return (double)(Y(x) - Y(y)) / (double)(X(x) - X(y)); }
int main() {
n = in(), a = in(), b = in(), c = in();
for(int i = 1; i <= n; i++) s[i] = s[i - 1] + in();
for(int i = 1; i <= n; i++) {
LL K = 2LL * a * s[i] + b;
LL t = a * s[i] * s[i] + b * s[i] + c;
while(head < tail && K < k(q[head + 1], q[head])) head++;
f[i] = Y(q[head]) + t - K * X(q[head]);
while(head < tail && k(q[tail], q[tail - 1]) < k(q[tail], i)) tail--;
q[++tail] = i;
}
printf("%lld
", f[n]);
return 0;
}