【Cesium 历史博客】地平线剔除算法

Horizon Culling | cesium.com

在开发 Cesium 程序时，需要快速确定场景中的对象什么时候不可见，从而判断它不需要渲染。

一种方法是使用视锥体平视剔除，但是还有另一种重要的剔除方法是地平线剔除。

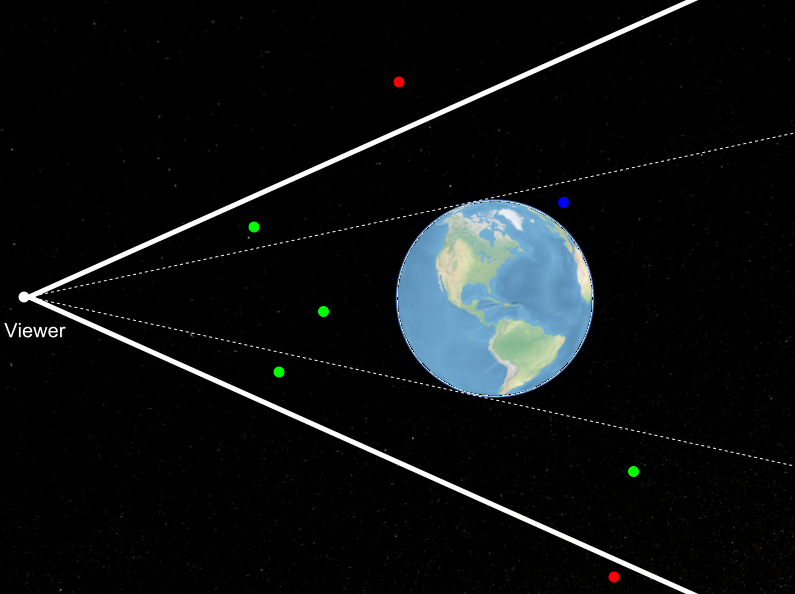
上图中，绿色点是 viewer 内可见的。红色点是不可见的，因为它们在视锥体外面（视锥体用粗白线画出）。蓝色点虽然在视锥体内，但是它在地球背面，所以它也是不可见的。换句话说，它在地平线下。

地平线剔除的思路很简单，即不需要渲染 viewer 视野中地平线之下的东西。听起来简单，但是细节挺多的，尤其是要考虑到性能问题（要快速剔除）。Cesium 每次渲染时，为了检测这些地形瓦片的可见性，就要测试上百次，不过这很重要。

相对于球体的地平线下点剔除

可为所有静态对象（例如瓦片）计算其范围球体（boundingSphere）。假设这个范围球体很小以至于与地球比起来，像一个点，如果这个点在地平线下，那么我们也能说这个瓦片就在地平线下。

当前提出的新算法仅限于对椭球体计算单个点的情况。现在不妨设“遮挡点”已经被计算出来了。

为了说明简便，先进行正球体的地平线剔除，然后再推广到椭球体的地平线剔除。

考虑下面这张图片：

上图中，蓝色的圆是一个单位球面，从 Viewer 向外延申并和单位球面相切的这两条细黑线表示地平线。

垂直的这根粗黑线表示地平线交单位球面的所有地平点，是一个圆。

从 Viewer 到这个圆上的所有点的向量，就构成了一个圆锥体（包括阴影部分）。

译者注

想象一下一个漏斗套一个乒乓球，大概就是这个情况

图中阴影部分表示地平线以下的区域，Viewer 看不到这些区域。换句话说，如果一个点在这个阴影区域，那么这个点就在地平线下。

计算某点位于平面的哪一侧

首先，做一个简单的计算，来算出这个点在垂直黑直线那个圆的圆面的哪一边：

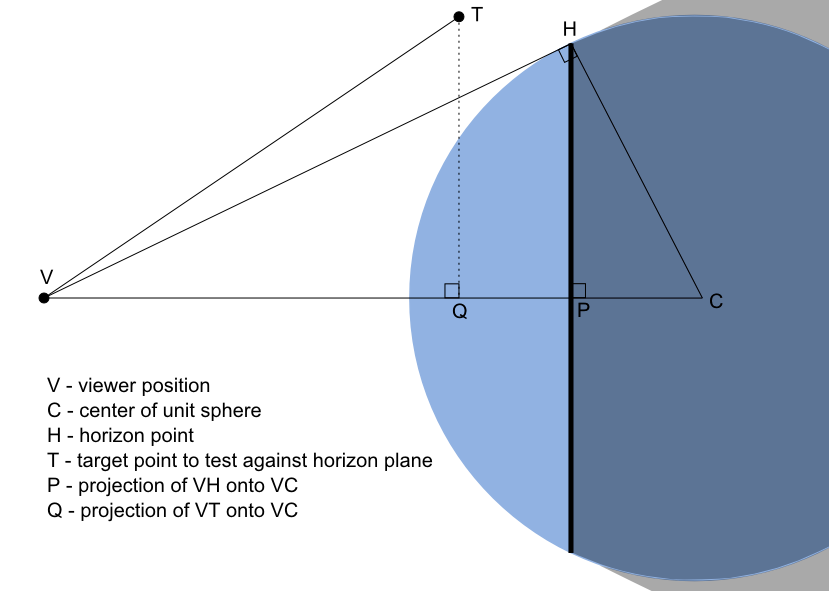
• V：Viewer的位置
• C：单位球面的中心
• H：地平线切单位球面的点
• T：待计算的目标点
• P：H点投影到VC向量的点
• Q：T点投影到VC向量的点

由勾股定理：

[||vec{VH}||^2 + ||vec{HC}||^2 = ||vec{VC}||^2 ]

由单位球，易得 (vec{HC}) 向量的长度是1：

[||vec{VH}||^2 = ||vec{VC}||^2-1 ]

易证 (△VCH) 和 (△HCP) 相似，所以有：

[frac{||vec{PC}||}{||vec{HC}||}=frac{||vec{HC}||}{||vec{VC}||} ]

代入 (||vec{HC}|| =1)，整理得

[||vec{PC}||=frac{1}{||vec{VC}||} ]

所以，Viewer 到平面（下文均用平面简称，即地平线与球面相切的所有点的集合构成的圆周代表的面，即图上垂直黑色粗线）的距离：

[||vec{VP}||=||vec{VC}|| - frac{1}{||vec{VC}||} ]

如果，(vec{VT}) 在 (vec{VC}) 的投影 (vec{VQ}) 长度小于 (vec{VP})，那么点就在平面内（视锥内）。

换句话说，如果 (||vec{VQ}||>||vec{VP}||)，那么点就在地平线下：

[||vec{VQ}||=||vec{VT}||cos(vec{VT}, vec{VC})=vec{VT}·hat{VC}>||vec{VP}||=||vec{VC}|| - frac{1}{||vec{VC}||} ]

左右均乘以 (||vec{VC}||)，即

[vec{VT}·hat{VC}·||vec{VC}||=vec{VT}·vec{VC}>||vec{VC}||^2-1 ]

结论

若想知道目标点位于平面的前面还是后面，只需取 Viewer 到目标点的向量 (vec{VT})、Viewer 到单位球心的向量 (vec{VC})，求其内积，判断结果与 Viewer 到单位球心距离与1的差的大小即可。

若大于，则点在地平线下（平面后），反之则在平面前（地平线上）

判断目标点与圆锥体的关系

仍旧是考虑原来的图，这次考虑两个角 (∠HVC)（记为α）、(∠TVC)（记为β）

当角 β < α 时，目标点 T 就位于圆锥内了。

在 ([0, π]) 区间上，对于任意的 β > α，有

[cos(β) > cos(α) ]

角 α 是 (Rt△VCH) 的一个角，所以：

[cos(β) > frac{||vec{VH}||}{||vec{VC}||} ]

由余弦的定义，cos(β) 可写为

[cos(β) = frac{vec{VT}·vec{VC}}{||vec{VT}||·||vec{VC}||} ]

即

[cos(β) = frac{vec{VT}·vec{VC}}{||vec{VT}||·||vec{VC}||} > frac{||vec{VH}||}{||vec{VC}||} ]

两边同时乘上 (||vec{VC}||) 并同时平方，则

[frac{(vec{VT}·vec{VC})^2}{||vec{VT}||^2}>||vec{VH}||^2 ]

根据上一节的计算结果 (||vec{VH}||^2=||vec{VC}||^2-1)

最终，得到的不等式关系是：

[frac{(vec{VT}·vec{VC})^2}{||vec{VT}||^2}>||vec{VC}||^2-1 ]

(vec{VT}) 和 (vec{VC}) 都很容易计算，若上式不等号成立，则说明目标点在视锥内，否则在视锥外。

推广到椭球体的情况

上述均为单位球的情况，现在推广到椭球体上。

单位球的方程是：

[x^2+y^2+z^2=1 ]

椭球体的方程是：

[frac{x^2}{a^2}+frac{y^2}{b^2}+frac{z^2}{c^2}=1 ]

其中，a、b、c是三个轴的半长（轴半径）。

利用缩放矩阵，可以将椭球体上的所有点归为单位球上的计算：

[M=egin{bmatrix} displaystylefrac{1}{a} & 0 & 0 \ 0 & displaystylefrac{1}{b} & 0 \ 0 & 0 & displaystylefrac{1}{c} \ end{bmatrix} ]

代码

作者认为数学推导过程很重要，但是可以归结成一些简单的代码。每当摄像机位置改变时，都要执行

// 椭球的三个轴半径 此处使用 WGS84椭球体
var rX = 6378137.0;
var rY = 6378137.0;
var rZ = 6356752.3142451793;

// 向量CV，缩放到单位球空间（除以各轴半径），方便计算
var cvX = cameraPosition.x / rX;
var cvY = cameraPosition.y / rY;
var cvZ = cameraPosition.z / rZ;
// 向量VH长度的平方
var vhMagnitudeSquared = cvX * cvX + cvY * cvY + cvZ * cvZ - 1.0;

然后对于每个点，要进行测试遮挡剔除算法：

// 目标点T，缩放到单位球空间（除以各轴半径），方便计算
var tX = position.x / rX;
var tY = position.y / rY;
var tZ = position.z / rZ;

// 向量VT
var vtX = tX - cvX;
var vtY = tY - cvY;
var vtZ = tZ - cvZ;
// 向量VT长度的平方
var vtMagnitudeSquared = vtX * vtX + vtY * vtY + vtZ * vtZ;

// VT点乘VC 和 VT点乘CV的相反数是一样的
var vtDotVc = -(vtX * cvX + vtY * cvY + vtZ * cvZ);

// bool值，前者是判断是否在平面内，后者判断是否在锥体内
var isOccluded = vtDotVc > vhMagnitudeSquared && vtDotVc * vtDotVc / vtMagnitudeSquared > vhMagnitudeSquared;

在 Cesium 中，预先进行了单位球空间的缩放，而不是每次测试都缩放。

EllipsoidalOccluder.prototype.isPointVisible = function (occludee) {
  var ellipsoid = this._ellipsoid;
  var occludeeScaledSpacePosition = ellipsoid.transformPositionToScaledSpace(
    occludee,
    scratchCartesian
  );
  return isScaledSpacePointVisible(
    occludeeScaledSpacePosition,
    this._cameraPositionInScaledSpace,
    this._distanceToLimbInScaledSpaceSquared
  );
};

展望

与之前使用最小范围球进行剔除的方法相比，使用这个技术减少大约 15% 的瓦片绘制。

其他就不翻译了

实际应用

在 Cesium 的私有类 EllipsoidalOccluder （位于Core目录下）中，就使用了这个算法进行剔除计算。