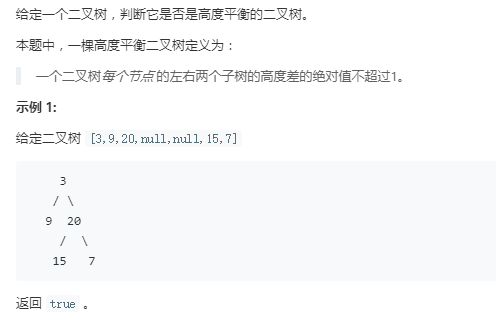

求二叉树是否平衡,根据题目中的定义,高度平衡二叉树是每一个结点的两个子树的深度差不能超过1,那么我们肯定需要一个求各个点深度的函数,然后对每个节点的两个子树来比较深度差,时间复杂度为O(NlgN),代码如下:
1 /** 2 * Definition for a binary tree node. 3 * struct TreeNode { 4 * int val; 5 * TreeNode *left; 6 * TreeNode *right; 7 * TreeNode(int x) : val(x), left(NULL), right(NULL) {} 8 * }; 9 */ 10 class Solution { 11 public: 12 //求左右子树深度差,那我们需要一个求左右子树深度的函数,然后比较就可以了 13 bool isBalanced(TreeNode* root) { 14 if(!root) return true;//空树也是平衡二叉树,单节点也是平衡二叉树 15 if(abs(getdepth(root->left)-getdepth(root->right)) > 1) return false; 16 return isBalanced(root->left) && isBalanced(root->right); 17 } 18 //得到每个节点为root时候的深度,平衡二叉树要求每个节点都复合这样的。 19 int getdepth(TreeNode *root){ 20 if(!root) return 0; 21 return 1+max(getdepth(root->left),getdepth(root->right)); 22 } 23 };
上面的方法每个点计算深度的时候都会被访问一次,我们可以进行优化。方法是如果我们发现子树不平衡,则不计算具体的深度,而是直接返回-1。那么优化后的方法为:对于每一个节点,我们通过checkDepth方法递归获得左右子树的深度,如果子树是平衡的,则返回真实的深度,若不平衡,直接返回-1,此方法时间复杂度O(N),空间复杂度O(H),参见代码如下:
1 class Solution { 2 public: 3 bool isBalanced(TreeNode *root) { 4 if (checkDepth(root) == -1) return false; 5 else return true; 6 } 7 int checkDepth(TreeNode *root) { 8 if (!root) return 0; 9 int left = checkDepth(root->left); 10 if (left == -1) return -1; 11 int right = checkDepth(root->right); 12 if (right == -1) return -1; 13 int diff = abs(left - right); 14 if (diff > 1) return -1; 15 else return 1 + max(left, right); 16 } 17 };