AT2668 [AGC017E] Jigsaw 题解

Link.

ATcoder
Luogu

Description.

（这个是题目大意）
有很多块积木，形如下图

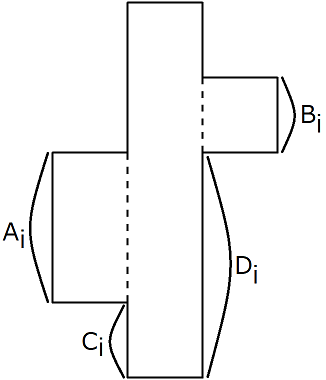
问能否构造一种方式，使得满足

1. 每个积木都被用上
2. 没有一块积木悬空
3. 积木要么在地上要么放在另一块积木上
4. 积木正中间必须在地上

Solution.

我只能膜拜 @\(\text{F}\color{red}{\text{lying2018}}\)

首先建点连边，每条边表示一个积木。
然后把积木拆开，拆成左半边和右半边，然后分成两类点。

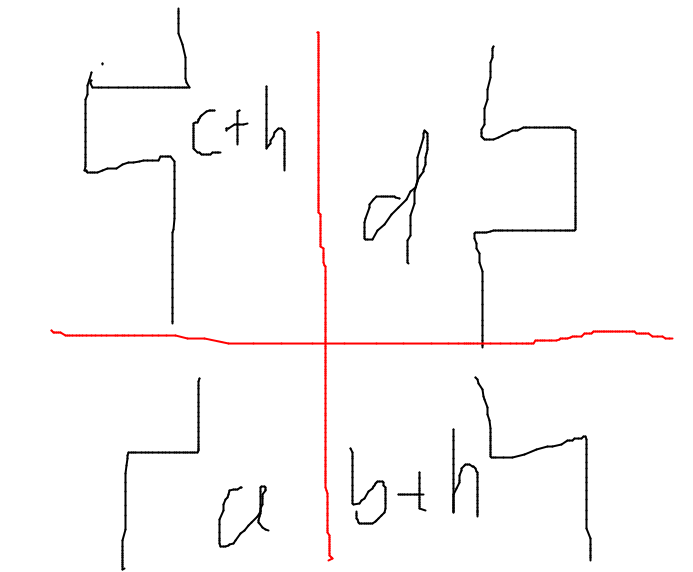
发现除了上文的信息其他信息都是冗余的。
每个转移相当于从上图中左边连向右边，表示放了一个积木。
这样就连出一张有向图。
同时，发现其实上图中下面两种图中可以无限连边，就是互不干扰都放在地上。
所以我们可以连无限条 \([h+1,h\times 2]\) 到 \([1,h]\) 的有向边。
然后需要找到一条从 \([1,h]\) 中某个点开始到 \([h+1,h\times 2]\) 中某个点结束的欧拉路。
发现除了最后连的边之外，入度出度已经确定了，所以可以设置一个无限源，表示连的边。
然后考虑再加一条边，最后一条边从终点连向起点，那就构成了一个欧拉环。
欧拉环可以直接判断入度等于出度且联通。

注意一个 corner case 就是如果初始就是一个欧拉环，就无解了。
因为我们找不到一个起点和一个终点满足它们不同。

Coding.

点击查看代码

//是啊，你就是那只鬼了，所以被你碰到以后，就轮到我变成鬼了{{{
#include<bits/stdc++.h>
using namespace std;typedef long long ll;
template<typename T>inline void read(T &x)
{
	x=0;char c=getchar(),f=0;
	for(;c<48||c>57;c=getchar()) if(!(c^45)) f=1;
	for(;c>=48&&c<=57;c=getchar()) x=(x<<1)+(x<<3)+(c^48);
	f?x=-x:x;
}
template<typename T,typename...L>inline void read(T &x,L&...l) {read(x),read(l...);}//}}}
struct edge{int to,nxt;}e[300005];int et,head[405],n,h,id[405],od[405],fa[405];
inline void adde(int x,int y) {e[++et]=(edge){y,head[x]},head[x]=et,id[y]++,od[x]++;}
inline int lftid(int a,int c) {return c?c+h:a;}
inline int rghid(int b,int d) {return d?d:b+h;}
inline int getf(int x) {return fa[x]==x?x:fa[x]=getf(fa[x]);}
inline void mrg(int x,int y) {x=getf(x),y=getf(y);if(x^y) fa[x]=y;}
int main()
{
	read(n,h);for(int i=1,a,b,c,d;i<=n;i++) read(a,b,c,d),adde(lftid(a,c),rghid(b,d));
	for(int i=1;i<=h;i++) if(od[i]<id[i]) return puts("NO"),0;
	for(int i=h+1;i<=h+h;i++) if(id[i]<od[i]) return puts("NO"),0;
	int c1=0;for(int i=1;i<=h;i++) c1+=od[i]-id[i];
	int c2=0;for(int i=h+1;i<=h+h;i++) c2+=id[i]-od[i];
	if(!c1||!c2) return puts("NO"),0;
	for(int i=1;i<=h;i++) for(int j=od[i]-id[i];j;j--) adde(h*2+1,i);
	for(int i=h+1;i<=h+h;i++) for(int j=id[i]-od[i];j;j--) adde(i,h*2+1);
	if(id[h+h+1]!=od[h+h+1]) return puts("NO"),0;else for(int i=1;i<=h+h+1;i++) fa[i]=i;
	for(int x=1;x<=h+h+1;x++) for(int i=head[x];i;i=e[i].nxt) mrg(x,e[i].to);
	int ls=0;for(int i=1;i<=h+h+1;i++) if(head[i]) {if(!ls) ls=getf(i);else if(ls^getf(i)) return puts("NO"),0;}
	return puts("YES"),0;
}