Preface
对于许多数论问题,都需要涉及到Gcd,求解Gcd,常常使用欧几里得算法,以前也只是背下来,没有真正了解并证明过。
对于许多求解问题,可以列出贝祖方程:ax+by=Gcd(a,b),用Exgcd解之即可到答案,Exgcd即扩展欧几里得算法。他还能求乘法逆元,同余方程通解。没有你想得到的,只有你做不到的。
这里是对于两个算法的学习小记
Content
欧几里得算法
算法介绍
由百度百科得
欧几里德算法又称辗转相除法,用于计算两个正整数a,b的最大公约数。
从整数的除法可知:对任给二整数a,b0,必有二整数q及r存在,使得a=qb+r,0≤rb,并且q及r是唯一存在的,这是数论的一条基本定理,整数的一系列重要性质都可以由此得到,如果反复利用这一基本定理,就可以得到因为每进行一次除法,余数就至少减一,而b是有限的正整数,所以最多进行b次,总可以得到一个余数是零的等式,即rn+1=0。
当然,百度说的这种话我都是看不懂的。
其实辗转相除法就是运用了Gcd(a,b)=Gcd(b,a mod b),直到a≡0(mod b),b即为所求。
这个方法的目的是为了达到可以将求解的两个数不断缩小,使得效率为对数级别。
算法证明
那么,我们如何求证这个式子的正确性呢?
我们令
![]()
根据模运算的定义,可以有
![]()
移项可得
![]()
令d为a,b公约数,可有
![]()
根据我的思考,得出拥有公约数的两个数相减,其差必定能整除这个公约数,用乘法分配律易证。由这个东东,我们知道d一定是a,kb的公约数,故可得
![]()
![]()
综上所瞎BB,因为d|b,d|a mod b,所以b和a mod b有公约数d,又因为d为a,b公约数,所以a,b,a mod b都包含约数d
上面的d为任意一个,当d为a,b的最大公约数,根据上面所说,此时b和a mod b一定也包含公约数d
算法实现
自此,我们证了欧几里得几千年前就会证的东西。用现代化语言来描述这古老的知识是这样的

扩展欧几里得算法
算法简介
按照惯例,看看大佬们怎么说。由百度百科得
扩展欧几里得算法是欧几里得算法(又叫辗转相除法)的扩展。除了计算a、b两个整数的最大公约数,此算法还能找到整数x、y(其中一个很可能是负数)。通常谈到最大公因子时, 我们都会提到一个非常基本的事实: 给予二整数 a 与 b, 必存在有整数 x 与 y 使得ax + by = gcd(a,b)。有两个数a,b,对它们进行辗转相除法,可得它们的最大公约数——这是众所周知的。然后,收集辗转相除法中产生的式子,倒回去,可以得到ax+by=gcd(a,b)的整数解。
这篇百度百科用了列式子,作诠释的说明方法,让我明白了许多,表达了作者写时凉凉的心情。
自从会证欧几里得算法之后,这一切的一切变得更加明朗蒙蔽
说白了,扩展欧几里得就是扩展的,运用某些欧几里得算法的东西来解出关于x,y的方程ax+by=gcd(a,b)的通解。但是一般没有几个身体健康的出题人会让你求这个无聊的东西。所以这个东西一般应用于求方程的某个特殊解亦或者求乘法逆元。
算法核心
我们看看它是怎么操作的,显然有
![]()
我们令,显然等于我头上的这个式子
![]()
我们将上面左式根据模定义升级得到
![]()
我们将y′代进括号里,再提取b,得
![]()
我们再看看上面的连等式ax+by,他们是等价的,根据恒等定理有
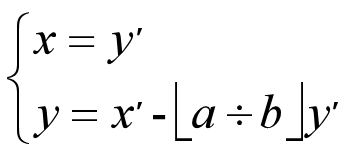
但是我们知道这个有什么用呢?我们又不知道他们其中任何一个值,根本求不出x和y。
我们需要冷静一下,x,y是在ax+by=Gcd(a,b)时的解。x′,y′是在gcd(b,a mod b)=bx′+(a mod b)y′时的解,那么
这既然是扩展的,必定与欧几里得有不可告人的关系。gcd在最后是当gcd(a,0)=a时,求出最大公约数。那么当b=0时,我们带进去ax+by=Gcd(a,b)里面算,其实就是ax=a,那么x必定为1.b不可知,我们可以将b视为0,那么此时x,y的一个解就是

我们既然知道了这个,我们根据上面x,y与x′,y′的关系式,推算出x,y的值,不断递归回去,继而得出满足贝祖方程的一个解。因为这个方程必定有规律可循,所以我们对这个解进行某些变换,即可得出这个方程的通解,这是显然又必然的。
算法实现
实现起来和欧几里得算法有异曲同工之妙,可以说我们比欧几里得厉害,因为他不会编程;

算法扩展
扩展一:乘法逆元
对于形如这个样的式子,我们称x是a关于b的乘法逆元
![]()
这个式子的本质就是
![]() 脑补得到
脑补得到
![]()
如果这个式子有关于x,y的整数解,那么a,b 必定互质。为什么?
如果a,b不互质,那么他们必定有公约数。那么根据上面所说,拥有公约数的两个数相减,其差必定能整除这个公约数,然而1并不是一个大于1的公约数,所以得证。
因为y是未知的,我们可以将y视为相反数,那么符号可以变为正,而扩展gcd又可以解负数,其颜值越来越像贝祖公式了。又因为gcd(a,b)=1,所以得到
![]()
一不小心又可以用扩展欧几里得来解了。显然可以求出x的值,x的值即为乘法逆元。对于这种a,b互质的同余方程,一般只有唯一解。当然,会有无解的情况。根据一个定理来判断:ax+by=c,那么gcd(a,b)丨c,不然的话无解。
扩展二:求解方程ax+by=c
这个与上面类似。因为gcd(a,b)丨c,所以我们可以用扩展欧几里得先求出ax+by=gcd(a,b)
如何求目前这个方程的通解?假设我们求出了对于关于x,y的方程ax+by=gcd(a,b)的一组解为x0,y0,我们带入可以得到
ax0+by0=gcd(a,b),继而还有a(x0+b)+b(y0-a),a(x0+2*b)+b(y0-2*a),因为这样乘出来还是ax0+by0,所以可行
所以通解为x=x0+k*b;y=y0-k*a;
我们再看回原来的方程ax+by=c,发现其实类似,可以自己思考。
经典例题
[ZJOI2002] 青蛙的约会 →题解
[Vijos1009] 清帝之惑之康熙 →题解
[NOIP2012] 同余方程 →题解
[poj2115] C Looooops →题解
[poj2891] Strange Way to Express Integers →题解
[hdu1573] X问题 →题解
[hdu3579] Hello Kiki →题解
[poj2142] 天平 The Balance →题解
[poj1091] 跳蚤 →题解
[bzoj2242][SDOI2011]计算器