PCA算法
主成分分析(Principal Component Analysis,PCA)是最常用的一种降维方法,通常用于高维数据集的探索与可视化,还可以用作数据压缩和预处理等。PCA可以把具有相关性的高维变量合成为线性无关的低维变量,称为主成分。主成分能够尽可能保留原始数据的信息。PCA的计算涉及到对协方差矩阵的理解,这篇博客提供了协方差矩阵的相关内容。PCA的算法过程:

直接用numpy实现PCA
import numpy as np n = 2 # 取对应特征值最大的n个特征向量 data = np.random.rand(10, 5) # 生成10个样本,每个样本5个特征 mean = np.mean(data, axis=0) # 计算原始数据中每一列的均值,axis=0按列取均值 zeroCentred_data = data - mean # 数据中心化,使每个feature的均值为0 covMat = np.cov(zeroCentred_data, rowvar=False) # 计算协方差矩阵,rowvar=False表示数据的每一列代表一个feature featValue, featVec = np.linalg.eig(covMat) # 计算协方差矩阵的特征值和特征向量 index = np.argsort(featValue) # 将特征值按从小到大排序,index是对应原featValue中的下标 n_index = index[-n:] # 取最大的n个特征值在原featValue中的下标 n_featVec = featVec[:, n_index] # 取最大的两维特征值对应的特征向量组成映射矩阵 low_dim_data = np.dot(zeroCentred_data, n_featVec) # 降维后的数据
下图可帮助理解:
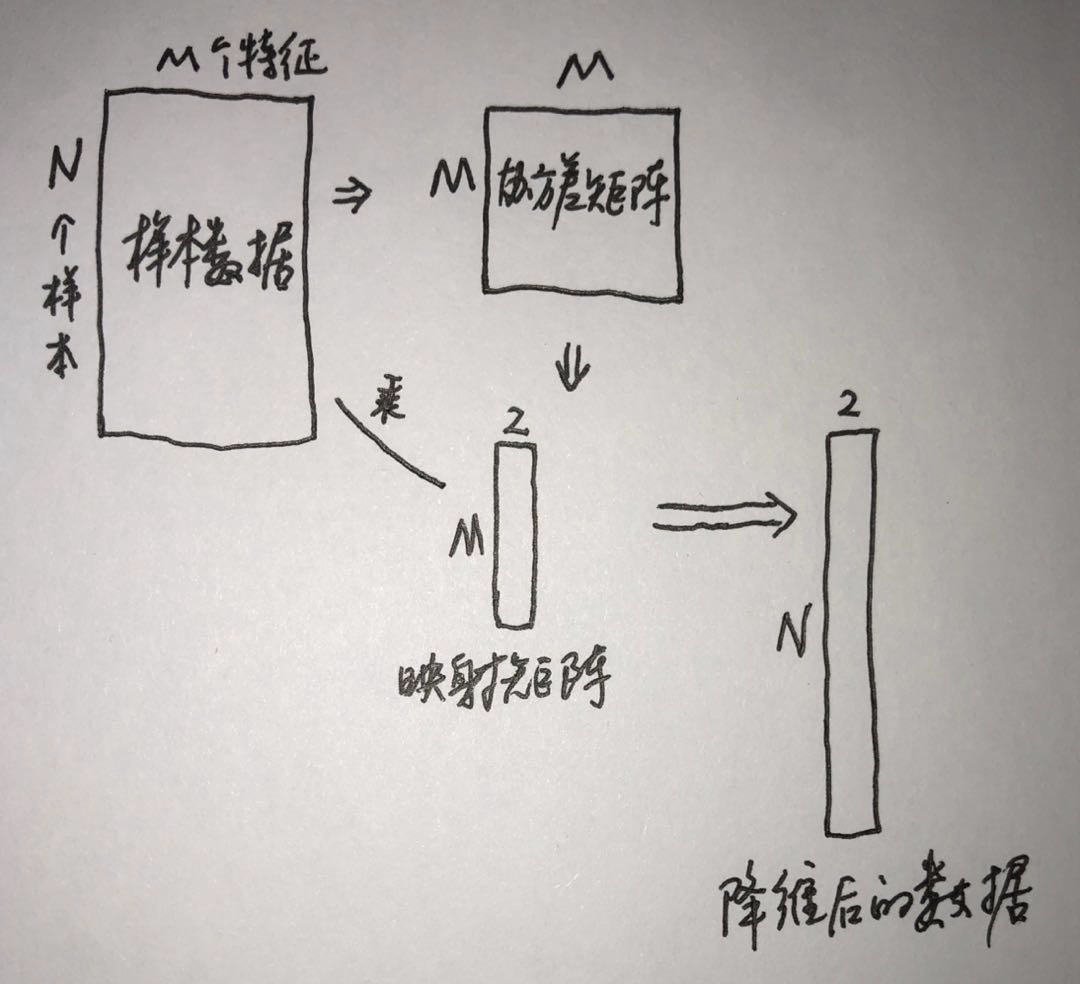
调用sklearn库实现PCA
这篇博客介绍了sklearn中PCA函数的具体参数。
import numpy as np from sklearn.decomposition import PCA data = np.random.rand(10, 5) # 生成10个样本,每个样本5个特征 pca = PCA(n_components=2) low_dim_data = pca.fit_transform(data) # 每个样本降为2维
参考资料
[1] Python机器学习应用