次梯度算法小实例

在上一篇博客中，我们介绍了次梯度，本篇博客，我们将用它来求解优化问题。

优化目标函数：

$min frac{1}{2} ||Ax-b||_2^2+mu ||x||_1$

已知$A, b$，设定一个$mu$值，此优化问题表示用数据矩阵$A$的列向量的线性组合去拟合目标向量$b$，并且解向量$x$需要尽量稀疏(因为L1范数限制)。

目标函数的次梯度$g$为：

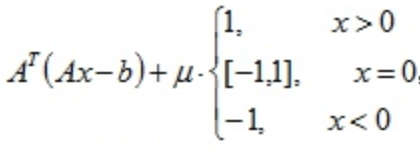
次梯度迭代算法：$x_{k+1} = x_k -  frac{alpha g}{sqrt{g^Tg}}$，下面代码中我们取系数$alpha=0.01$，但是张贤达的《矩阵分析与应用》第四章第5节第4小节指出，序列${alpha_k}_{k=0}^infty$必须递减：$k ightarrow infty, alpha_k ightarrow 0$. 下面的代码实践中，我们发现$alpha$一直取0.01，目标函数也能收敛。

需注意的是，次梯度算法不属于梯度下降法，因为次梯度算法不能保证$f(x_k)<f(x_{k-1})$。

代码实现：

import numpy as np
import matplotlib.pyplot as plt

m = 64
n = 128
A = np.random.randn(m, n)  # 随机生成数据矩阵
b = np.random.randn(m, 1)  # 随机生成目标向量
epoch = 150
v = 5e-1  # v为题目里面的mu
y = []

def f(x):
    '''目标函数'''
    return 1/2*np.dot((np.dot(A, x)-b).T, (np.dot(A, x)-b)) + v*sum(abs(x))

def g(x):
    '''次梯度，L1范数的次梯度直接用符号函数代替'''
    return np.dot(np.dot(A.T, A), x) - np.dot(A.T, b) + v*np.sign(x)

x0 = np.zeros((n, 1))  # 初始化解向量x
for i in range(epoch):
    y.append(f(x0)[0, 0])   # f(x0)是二维数据
    grad = g(x0)
    s = 0.01/np.sqrt(np.dot(grad.T, grad))
    x1 = x0 - s[0]*grad
    x0 = x1

plt.plot(range(epoch), y)
plt.show()

运行结果：

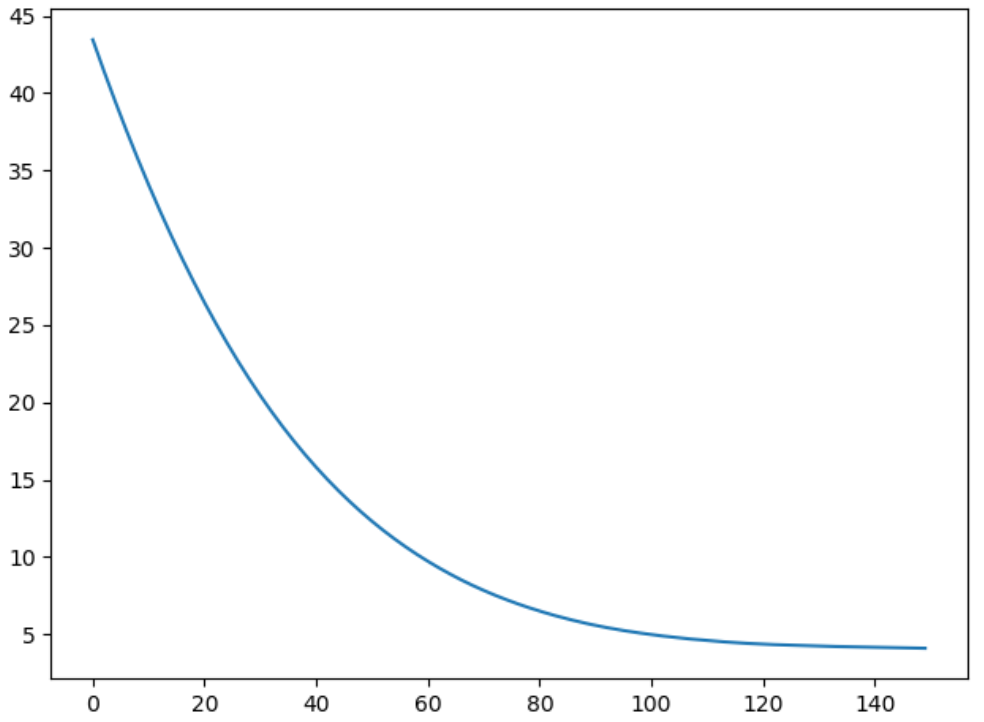
可以看到，收敛效果不错。

 -------------------------------------------------------------------------------------------------------------------------------

$mu$值的影响分析

目标函数中，第一项衡量拟合的质量，第二项衡量解向量$x$的稀疏程度，$mu$值平衡这两项的重要性，改变$mu$值，对解向量有一定影响：

   

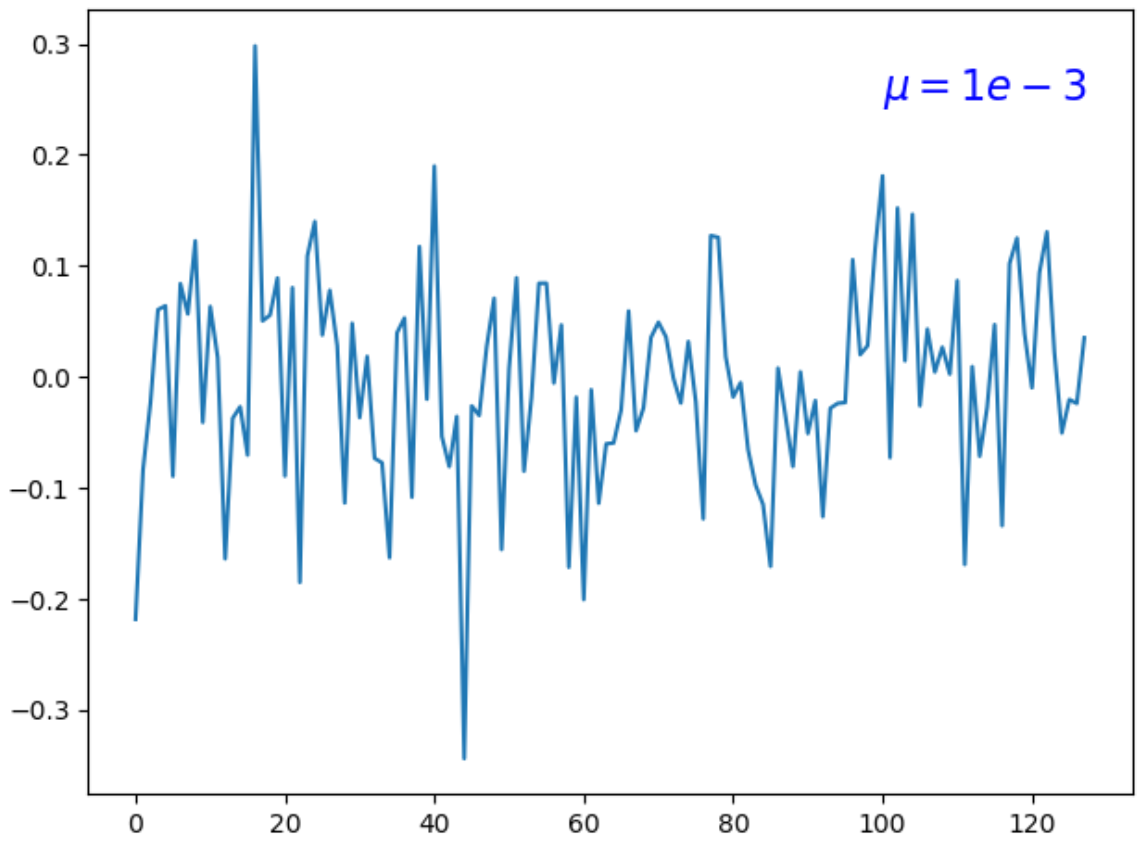
这两个图是解向量$x=(x_1, x_2, ..., x_{128})$的值图，比较这两图可以看到，$mu$越大，解向量$x=(x_1, x_2, ..., x_{128})$越多分量为零，即越稀疏。

参考资料：subgradient(次梯度算法)