1、哈夫曼树是啥啊?好吃吗?
(emmmm)先介绍一下哈夫曼树是个什么东西……哈夫曼树是一个有堆性质的多叉树,满足的性质是对于所有(f)的子节点(s)而言$$sumlimits_{s in f}^{}{v_s}=v_f$$。
停停停这不就是个简单的维护子节点的点权和嘛?
(⊙o⊙)…并不是,因为在哈夫曼树中,牵扯到动态连续决策生成祖先节点这么个东西…意思就是你现在有一堆节点,若你需要对他们进行建(k)叉哈夫曼树的操作,则每次会选择(k)优先级最小的节点,通过一些带有结合性地正增长运算,合并成一个节点,这个节点会重新回到原序列中,这样不断进行选点,会得到一棵树,保证根节点一定是所有节点的权值和。
说白了就是选一堆数里的(k)小个数合并起来再扔到这堆树里,直到剩下 一个位置(那我上面BB那么多干啥
(emmm)不大清楚?其实你可以结合竞赛树的性质思考一下,竞赛树的父节点都源自于子节点,但是竞赛树满足的是(min/max)的性质,而哈夫曼树则是(sum),其实类比一下也可以得到,对于有结合性质的运算都是可以用树的形式实现出来、比如最简单的异或运算(^)、或运算((|))以及与运算((&)),当然还可以拓展到更多,譬如积性函数(phi(x)),虽然不是完全积性函数,但是也可见一斑。
嗯,没准可以在树上子集合变换一下
但是很重要的一点是,在构造一棵哈夫曼树时,必须满足单调构造。
例如下图就是一棵对于数列(mathcal{1,2,3,6,12,4})的二叉哈夫曼树:
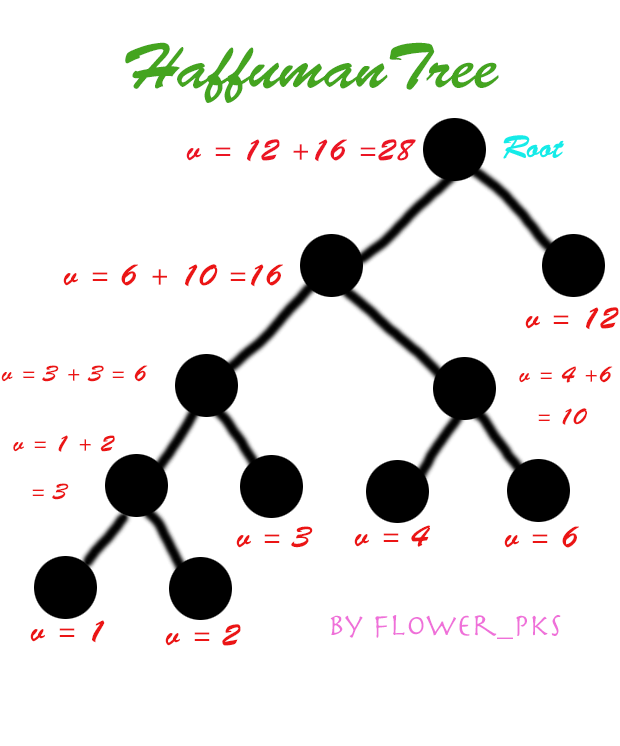
(画这图花了我老长时间OTZ果然我还是弱啊
那么这棵树的构造顺序就是:(1 + 2 => 3(aft), 3 + 3(aft) =>6(aft), 6 + 4 = 10, 6(aft) + 10 => 16(aft) , 16 + 12 = 28(aft))
2、那么从二叉哈夫曼树的代码开始讲起
首先很显然……这个这个我们既然要单调地选节点,就要用到堆这个数据结构 —— 我们可以考虑每次取出两个堆顶元素,合并之后再放回堆中……没有任何操作难度,对吧?
while(q.size()>1){
NODE s=p0;
for(int i=1;i<=2;i++){
NODE b=q.top(); q.pop();
ans+=b.w; s.w+=b.w;
}
q.push(s);
}
但是问题是这种智障操作的复杂度是(O(nlog_2n imes k))的,这个(k)是一个在不开O2的条件下的巨大常数。跑1e5的那种zz数据自然问题不大,但是一旦大于1e6就会很危险,所以我们试着优化它的常数以及基础时间复杂度。
我们考虑,如果对于这个策略组合,我们令其单调,那么我们只需要两个队列即可。一个队列用来存储叶子节点,另一个用来存储所有的父亲节点。每次取结点时,从两个队列的队首取节点。而因为其单调,所以正确性是显然的。(However),我们为了让其单调,一开始便需要排一遍序。但是排序的时间复杂度还是(O(nlog_2n)),所以并没有什么卵用。(常数小了呀
但是一旦我要执行(n)次甚至更多次对于同一数列,只不过(k)不同的操作时,这个算法的优化性一目了然。对于朴素的堆算法,如果执行(n)次,我们的时间复杂度是(O(n^2log^2n))的,但是FIFO队列的算法,我们的渐进时间复杂度为(O(n^2)),有了很大的优化。
那么他的代码是这样子的:
#define rep(a, i, b) for(long long i=a;i<=b;i++)
now = 0;
rep(1, j, 2){
if ((qv[r1] <= fa[r2] && qv[r1] != -1 ) || fa[r2] == -1){
ans += qv[r1] ;
now += qv[r1 ++ ] ;
}
else
if ((qv[r1] >= fa[r2] && fa[r2] != -1 ) || qv[r1] == -1){
ans += fa[r2] ;
now += fa[r2 ++] ;
}
}
fa[++ r] = now ;
那么对于(k)叉哈夫曼树而言,由于我们并不能保证这(n)个节点可以不断取(k)个,因为你有可能会发现到了最后一次你会剩下不足(k)个节点。那么这是我们就需要在这之前先补上几个节点,权值为0的空节点。那么需要补多少个呢?我们这样想,每次取走((k - 1))个(取走k个还回来1个),一共要取走((n - 1))个节点,那么我们就只需要判断$$(n - 1)mod(k - 1) = 0 ?$$即可,缺(w)个就补上$(k-1) - w $个,然后合并即可。
tot = (n - 1) % (k - 1) ;
if(tot) tot = k - 1 - tot ;