Problem A. 最近公共祖先 (commonants.c/cpp/pas)
注意
Input file: commonants.in
Output file: commonants.out
Time Limit : 0.5 seconds
Memory Limit: 512 megabytes
题面
最近公共祖先( ext{(Lowest Common Ancestor,LCA)})是指在一个树中同时拥有给定的两个点作为后
代的最深的节点。
为了学习最近公共祖先,你得到了一个层数为(n+1)的满二叉树,其中根节点的深度为(0),其他节点的深度为父节点的深度(+1)。你需要求出二叉树上所有点对 ( exttt{(i,j)}),((i),(j)可以相等,也可以(i > j))的最近公共祖先的深度之和对(10^9+7)取模后的结果。
输入格式
一行一个整数(n)。
输出格式
一行一个整数表示所有点对 ( exttt{(i,j)}),((i),(j)可以相等,也可以(i > j))的最近公共祖先的深度之和对(10^9+7)取模后的结果。
样例
( exttt{input#1})
2
( exttt{input#2})
19260817
( exttt{output#1})
22
( exttt{output#2})
108973412
数据范围与提示
样例(1)解释:
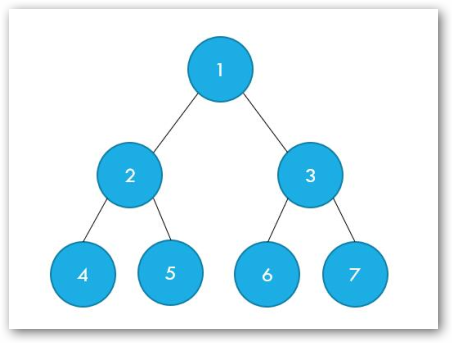
树一共有(7)个节点(一个根节点和两个子节点),其中 ( exttt{(4,4),(5,5),(6,6),(7,7)}) 共(4)对的最近公共祖先深度为(2),( exttt{(4,2),(2,4),(5,2),(2,5),(5,4),(4,5),(2,2),(6,3),(3,6),(3,7),(7,3),(6,7),})( exttt{(7,6),(3,3)})共(14)对最近公共祖先深度是(1),其他的点对最近公共祖先深度为(0),所以答案为(22)。
对于(20%)的数据,(n le 10)。
对于(50%)的数据,(n le 10^6) 。
对于(100%)的数据,(1 le n le 10^9) 。
题解
对于一颗有(n)层的满二叉树很显然符合以下几点
1.第(i)层的点的个数为(2^i)。
2.以第(i)层的点为根节点的子树大小为(2^{n-i+1}-1)。
3.以第(i)层的点为( ext{LCA})的点对个数为(2^{2n-i+1}-2^i)
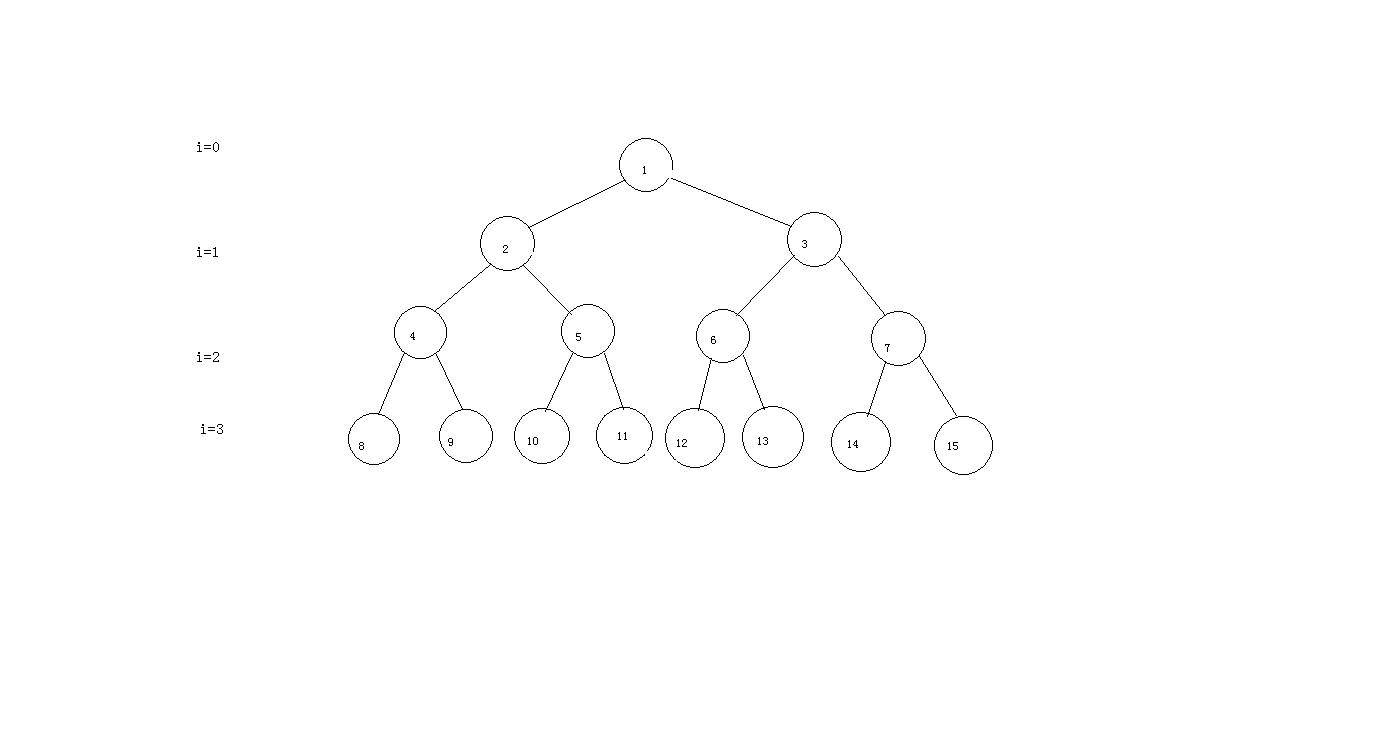
观察上面的图(好丑),很明显(1,2)都是对的。
对于一颗以第(i)层的节点为根的子树:
①它的左子树与右子树上的点的( ext{LCA})都为根节点。所以点对个数为
②这棵子树的左子树与根节点的( ext{LCA})都为根节点。右子树也是。所以有(2^{n-i+1}-2)对点。
③根节点与根节点的( ext{LCA})也是根节点,点对个数为1。
点对( exttt{(u,v)})与点对( exttt{(v,u)})在(u
eq v)时是两个不同的点对。
所以将上述①②相加乘二再加③就是以子树根节点为( ext{LCA})的点对的数量为:
因为第(i)层的点的个数为(2^i)。所以以第(i)层的点为( ext{LCA})的点对个数为:
因为一共有(n+1)层,从(0-n)层,所以答案为:
但这样复杂度为(Theta (nlog_n))过不了。。将上面的式子展开:
很明显前(n)项为等比数列,利用等比数列求和公式可以很快求出。
很明显也是等比数列。将这两个相加就是答案了。
快速幂是(log)。所以复杂度是(Theta(log_n))
(Code)
#include<bits/stdc++.h>
typedef long long ll;
ll n;
const ll mod=1000000007;
inline void read(ll &T) {
ll x=0;bool f=0;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=!f;c=getchar();}
while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();}
T=f?-x:x;
}
inline ll qpow(ll a,ll b) {
ll ans=1,base=a;
while(b) {
if(b&1) ans=(ans*base)%mod;
base=(base*base)%mod;
b>>=1;
}
return ans%mod;
}
int main() {
read(n);
ll qwq=(((2*qpow(2,2*n+1))%mod-qpow(2,n+2)+5*mod)%mod-n*qpow(2,n+1)+5*mod)%mod;
ll qaq=((((2*qpow(2,n))%mod)-2+5*mod)%mod-n*qpow(2,n+1)+5*mod)%mod;
//std::cout<<qwq<<'
'<<qaq<<'
';
std::cout<<(qwq+qaq+5*mod)%mod;//加上一个模数再取模是为了处理负数的情况
return 0;
}