可持久化Trie
题解:
可以用前缀数组O(1)解决区间异或的询问
[A_ioplus A_{i+1} oplus A_{i+2} oplus ... oplus A_j = (A_1 oplus A_2 oplus ... oplus A_j) oplus (A_1 oplus A_2 oplus A_3 oplus...oplus A_{i-1})
]
int arr[N]; // 原数组
int pre[N]; // 前缀异或数组
for(int i = 1; i <= n; i++){
scanf("%d",&arr[i]);
}
pre[1] = arr[1];
for(int i = 2; i <= n; i++){
pre[i] = pre[i-1] ^ arr[i];
}
对于题目的每一个Q询问,我们找到一个这样的p使得(p in [l,r]),且(A_p oplus A_{p+1} oplus ... oplus A_N oplus x)最大
我们可以通过刚才得到的前缀数组来将问题简化成找到一个这样的p使得(p in [l,r]),且pre[p-1] ^ pre[n] ^ x最大
而对于每一个独立的询问,pre[n] ^ x是固定不变的,不妨设y = pre[n] ^ x,因此我们最终的问题就是如何找到最优的p使得pre[p-1] ^ y 最大
我们从二进制的角度考虑这个问题. **是按位异或,我们要想找到最大的pre[p-1]y,肯定是基于贪心的思路,优先找高位异或为1的pre[p-1].不妨建立一颗01Trie来维护. 对于每一个给定的y,我们从01Trie**的树根和y的最高位开始,优先选择高位异或为1的结点.最终遍历到Trie的树根就可以得到最优答案.(这个贪心如果不理解,可以先做AcWing - 143 - 最大异或对)
接下来的问题是,如何使得p从[l,r]区间中进行选择?不妨由浅入深分析这个问题:
- 假设只询问(pin [1,n]),那么只需要最基本的Trie就可以维护了.
- 假设询问(pin[1,r] , r leqslant n),那么说明我们需要维护历史版本的Trie,这一点可以用可持久化Trie实现.
- 现在要询问(p in [l,r],)也就是说我们需要在历史版本为r的基础上,筛除版本在[1,l-1]的数.假设我们取出版本为r的Trie如下图所示.
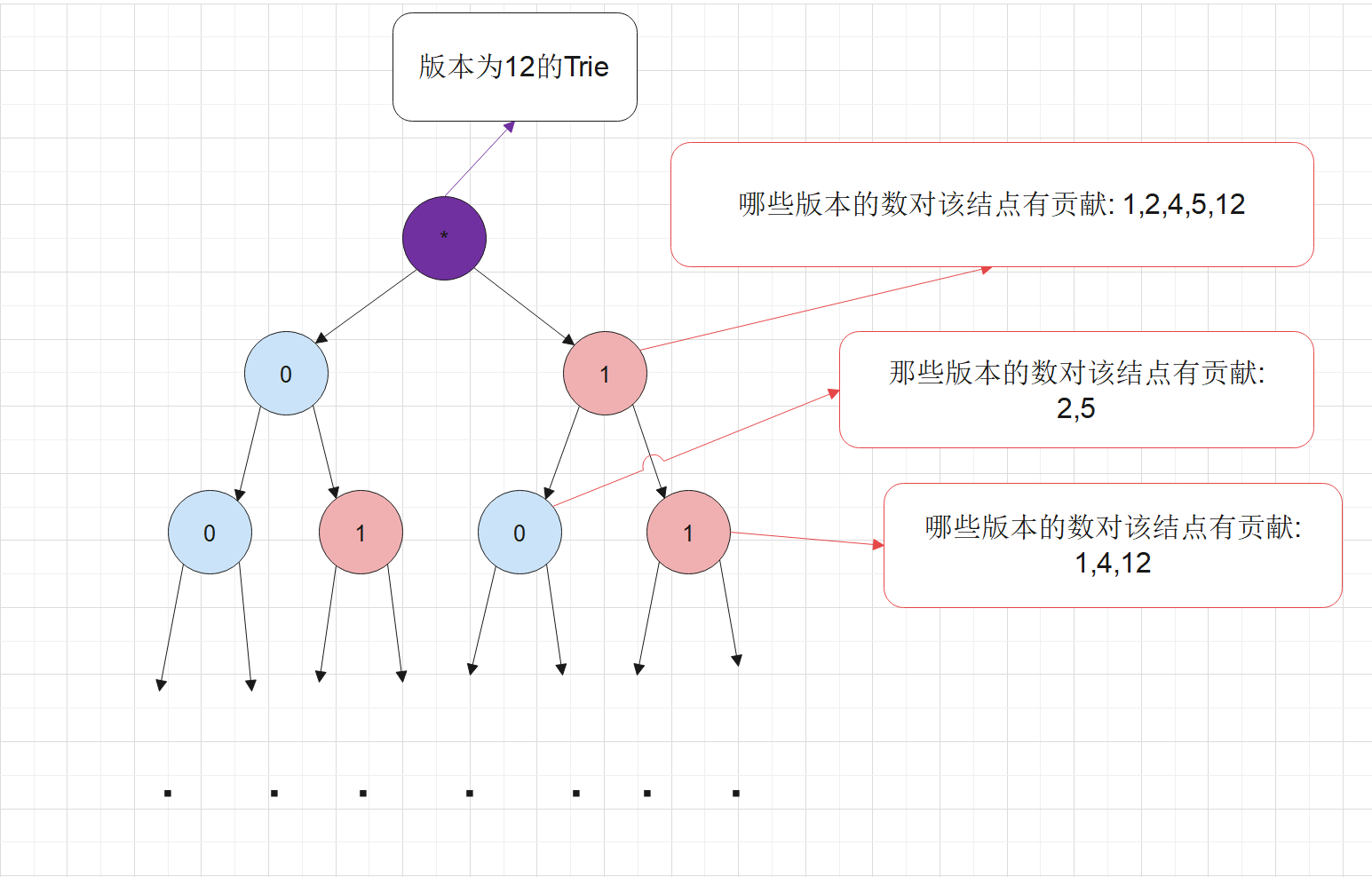
假设我们要求(p in [5,12]),那么对于每一个结点,至少出现一次5以上的版本我才能够访问这个结点. 这个问题等价于: 某个结点的最大历史版本号大于或等于5才能访问这个结点.因此,我们不妨对于每一个结点记录其最大历史版本号,就能够解决左端点的限制问题.
整理一下思路,我们的解题步骤为:
- 对于单次加点操作: 更新前缀异或数组 (复杂度为O(1)) 然后更新可持久化Trie,添加新版本(常数复杂度,32左右)
- 对于单次询问操作: 从r版本Trie树根开始,依次向下层深入,比较每个结点的最大版本号与l的大小,贪心.(常数复杂度,32左右)
因此整个算法的复杂度为O(n)级别,大概执行3e5 * 32次
#include <cstdio>
#include <cstdlib>
#include <vector>
using namespace std;
#define LENGTH 23
#define MAX(a,b) (a>b?a:b)
const int N = 6e5+10;
int len; // 当前版本号
int idx; // 索引分配器
int pre[N]; // 记录各个版本的前缀异或数组
int roots[N]; // 记录各个版本的树根
int maxTime[LENGTH*N];
int nex[LENGTH*N][2];
void insert(int x){ // 向字典树中加入一个值
pre[1+len] = pre[len] ^ x;
++len;
++idx;
roots[len] = idx;
maxTime[idx] = len;
int rt = idx;
int pos = 1 << LENGTH;
if(len == 1){ // 如果当前版本号为1
for(int i = LENGTH; i >= 0; i--){
++idx;
if(pre[len] & pos){
nex[rt][1] = idx;
rt = idx;
}else{
nex[rt][0] = idx;
rt = idx;
}
pos >>= 1;
maxTime[rt] = 1;
}
}else{
int flag = 1;
int oldRoot = roots[len-1];
for(int i = LENGTH; i >= 0; i--){
++idx;
if(pre[len] & pos){
nex[rt][1] = idx;
if(flag){
nex[rt][0] = nex[oldRoot][0];
oldRoot = nex[oldRoot][1];
if(!oldRoot){
flag = 0;
}
}
rt = idx;
}else{
nex[rt][0] = idx;
if(flag){
nex[rt][1] = nex[oldRoot][1];
oldRoot = nex[oldRoot][0];
if(oldRoot == -1){
flag = 0;
}
}
rt = idx;
}
pos >>= 1;
maxTime[rt] = len;
}
}
}
int query(int l,int r,int x){
x ^= pre[len];
int pos = 1 << LENGTH;
int v = 0;
int rt = roots[r];
for(int i = LENGTH; i >= 0; i--){
if(x & pos){
if(nex[rt][0] && maxTime[nex[rt][0]]>= l){
v <<= 1;
rt = nex[rt][0];
}else{
v <<= 1;
v |= 1;
rt = nex[rt][1];
}
}else{
if(nex[rt][1] && maxTime[nex[rt][1]] >= l){
v <<= 1;
v |= 1;
rt = nex[rt][1];
}else{
v <<= 1;
rt = nex[rt][0];
}
}
pos >>= 1;
}
return x ^ v;
}
int main(){
int n,m,l,r,temp;
char cmd[5];
scanf("%d%d",&n,&m);
for(int i = 1; i <= n; i++){
scanf("%d",&temp);
insert(temp);
}
for(int i = 1; i <= m; i++){
scanf("%s",cmd);
if(cmd[0]=='A'){
scanf("%d",&temp);
insert(temp);
}else{
scanf("%d%d%d",&l,&r,&temp);
l--;
r--;
if(r == 0){
printf("%d
",pre[len]^temp);
}else{
printf("%d
",query(l,r,temp));
}
}
}
system("pause");
return 0;
}