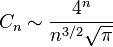下面是几篇关于卡特兰介绍的文章:
我在下面直接复制了下面几篇文章的内容(或多或少的copy),
关于卡特兰数(记不住组合公式的可以记住折线法,它是一种几何证明“计算出卡特兰数”)。
文章链接:
http://blog.csdn.net/sabers_master/article/details/77711648
http://blog.sina.com.cn/u/1885661061
http://www.cnblogs.com/code-painter/p/4417354.html
http://blog.sina.com.cn/s/blog_6917f47301010cno.html (折线法证明卡特兰数)
1.什么是卡特兰数:
卡特兰数是一种经典的组合数,经常出现在各种计算中,其前几项为 : 1,1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, …
2.卡特兰数的公式:
(1) h(n)= h(0) * h(n-1)+h(1) * h(n-2) + … + h(n-1)h(0) (n>=2)
(2) h(n)=h(n-1) * (4 * n-2)/(n+1)
(3) h(n)=c(2n,n)-c(2n,n-1)(n=0,1,2,…)
(4) h(n)=C(2n,n)/(n+1) (n=0,1,2,…)
3.卡特兰数的应用:
以下部分转自: 卡特兰数应用
1.出栈次序:
a.饭后,姐姐洗碗,妹妹把姐姐洗过的碗一个一个放进碗橱摞成一摞。一共有n个不同的碗,洗前也是摞成一摞的,也许因为小妹贪玩而使碗拿进碗橱不及时,姐姐则把洗过的碗摞在旁边,问:小妹摞起的碗有多少种可能的方式?
b.一个有n个1和n个-1组成的字串,且前k个数的和均不小于0,那这种字串的总数为多少?
c.P=A1A2A3……An,依据乘法结合律,不改变其顺序,只用括号表示成对的乘积,试问有几种括号化的方案?
d.n个人拿5元、n个人拿10元买物品,物品5元,老板没零钱。问有几种排队方式。
由于每个拿5元的人排队的次序不是固定的,所以最后求得的答案要 * n!。拿10元的人同理,所以还要 * n!。所以这种变种的最后答案为h(n) * n! * n!
2. n个节点的二叉树有多少种构型?
3. 有n+1个叶子的满二叉树的个数?

4. 在n*n的格子中,只在下三角行走,每次横或竖走一格,有多少中走法?

5. 将一个凸n+2边形区域分成三角形区域的方法数?

6. 在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?

7. n个长方形填充一个高度为n的阶梯状图形的方法个数?

8. 12个高矮不同的人,排成两排,每排必须是从矮到高排列,而且第二排比对应的第一排的人高,问排列方式有多少种?
上面一些问题有些是同构的,但有些却实在看不出联系来,他们的答案却都为卡特兰数。在《Enumerative Combinatorics》一书中,竟然提到了多达 66种组合问题和卡特兰数有关。
我们先来看看何为卡特兰数:
卡塔兰数的一般项公式为 
Cn的另一个表达形式为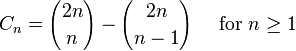
递归式:令h(0)=1,h(1)=1,catalan数满足递归式:
h(n)= h(0)*h(n-1) + h(1)*h(n-2) +  + h(n-1)h(0) (其中n>=2)
+ h(n-1)h(0) (其中n>=2)
另类递归式: h(n)=((4*n-2)/(n+1))*h(n-1);
前几项为 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...
卡塔兰数的渐近增长为