马尔科夫决策过程（MDP）

1.马尔科夫性

系统的下一个状态仅与当前状态有关，与以前的状态无关。

定义：状态s_t是马尔科夫的，当且仅当P[s_t+1|s_t]=P[s_t+1|s₁……s_t],当前状态s_t其实是蕴含了所有相关的历史信息，一旦当前信息已知，历史信息会被抛弃。

2.马尔科夫过程

    是一个二元组，包括状态机和状态转移概率。从某个状态出发到终止状态的过程链。不存在动作和奖励。

3.马尔科夫决策过程

    由元组（S，A，P，R，γ），P为状态转移概率，包含动作；γ为折扣因子，用来计算累计回报。

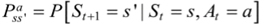
表示的是在当前s ∈ S状态下，经过a ∈ A作用后，会转移到的状态s’的概率分布情况。

4.几个重要函数

（1）策略函数：策略是指状态到动作的映射。策略的定义用条件概率分布给出。表示给定状态s时，动作集上的分布。强化学习是要找到最优策略，最优指的是总回报最大。

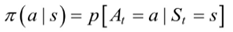
（2）累计回报：给定了策略之后就能计算累计回报了。

 

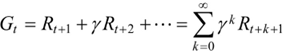
（3）状态值函数。由于策略π是随机的，所以求得的累计回报也是随机的。累计回报的期望是确定值，累计回报在状态s处的期望定义为状态值函数。

 

（4）状态-行为值函数：状态s下，选择行为a的期望值函数。

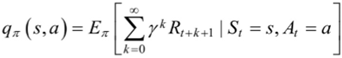
（5）状态值函数和状态-行为值函数的贝尔曼方程。

①状态值函数

 

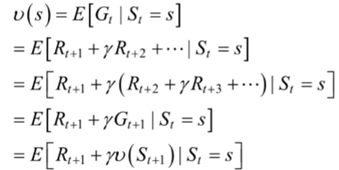
表示当前状态和下一状态的递归关系。

②状态-行为值函数

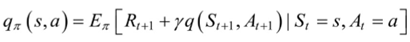
（6）状态值函数和状态-行为值函数之间的关系

给定当前状态s和当前动作a，在未来遵循策略π，那么系统转向下个状态s'的概率是

 

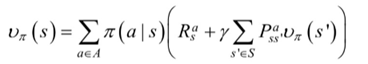
π(a|s)表示状态s对应不同的策略，P表示执行动作a后下一步的状态概率，R表示状态s下执行动作a得到的立即奖赏

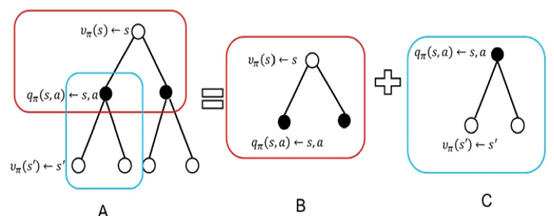
具体分析步骤如下图：

s→s’整个步骤分成两部分，B和C两部分。B部分为从s状态选择行为a的状态值函数为

 

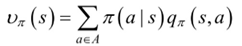
C部分给出了状态值函数和状态行为值函数的关系：

 

同理，用s’代替s，得到的状态值函数为：

 

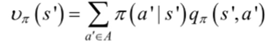
带入上面的状态行为值函数得到函数：

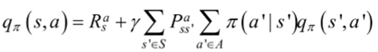
（7）策略π和初始状态s是我们给定的，当前的动作a也是我们给定的，这是q状态行为值函数和V状态值函数的主要区别

（8）计算值函数是为了构建学习算法，从数据中得到最优策略，最优策略对应着最优的状态值函数，所在策略中最大的值函数。