转载来自:http://blog.csdn.net/acdreamers/article/details/44662633
关于最小二乘问题的求解,之前已有梯度下降法,还有比较快速的牛顿迭代。今天来介绍一种方法,是基于矩阵求导来计算的,它的计算方式更加简洁高效,不需要大量迭代,只需解一个正规方程组。在开始之前,首先来认识一个概念和一些用到的定理。矩阵的迹定义如下
一个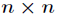 的矩阵
的矩阵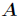 的迹是指
的迹是指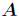 的主对角线上各元素的总和,记作
的主对角线上各元素的总和,记作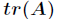 。即
。即





好了,有了上述7个定理,就可以来求最小二乘解了。设

那么进一步得到

接下来会涉及到矩阵求导,因为

那么进一步利用矩阵求导并利用上述定理,得到

我们知道在极值点处梯度值为零,即

上述得到的方程组叫做正规方程组,那么最终得到

这样最小二乘问题只需解一个线性方程组即可,不再需要像梯度下降那样迭代了。
既然说到了正规方程组,在介绍一种方程组,叫做超定方程组,它的定义为:把方程个数大于未知量个数的方
程组叫做超定方程组。通常来说,对于一个超定方程组 来说,求最小二乘解只需要两边同时乘
来说,求最小二乘解只需要两边同时乘 的转
的转
置,然后得到正规方程组 ,然后解这个方程就得到了最小二乘解。
,然后解这个方程就得到了最小二乘解。