（3）连续周期信号的傅里叶级数

《信号与系统（第二版）》 杨晓非 何丰

https://zhuanlan.zhihu.com/wille/19763358；

http://blog.sina.cn/dpool/blog/s/blog_57ad1bd20100txgs.html；

http://blog.renren.com/share/343320656/15540620254；

http://www.360doc.com/content/13/0328/12/202378_274443797.shtml；

http://jingyan.baidu.com/article/cbf0e500f1ce562eaa2893f4.html

直流分量和交流分量

任意信号f(t)可以分解为直流分和交流分量，该信号的直流分量就是该信号的几何平均值，是一个与事件无关的常数：

以T为周期的周期信号的直流分量为：

从周期信号中减去直流分量就可以得到信号的交流分量。

三角型傅里叶级数

正弦函数是简单的周期函数：y=Asin(wt+Φ)，其中周期为2π/w，A为振幅，w为角频率，Φ为初相位。

 要想研究非周期函数，先来讨论周期函数。可以将周期为2l的周期函数f(t)展开成简单的周期函数，例如三角函数组成的级数（这时候还不能叫做傅里叶级数）：

 

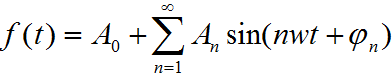
其中A₀表示f(t)的直流分量，A₁sin(wt+Φ)称为一次谐波（也叫基波），而A₂sin(2wt+Φ)称为二次谐波...等等。将A_nsin(nwt+Φ)完全展开后得到：

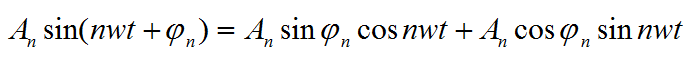
我们可以令A₀=a₀/2，A_nsinΦ_n=a_n ，A_ncosΦ_n=b_n，w=π/l，那么将这些带入公式可得：

 

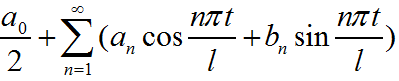
将πt/l=x,将式子整理得出：

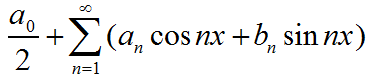
这样就得到了周期函数的三角函数级数。

傅里叶级数是一种频域分析工具，可以理解成一种复杂的周期波分解成直流项、基波（角频率为ω）和各次谐波（角频率为nω）的和，也就是级数中的各项。

为什么可以将周期信号分解成不同的简单正弦函数呢？下面看几幅图就比较清楚了：

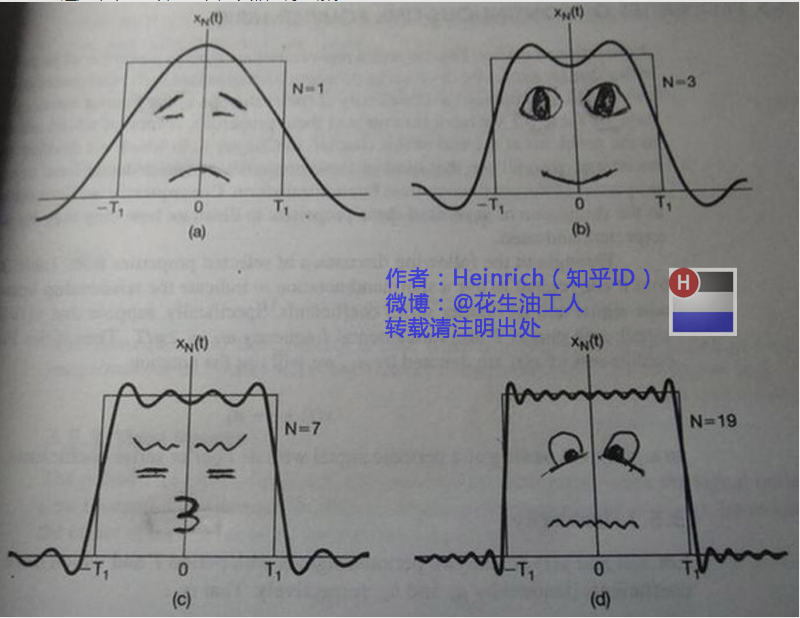
为了得到傅里叶级数，下面讨论三角函数系的正交性：

三角函数系：1，cosx，sinx，cos2x，sin2x，...，cosnx，sinnx，...

三角函数系在区间[-π，π]上正交，就是指三角函数系中任意不同的两个函数乘积在区间[-π，π]上的积分等于0，如下图

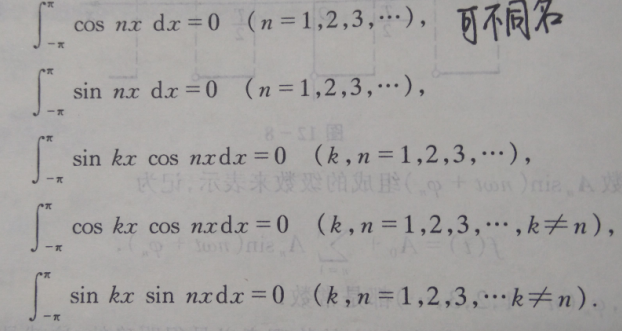
下面基于三角函数系讨论将函数展开成三角函数型傅里叶级数

指数型傅里叶级数

上面已经讨论了三角函数型的傅里叶级数，下面将该傅里叶级数进行变形，通过欧拉公式，改写成指数型傅里叶级数。

图中的圆形标记可以看出求和的上下限是1→无穷大，因为在三角函数型傅里叶级数中的频率是从基波（一次），二次，三次...依次进行累加。

 矩形框标记中显示了比较奇妙的思路：

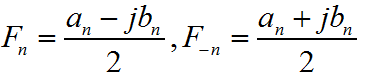
单独的一个F_ne^jmwt不能构成一个谐波分量，必须是F_ne^jmwt和F_-ne^-jmwt成对出现才能构成一个实际存在的谐波分量。负频率的出现仅仅是数学形式，实际并不存在。F_-n=F_n*是Fn的共轭负数，他们总是成对出现的。

 下面对Fn的求解进行解释说明，在解释之前先写出Fn的定义式：

其中对Fn的求解有两种求解方式，首先介绍第一种：

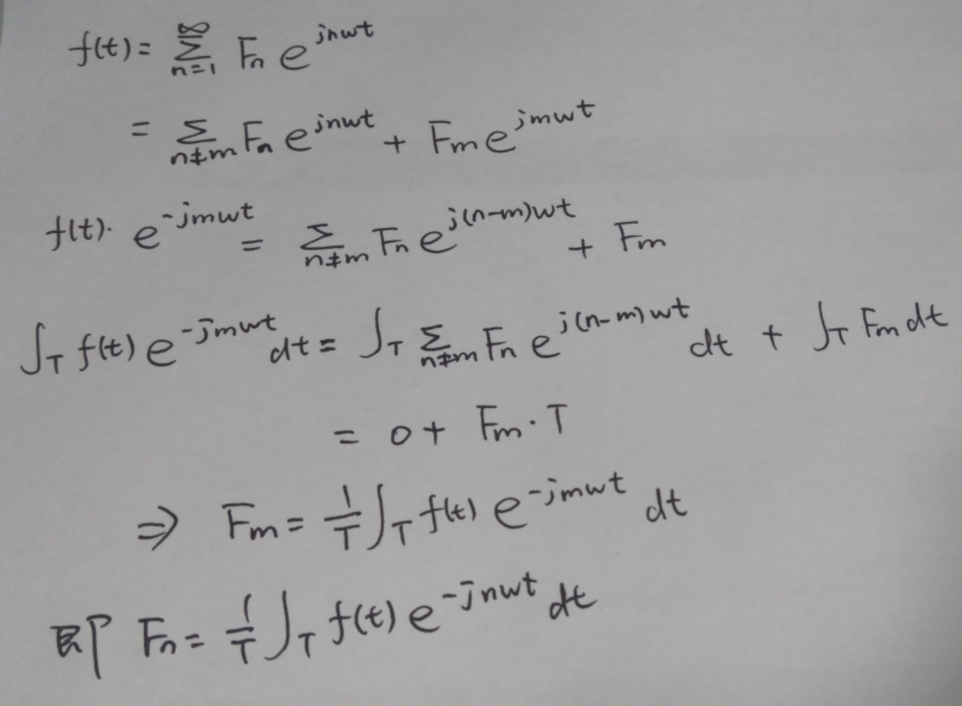
其次是第二种，将三角函数型的傅里叶级数的系数表达式代入指数型傅里叶级数进行求解，然后通过归纳法求解通式：

将已得到的结果进行合并写成：

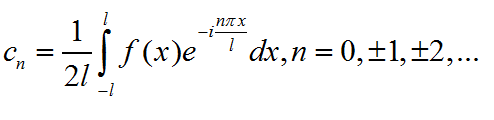
傅里叶级数之间的关系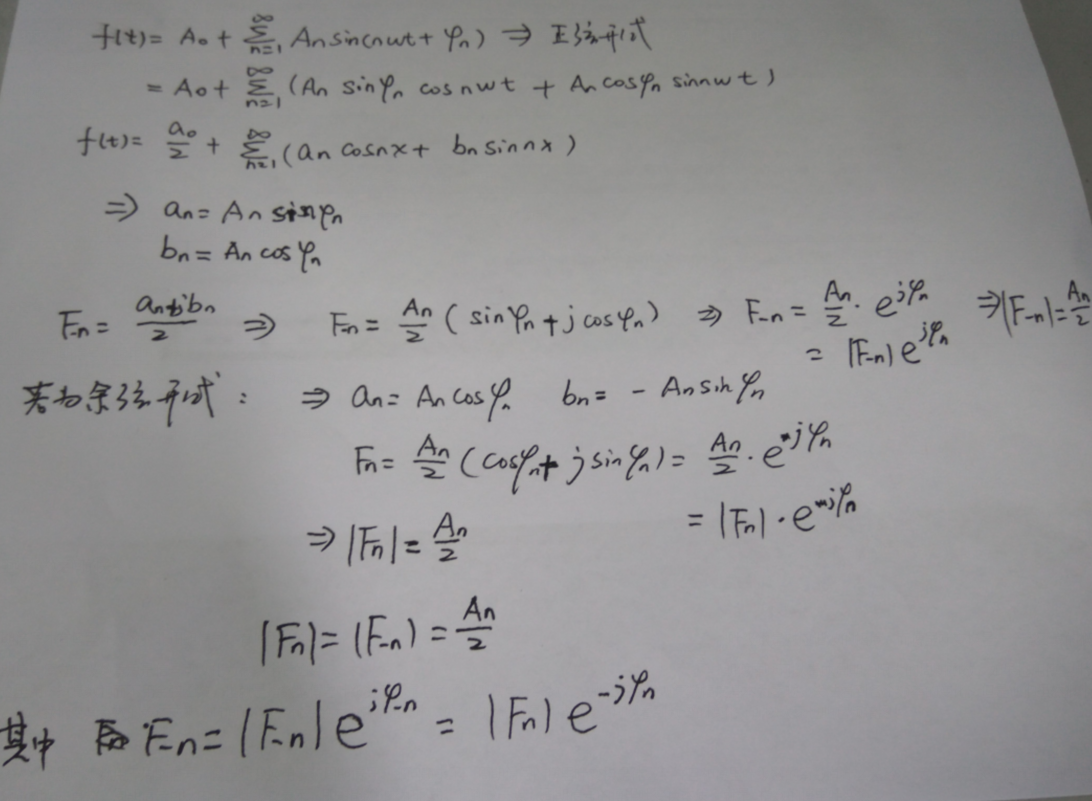

 另外|F_n|=|F_-n|是n的偶函数，Φ_n=-Φ_-n是n的奇函数。

微分冲激法求解傅里叶系数

微分冲激法的主要思路是将信号进行多次微分成冲激信号 ，然后根据时移性和时域微分性对傅里叶级数的影响，从而求解出原信号的傅里叶级数，因为冲激信号的傅里叶级数是固定不变的，可以通过定义求解出来。

--------------------------------------------------------------------------

欢迎访问图像计数项目总结：基于图像处理的毛毡垫计数项目总结

Github地址：Extract-inner-image