解数独小游戏的暴力算法以及c语言代码

数独（sudoku），是一个填数字的游戏，规则简单，上到老爷爷老奶奶，下至小学生，都可以去解它，放松益脑。

一直以来就特别喜欢数独，第一次是从老爸手机上看到的，也做过不少题目。在初中的时候上发过了一本书，书的后面就有一个数独的题目，我是班上第一个也是唯一一个解出来的，十分骄傲。

最近学习了算法，发现里面的n皇后问题和数独特别的相似，感觉都可以使用回溯法在解空间树经行广度优先搜索。这种方法类似于穷举法，但并不是单纯的列举全部可能，不断的有剪枝函数减去不满足条件的子树。看到网上说一种叫做跳舞链的方法，下面的代码并不是采用这种方法，以后如果有时间可以去试一试。而我使用的是回溯法，使用语言是c语言。闲话就说到这里，下面分析一下代码。

核心内容：树的深度优先遍历

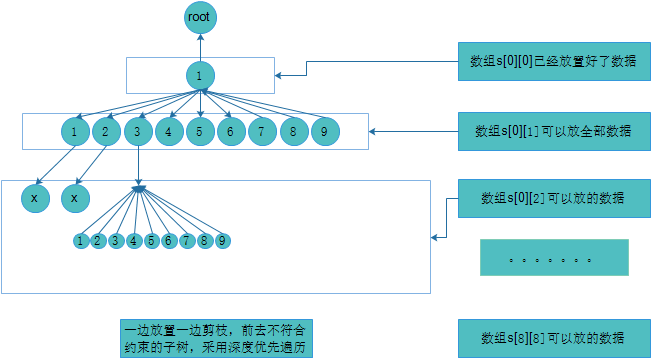
把数独想象成一个具有81层的树，然后在树上搜索剪枝。

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
//定义一个二维数组sudo[9][9]
 
 /*
int sudo[9][9]={
                    {    5,7,6,     -1,4,8,     1,3,-1},
                    {  -1,3,-1,    -1,-1,5,    -1,8,-1},
                    {   8,2,-1,     3,-1,9,    -1,-1,7},
            
                    {   1,-1,9,    -1,-1,-1,     -1,-1,8},
                    {   -1,-1,3,   5,9,1,      6,-1,-1},
                    {   7,-1,-1,    -1,-1,-1,   4,-1,1},
            
                    {   2,-1,-1,    1,-1,3,     -1,4,5},
                    {   -1,1,-1,    4,-1,-1,    -1,2,-1},
                    {   -1,4,7,     9,5,-1,     8,1,6,}    
            };
            */
    //测试数据1
    int sudo[9][9]={
                    {    1,0,0,    0,5,0,     0,0,0},
                    {   4,0,2,     0,0,1,      0,3,0},
                    {   8,0,0,     0,0,6,      0,1,0},
            
                    {   0,0,0,    0,1,7,     6,0,0},
                    {   0,0,6,      5,0,2,     4,0,0},
                    {   0,0,7,    4,6,0,   0,0,0},
            
                    {   0,4,0,    9,0,0,     0,0,1},
                    {   0,9,0,    6,0,0,     7,0,5},
                    {   0,0,0,     0,3,0,     0,0,0}    
            };
    
     
int backtrack(int s[9][9],int row,int col);
//使用回溯法对解空间数经行深度搜索该函数就是深度搜索的函数 

void showsudo();
//打印当前的数独中各个格子的值 

int place(int s[9][9],int t,int j);
//剪枝函数 

int justIsRepeatIN9(int s[9][9],int x,int y,int m,int n);
//剪枝函数中检查3*3小块合法的的函数 


//从二维数组的左上角开始，向右搜索
//row表示行号，col表示列号 
int backtrack(int s[9][9],int row,int col){
    
    if(row == 9)  
        return 1;
        //最后一个，在这之前是s[8][8];递归到最深处；成功返回 
     
    if(s[row][col] != 0){
        if(col == 8){
           row++;
           col=0;
        }
        else    
            col++;
        return backtrack(s,row,col);
    }//如果 s[row][col]本来就有数据，需要跳过 ，分析下一个 
    
    //  s[row][col]是空的，则放入1~9 
    for(int k=1;k<10;k++){ 
        s[row][col]=k;
        if(place(s,row,col)) {
            //判断是否合法，如果合法就分析下一个 
            if(col == 8){
                if(backtrack(s,row+1,0)){
                    return 1;
                  }
            }
             else{
                  if(backtrack(s,row,col+1)){
                      return 1;
                  }
             }    
        }    
        s[row][col] = 0;
        //在后面的某次中发现，所有的数都有冲突，则前面的数放错了，所以需要恢复 
    }
    //从1~9没有找到合适的数放入，之前的出错了 
    return 0;
}

//判断整个数独是否合法 
int place(int s[9][9],int t,int j)
{
    for(int i=0;i<9;i++)
    {
        if(s[t][i] == s[t][j] && i!=j){
            return 0 ;
        }//判断行上没有冲突     
        if(s[i][j] == s[t][j] && i!=t){
            return 0 ;
        }//判断列上没有冲突
    }
    
    //判断块中是否有重复的 
    int x=t%3;
    int y=j%3;
        /*
        00 01 02 
        10 11 12 
        20 21 22 
        */ 
    if(x == 0 && y == 0){
        if(justIsRepeatIN9(s,t,j,t,j)){
            return 1;
        }
        else{
            return 0; 
        }
    }
    
    if(x == 0 && y == 1){
        if(justIsRepeatIN9(s,t,j-1,t,j)){
            return 1;
        }
        else{
            return 0; 
        }
    }
    
    if(x == 0 && y == 2){
        if(justIsRepeatIN9(s,t,j-2,t,j)){
            return 1;
        }
        else{
            return 0; 
        }
    }
    
    if(x == 1 && y == 0){
        if(justIsRepeatIN9(s,t-1,j,t,j)){
            return 1;
        }
        else{
            return 0; 
        }
    }
    
    if(x == 1 && y == 1){
        if(justIsRepeatIN9(s,t-1,j-1,t,j)){
            return 1;
        }
        else{
            return 0; 
        }
    }

    if(x == 1 && y == 2){
        if(justIsRepeatIN9(s,t-1,j-2,t,j)){
            return 1;
        }
        else{
            return 0; 
        }
    }
    
    if(x == 2 && y == 0){
        if(justIsRepeatIN9(s,t-2,j,t,j)){
            return 1;
        }
        else{
            return 0; 
        }
    }
    
        if(x == 2 && y == 1){
        if(justIsRepeatIN9(s,t-2,j-1,t,j)){
            return 1;
        }
        else{
            return 0; 
        }
    }
    
        if(x == 2 && y == 2){
        if(justIsRepeatIN9(s,t-2,j-2,t,j)){
            return 1;
        }
        else{
            return 0; 
        }
    }    
}

int justIsRepeatIN9(int s[9][9],int x,int y,int m,int n){
    //判断一个九宫格中是否有重复的数
    //其中s是数组，x是起始的位置，y是起始是位置
    //因为之前的数据都是有序的，并不需要判断其他的是否合法，只要判断指定的数 
    //只要知道特殊的 
    //m,n是需要判断的内容 
    for(int i=0;i<3;i++){
        for(int j=0;j<3;j++){
            if(s[x+i][y+j] == s[m][n] && x+i != m && y+j != n){
                return 0;
            } 
        }
    }
    return 1;
}
 
 //打印数独中各个格子的值 
 void showsudo()
 {
     for(int i=0;i<9;i++){
        for(int j=0;j<9;j++)
        {
            printf("%2d  ",sudo[i][j]) ;
            if(j%3 == 2)
            {
                printf("  ");
            }
         } 
        printf("
");
        if(i%3 == 2){
            printf("
");
        }
     }
    printf("
"); 
 }
 
 int main()
 {
     showsudo();
     backtrack(sudo,0,0) ;
     showsudo();
     return 0;
 }