图的m着色问题

图的m-着色判定问题——给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色，每个顶点着一种颜色，是否有一种着色法使G中任意相邻的2个顶点着不同颜色?

图的m-着色优化问题——若一个图最少需要m种颜色才能使图中任意相邻的2个顶点着不同颜色，则称这个数m为该图的色数。求一个图的最小色数m的问题称为m-着色优化问题。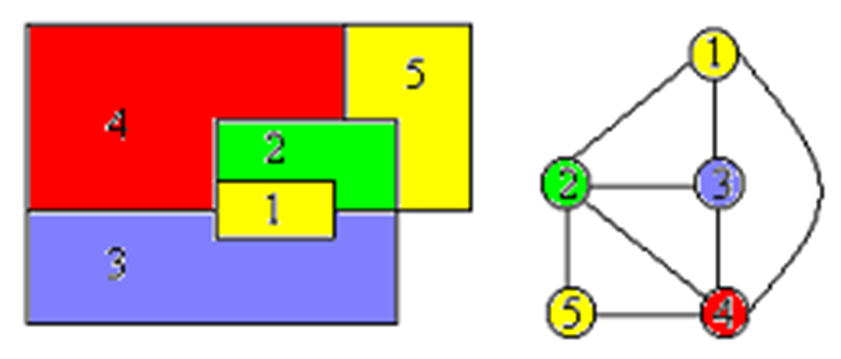

算法描述（迭代算法）

 color[n]存储n个顶点的着色方案，可以选择的颜色为1到m

t=1

对当前第t个顶点开始着色：

 若t>n  则已求得一个解，输出着色方案即可

否则，依次对顶点t着色1-m，

   若t与所有其它相邻顶点无颜色冲突，则继续为下一顶点着色；否则，回溯，测试下一颜色。

   

//图着色问题回溯法
/*
无向图邻接矩阵示例
0 1 1 0 0
0 1 1 0 1
1 1 0 0 1
0 1 0 0 1
0 1 1 1 0
*/
#include<stdio.h>

int color[100];
//int c[100][100];
bool ok(int k ,int c[][100])//判断顶点k的着色是否发生冲突
{
    int i,j;
    for(i=1;i<k;i++)
        if(c[k][i]==1&&color[i]==color[k])
            return false;
        return true;
}

void graphcolor(int n,int m,int c[][100])
{
    int i,k;
    for(i=1;i<=n;i++)
        color[i]=0;//初始化
    k=1;
    while(k>=1)
    {
        color[k]=color[k]+1;
        while(color[k]<=m)
            if (ok(k,c)) break;
            else color[k]=color[k]+1;//搜索下一个颜色

        if(color[k]<=m&&k==n)//求解完毕，输出解
            {
                for(i=1;i<=n;i++)
                    printf("%d ",color[i]);
                printf("\n");
                //return;//return表示之求解其中一种解
            }
            else if(color[k]<=m&&k<n)
                k=k+1;    //处理下一个顶点
            else
            {
                color[k]=0;
                k=k-1;//回溯
            }
    }
}


void main()
{
    int i,j,n,m;
    int c[100][100];//存储n个顶点的无向图的数组
    printf("输入顶点数n和着色数m:\n");
    scanf("%d %d",&n,&m);
    printf("输入无向图的邻接矩阵:\n");
    for(i=1;i<=n;i++)
        for(j=1;j<=n;j++)
            scanf("%d",&c[i][j]);
    printf("着色所有可能的解:\n");
    graphcolor(n,m,c);
}