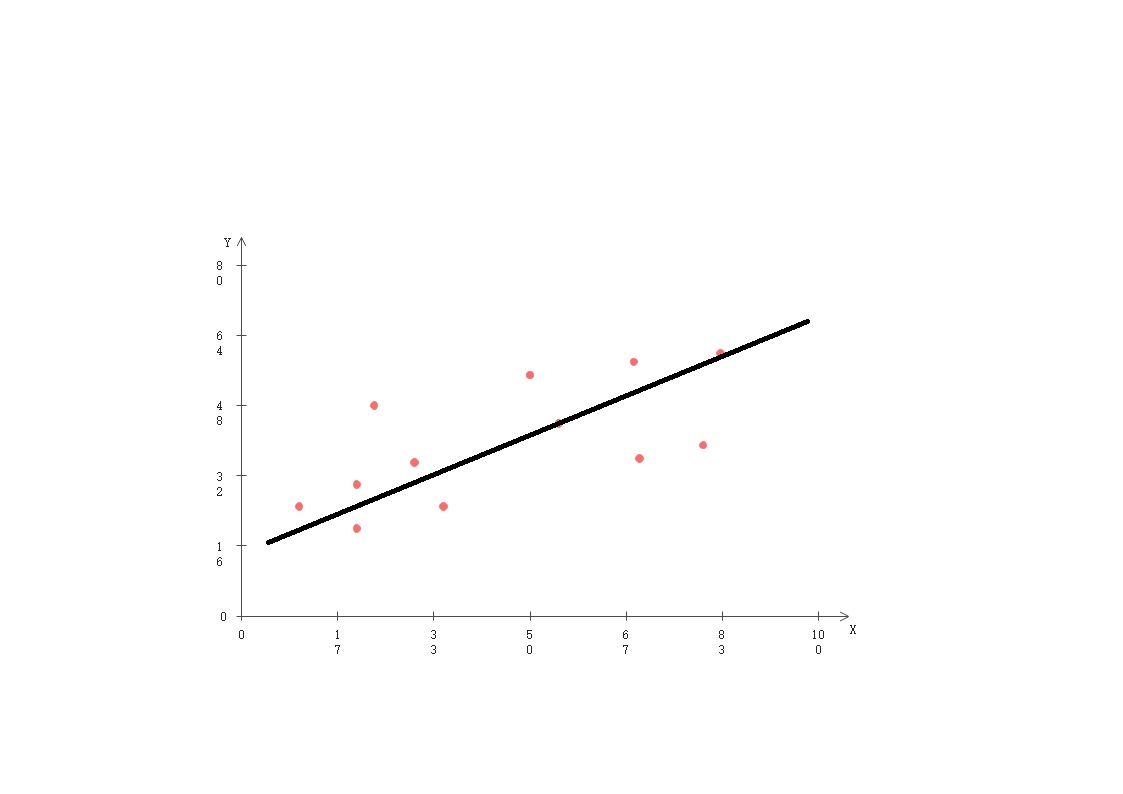
Training Set
训练集
| Size in feet2(x) | Price in 1000's(y) |
| 2104 | 460 |
| 1416 | 232 |
| 1534 | 315 |
| 852 | 178 |
Hypothesis:
[{h_ heta }left( x ight) = { heta _0} + heta {x}]
Notation:
θi's: Parameters
θi's: 参数
How to choose θi's?
如何选择θi's?

Idea: Choose θ0, θ1so that h(x) is close to y for our training examples(x, y)
思想:对于训练样本(x, y)来说,选择θ0,θ1 使h(x) 接近y。
minimize(θ0, θ1)[sumlimits_{i = 1}^m {{{left( {{h_ heta }left( {{x^{(i)}}} ight) - {y^i}} ight)}^2}} ]
选择合适的(θ0, θ1)使得 [sumlimits_{i = 1}^m {{{left( {{h_ heta }left( {{x^{(i)}}} ight) - {y^i}} ight)}^2}} ] 最小。
为了使公式的数学意义更好,将公式改为 [frac{1}{{2m}}sumlimits_{i = 1}^m {{{left( {{h_ heta }left( {{x^{(i)}}} ight) - {y^i}} ight)}^2}} ]
这并不影响 (θ0, θ1)的取值。
定义代价函数(Cost function) [Jleft( {{ heta _0},{ heta _1}} ight) = frac{1}{{2m}}sumlimits_{i = 1}^m {{{left( {{h_ heta }left( {{x^{(i)}}} ight) - {y^i}} ight)}^2}} ]
目标是 [mathop {min imize}limits_{{ heta _0},{ heta _1}} Jleft( {{ heta _0},{ heta _1}} ight)]
这个代价函数也称为平方误差代价函数(Squared error function)
总结:
Hypothesis: [{h_ heta }left( x ight) = { heta _0} + heta {x}]
Parameters: (θ0, θ1)
Cost Functions: [Jleft( {{ heta _0},{ heta _1}} ight) = frac{1}{{2m}}sumlimits_{i = 1}^m {{{left( {{h_ heta }left( {{x^{(i)}}} ight) - {y^i}} ight)}^2}} ]
Goal: [mathop {min imize}limits_{{ heta _0},{ heta _1}} Jleft( {{ heta _0},{ heta _1}} ight)]
例子帮助理解
首先令 θ0=0,则代价函数变为 [Jleft( {{ heta _1}} ight) = frac{1}{{2m}}sumlimits_{i = 1}^m {{{left( {{h_ heta }left( {{x^{(i)}}} ight) - {y^i}} ight)}^2}} ]
| hθ(x) | J(θ1) |
| 对于给定θ1的情况,它是x的函数 | 是θ1的函数 |
三个训练样本
| x | y |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
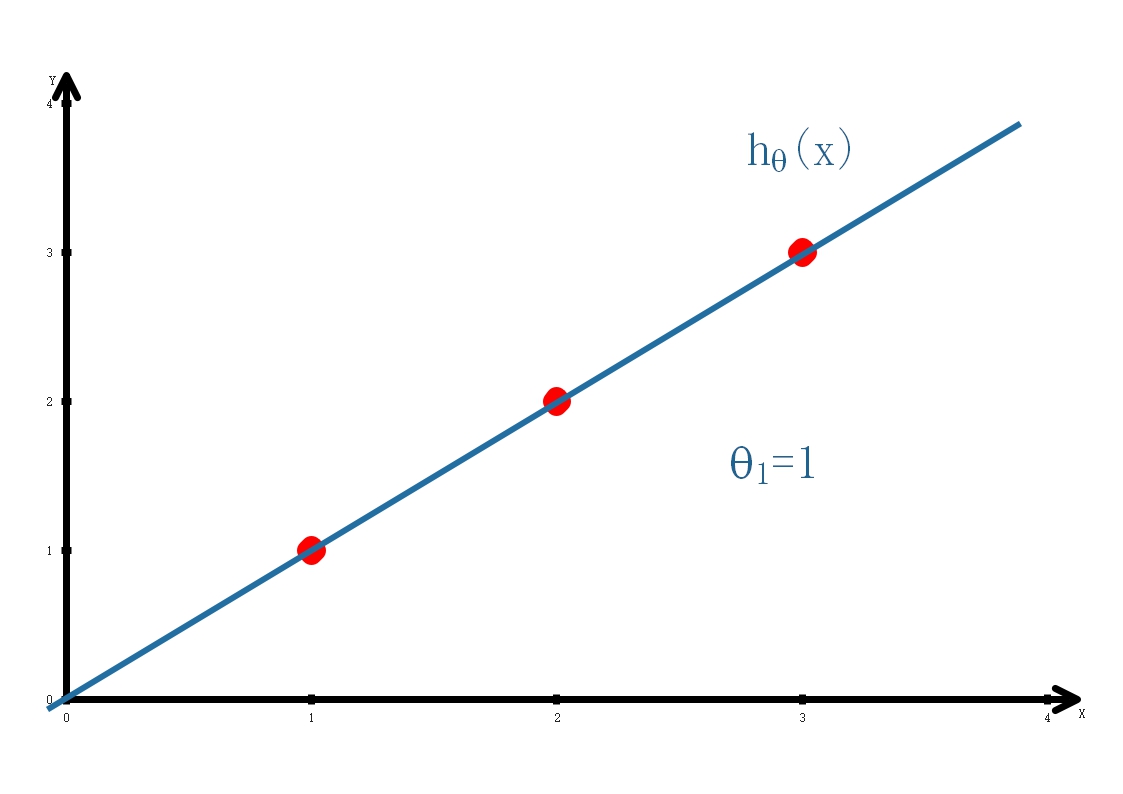
当θ1=1时,[Jleft( {{ heta _1}} ight) = frac{1}{{2m}}left( {{0^2} + {0^2} + {0^2}} ight) = 0]
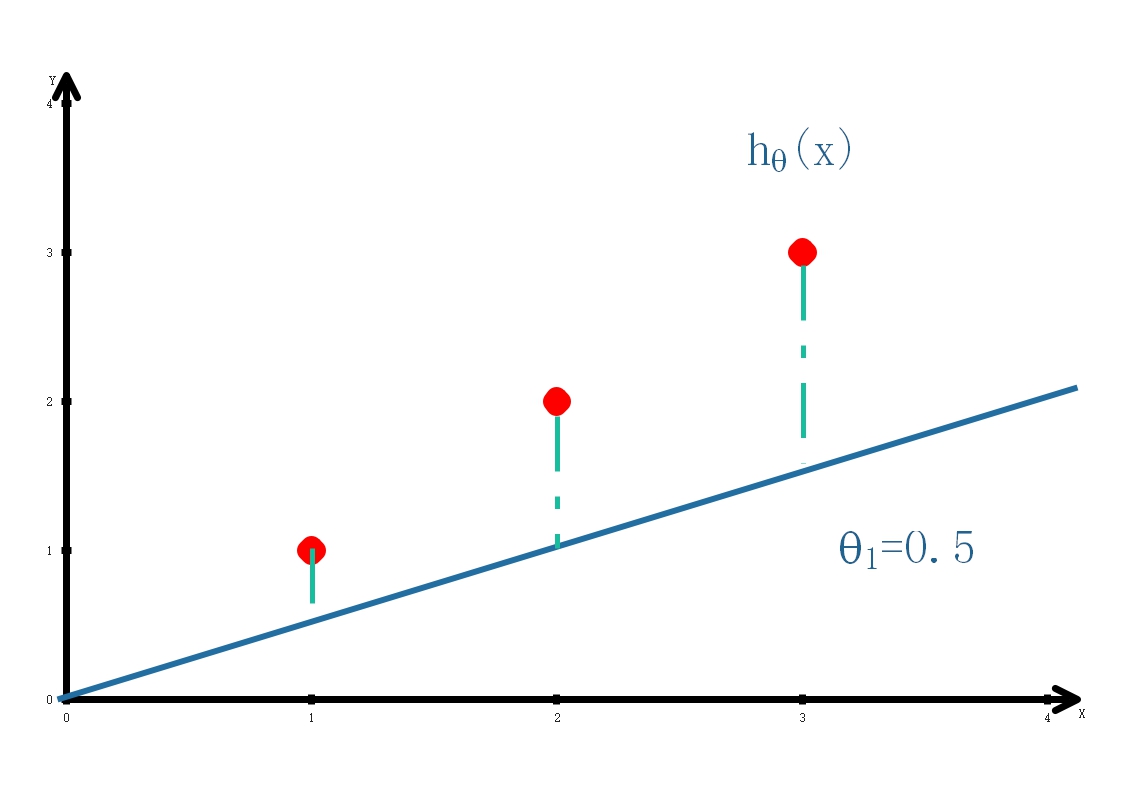
当θ1=0.5时,[Jleft( {0.5} ight) = frac{1}{{2*3}}left( {{{left( {0.5 - 1} ight)}^2} + {{left( {{ m{1 - 2}}} ight)}^2} + {{left( {{ m{1}}{ m{.5 - 3}}} ight)}^2}} ight) approx { m{0}}{ m{.58}}]

θ1取不同值J(θ1)的值
每一个不同θ1的对应一条直线,我们的目的是找出最合适的θ1(最适合的直线)
如果同时考虑θ0, θ1,那么代价函数J(θ0, θ1)的值可能会是下图所示
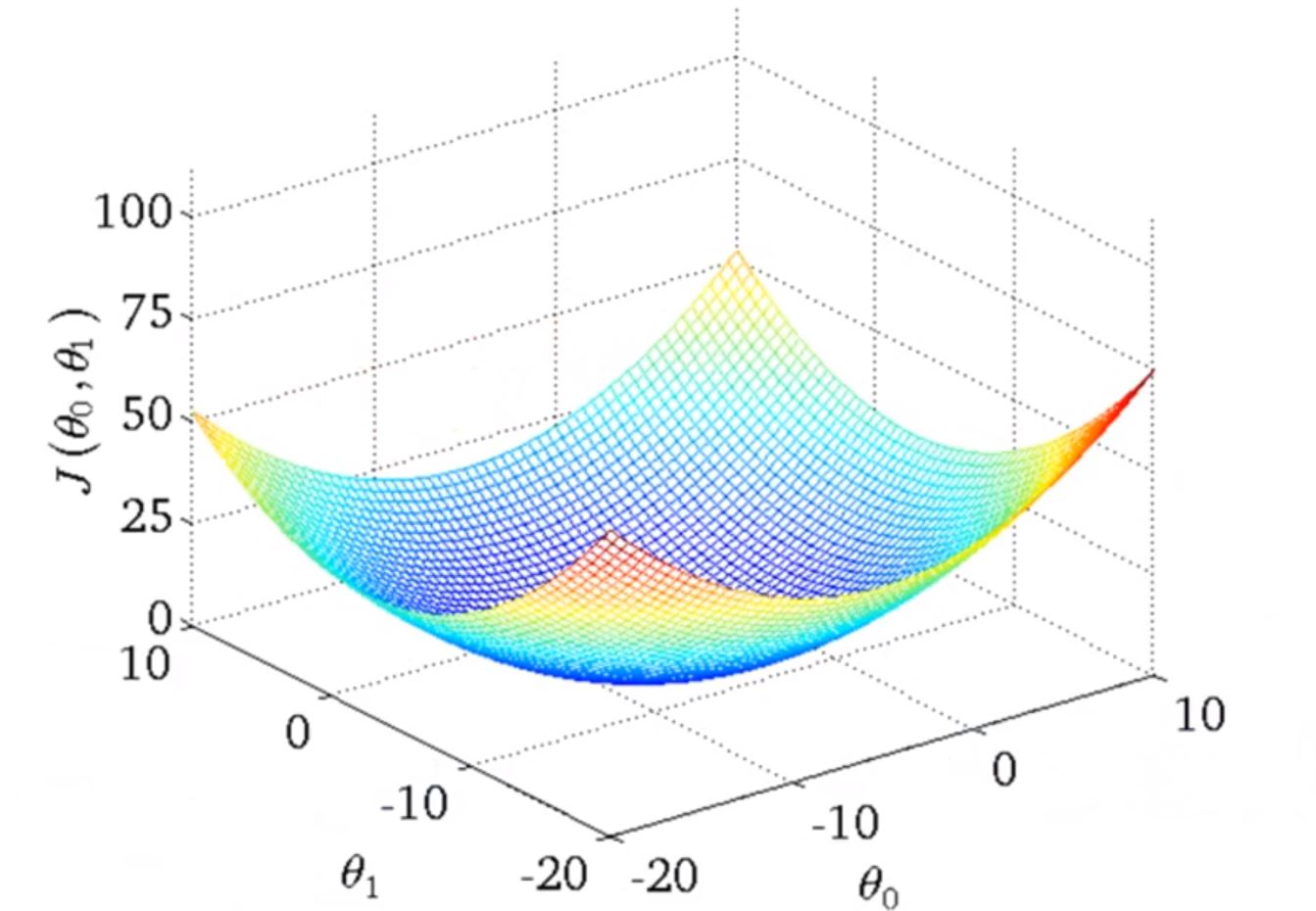
为了方便,使用等高线代表这种图
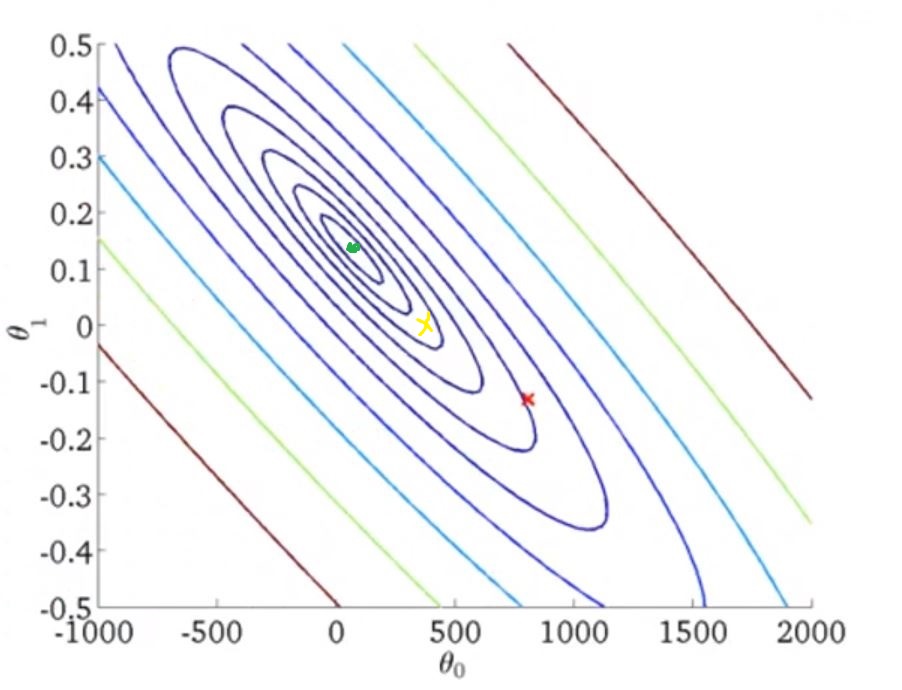
对于不同的(θ0, θ1)组合,如果它们在同一个圆圈上,它们就有相同的J(θ0, θ1)。
此时最小的J(θ0, θ1)在绿点位置。
对比J(θ0, θ1)和h(x)更好理解
当(θ0, θ1)选为红点位置时,h(x)可能是下图所示
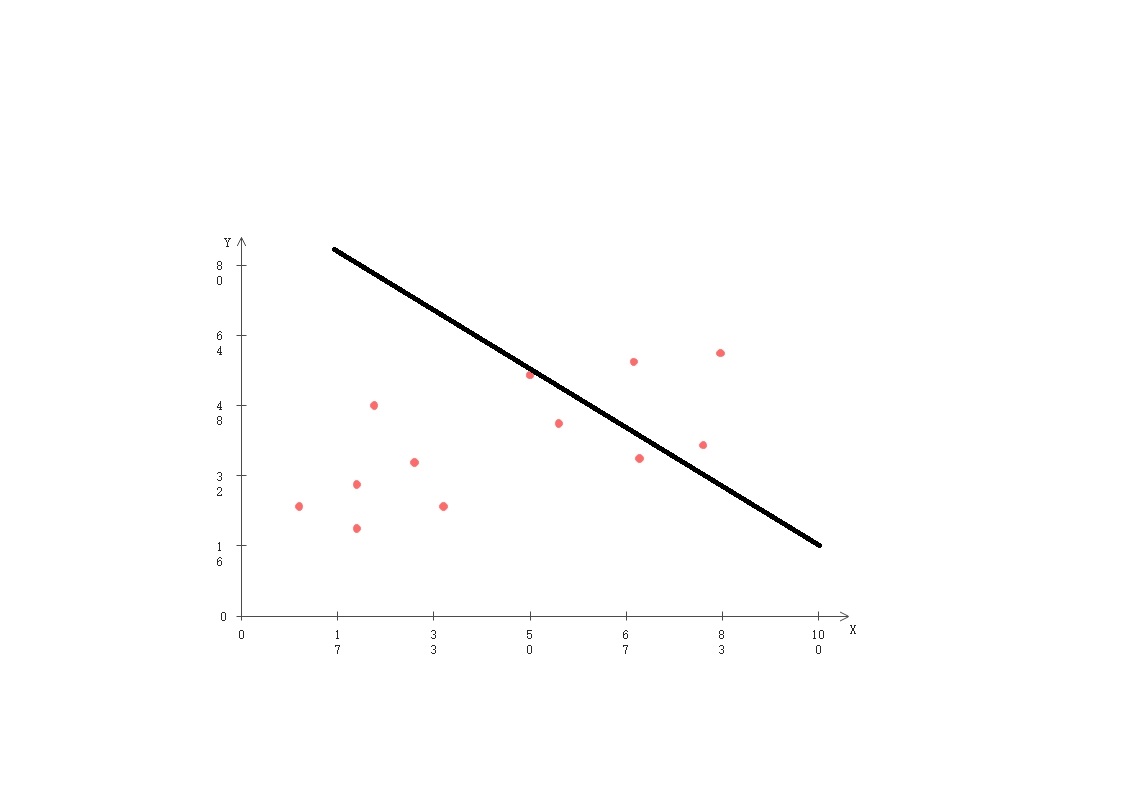
当(θ0, θ1)选为黄点位置时,h(x)可能是下图所示
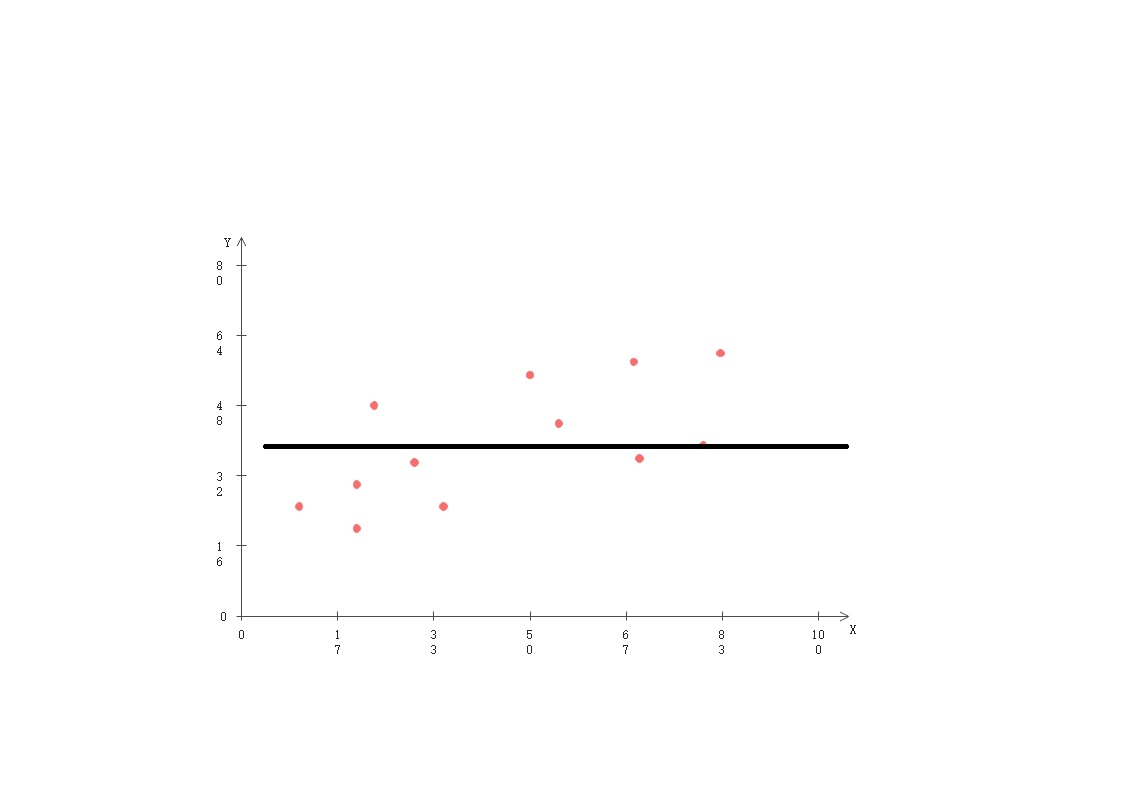
当(θ0, θ1)选为绿点位置时,h(x)可能是下图所示