覆盖墙壁

【题目描述】

你有一个长为N宽为2的墙壁，给你两种转头：一个长2宽1，另一个是L型覆盖3个单元的转头。如下图：

 

 

转头可以旋转，两种转头可以无限制提供。你的任务是计算用这两种来覆盖N*2的墙壁的覆盖方法。例如一个2*3的墙可以有5种覆盖方法，如下：

 

注意可以使用两种转头混合起来覆盖，如2*4的墙可以这样覆盖：

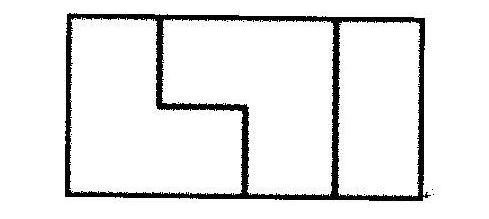
给定N，要求计算2*N的墙壁的覆盖方法。由于结果很大，所以只要求出输出最后4位。例如2*13的覆盖方法为13465，只需输出3465即可。如果答案少于4位，就直接输出就可以，不用加0，如N=3时输出5.                

【输入格式】

一个整数N（1<=n<=1000000），表示墙壁的长。

【输出格式】

输出覆盖方法的最后4位，如果不足4位就输出整个答案。

【样例输入】

13

【样例输出】

3465

---

 思路：

定义f[1000001][3] 

表示当前排到了第0..1000000列格子，连接处状态为0..3的排列方法数。

定义

f[i][0]为第i列两格都没放了的状态

f[i][1]为第i列上面那格放了的状态

f[i][2]为第i列下面那格放了的状态

f[i][3]为第i列两格都放了的状态

初始化

f[1][0]=1;f[1][3]=1;

递推公式 //取模10000要注意

f[i][0]=f[i-1][3];

f[i][1]=(f[i-1][0]+f[i-1][2])%10000;

f[i][2]=(f[i-1][0]+f[i-1][1])%10000;

f[i][3]=(f[i-1][1]+f[i-1][2]+f[i-1][0]+f[i-1][3])%10000;

代码：

#include<stdio.h>
int len,f[1000001][4]; 

int main() 
{
//    freopen("wall.in","r",stdin),freopen("wall.out","w",stdout);
    scanf("%d",&len);
    f[1][0]=1,f[1][3]=1;
    for(int i=2;i<=len;++i) 
    {
        f[i][0]=f[i-1][3]%10000;
        f[i][1]=(f[i-1][0]+f[i-1][2])%10000;
        f[i][2]=(f[i-1][0]+f[i-1][1])%10000;
        f[i][3]=(f[i-1][0]+f[i-1][1]+f[i-1][2]+f[i-1][3])%10000;
    }
    printf("%d",f[len][3]);
    return 0;
}