字符串模式匹配有着广泛的应用,如求最大公共子串、最长回文字符串、L-Gap、数据压缩、DNA序列匹配等问题。所谓模式匹配就是在目标字符串中寻找第一个子串在目标串中的位置的过程,要寻找的字串即为模式。
模式 P :“jin”
匹配结果= 3
一、BF算法(也叫传统的字符串模式匹配算法、朴素模式匹配、穷举模式匹配)
BF(Bruce Force)算法是普通的模式匹配算法,BF算法的思想就是将目标串S的第一个字符与模式串P的第一个字符进行匹配,若相等,则继续比较S的第二个字符和P的第二个字符;若不相等,则比较S的第二个字符和P的第一个字符,依次比较下去,直到得出最后的匹配结果。(通俗的解释)
BF(Bruce Force)算法可以说是模式匹配算法中最简单、最容易理解的一个。原理很简单。其基本思想是从主串的start位置开始与模式串进行匹配,如果相等,则继续比较后续字符,如果不相等则模式串回溯到开始位置,主串回溯到start+1位置,继续进行比较直至模式串的所有字符都已比较成功则匹配成功,或者主串所有的字符已经比较完毕,没有找到完全匹配的字串,则匹配失败。(引用别人的解释)
1.1举例说明
S: ababcababa
P: ababa
BF算法匹配的步骤如下
i=0 i=1 i=2 i=3 i=4
第一趟:ababcababa 第二趟:ababcababa 第三趟:ababcababa 第四趟:ababcababa 第五趟:ababcababa
ababa ababa ababa ababa ababa
j=0 j=1 j=2 j=3 j=4(i和j回溯)
i=1 i=2 i=3 i=4 i=3
第六趟:ababcababa 第七趟:ababcababa 第八趟:ababcababa 第九趟:ababcababa 第十趟:ababcababa
ababa ababa ababa ababa ababa
j=0 j=0 j=1 j=2(i和j回溯) j=0
i=4 i=5 i=6 i=7 i=8
第十一趟:ababcababa 第十二趟:ababcababa 第十三趟:ababcababa 第十四趟:ababcababa 第十五趟:ababcababa
ababa ababa ababa ababa ababa
j=0 j=0 j=1 j=2 j=3
i=9
第十六趟:ababcababa
ababa
j=4(匹配成功)
1.2参考别人的C代码实现
public class BR_String {
/**
*
* @param s
* 主串
* @param p
* 模式串
* @return 模式串在主串中第一次出现的位置,如果找不到则返回-1
*/
static int BF(String s, String p) {
int i = 0, j = 0;
while (i < s.length())
{
j = 0;
while (j < p.length() && s.charAt(i) == p.charAt(j)) // 如果相等,则继续比较后续字符
{
i++;
j++;
}
if (j == p.length())
return i - p.length();
i = i - j + 1; // 指针i回溯
}
return -1;
}
public static void main(String[] args) {
String s = "ababcababa";
String p = "ababa";
System.out.println(s.indexOf(p));// 用来验证的
System.out.println(BF(s, p));
}
}
1.3、第一次看完BF算法的定义以后自己写的代码
以下代码是第一次看完BF算法的定义以后自己写的。和上面基本相同,可能理解起来简单点。(以主串为参照,主串的第i个字符和模式串的第一个字符比较,第[i+j]个字符和模式串的第j个字符比较,s[i+j] 和p[j]不相等时候,j变成0,i++,相当于回溯了)
public class BR_String {
/**
*
* @param s
* 主串
* @param p
* 模式串
* @return 模式串在主串中第一次出现的位置,如果找不到则返回-1
*/
static int BF(String s, String p) {
int m = s.length() - p.length(); //
int n = p.length();
int index = 0; // 记录位置,以便成功时返回字串在主串的位置
int start = 0;// start为从第start位置的字符开始比较
while (start < n && index <= m) {
if (s.charAt(index + start) == p.charAt(start))
// 如果相等,则继续比较后续字符
start++;
else {
// 如果不相等则模式串回溯到开始位置,主串回溯到start+1位置,继续进行比较;
index++;
start = 0;
}
}
if (start == p.length()) {
return index;
}
return -1;
}
public static void main(String[] args) {
String s = "ababcababa";
String p = "ababa";
System.out.println(BF(s, p));
System.out.println(s.indexOf(p));// 用来验证的
}
}
其实在上面的匹配过程中,有很多比较是多余的。在第五趟匹配失败的时候,在第六趟,i可以保持不变,j值为2。因为在前面匹配的过程中,对于串S,已知s0s1s2s3=p0p1p2p3,又因为p0!=p1!,所以第六趟的匹配是多余的。又由于p0==p2,p1==p3,所以第七趟和第八趟的匹配也是多余的。在KMP算法中就省略了这些多余的匹配。
二、KMP算法
一种由Knuth(D.E.Knuth)、Morris(J.H.Morris)和Pratt(V.R.Pratt)三人设计的线性时间字符串匹配算法,就取三个人名字的首字母作为该算法的名字。可使目标串的检测指针每趟不回退。其实KMP算法与BF算法的区别就在于KMP算法巧妙的消除了指针i的回溯问题,只需确定下次匹配j的位置即可,使得问题的复杂度由O(mn)下降到O(m+n)。
在KMP算法中,为了确定在匹配不成功时,下次匹配时j的位置,引入了next[]数组,next[j]的值表示P[0...j-1]中最长后缀的长度等于相同字符序列的前缀。
1、失效函数
定义:若设模式 P =p0p1…pm-2pm-1
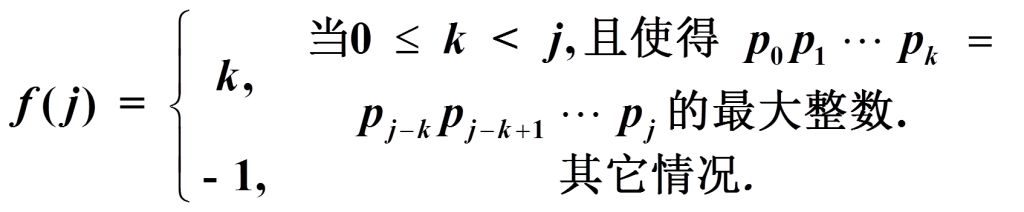
示例:确定失效函数f(j)

2、利用失效函数 f (j)的匹配处理
如果 j =0,则目标指针加 1,模式指针回到p0。
如果 j >0,则目标指针不变,模式指针回到pf(j-1)+1。
public static int KMPMatch(String s, String p) {
int next[] = getNext(p);
int i = 0, j = 0;
while (i < s.length())
{
if ((s.charAt(i) == p.charAt(j))) { // 匹配的时候 ,目标串和模式串的指针都后移
i++;
j++;
}
else if (j == 0) // 不匹配,如果 j=0,相当于和模式串的第0个字符不相等,则目标指针加
// 1,继续和模式串的第0个字符比较。
i++;
else
j = next[j - 1] + 1; // 不匹配,如果 j>0,则目标指针不变,模式指针回到 next(j-1)+1。
if (j == p.length())
return i - p.length();
}
return -1;
}
3、失效函数的求法
1、第一种思路是用递推的思想去求算

public static int[] getNext(String p) {
int next[] = new int[p.length()];
next[0] = -1;
for (int j = 1; j < p.length(); j++) {
int i = next[j - 1];
while (p.charAt(i + 1) != p.charAt(j) && i >= 0) //这里搞不明白
i = next[i];
if (p.charAt(i + 1) == p.charAt(j))
next[j] = i + 1;
else
next[j] = -1;
}
return next;
}
2、根据定义直接求解
public static int[] getNext_by_Definition(String p) {
int next[] = new int[p.length()];
next[0] = -1;
for (int j = 1; j < p.length(); j++) {
int i = j;
while (i <= j && i > 0) {
if (p.substring(0, i).equals(p.substring(j - i + 1, j + 1)))
{
next[j] = i - 1;
break;
}
else {
i--;
}
if (i == 0)
next[j] = -1;
}
}
return next;
}
