前几天做了6050原始数据的串口输出和上位机波形的查看。这篇博客我们来看一下对原始数据的处理。
任务:利用STC89C52RC对MPU6050原始数据进行滤波与姿态融合。
首先我摘抄了一段别人在昨晚这个实验的写的最后总结。
1.尽量不要用MPU6050内置的LPF滤波。虽然相比于原始加速度计输出,该LPF可以平滑输出,但是在FFT频谱上的表现相当差劲。
2.广泛使用的窗口平均滑动滤波无论在FFT还是RMSE表现上都有不错的表现,所以一般基础应用(低速运动或四轴初学者)采用窗口平均滤波是比较明智的选择。
3.想要达到更好的滤波效果,FIR或者IIR滤波器是更好的选择。笔者测试2阶30Hz的Butterworth滤波器虽然在平滑性RMSE只比窗口平均滑动差了一点(但是比LPF要好),但是数据实时性性能指标上比前者响应速度提高了近一倍。因此在制作四轴的进阶阶段,可以考虑将窗口平均滑动换成Butterworth滤波器。
开发日记,不想看的可以跳过,仅仅是为了记录自己的过程。
//----------------------------------------------------------------------------------------------------------------------------------------
2017.12.5 晚
刚刚写完6050的零偏矫正和滑动窗口滤波,就已经超过51单片机内部最大RAM允许范围了。具体表现为:
USERSMPU6050.C(241): error C249: 'DATA': SEGMENT TOO LARGE
定义的数据段大于单片机内部RAM,
查了资料,原来这段程序并没有把stc89c52内部的512字节的RAM全部用完!而是用完了开头的128字节的数据(0X00-0X7F)后面还有128*3的字节量没有被使用。
另外,当我们程序中总变量的字节数超过128字节时,必须对程序中所有变量进行初始化,否则没有被初始化的变量默认值不在是0,而是不确定的随机数。这时我们必须在keil中设置存储器的存储模式。但是当你的变量总字节在128字节以内的话,并且存储模式为small模式时,没有初始化的变量的默认值才是0.
1.Small模式
所有缺省变量参数均装入内部 128字节 RAM,优点是访问速度快,缺点是空间有限,只适用于小程序。
2. Compact 模式
所有缺省变量均位于外部RAM区的一页(256Byte)。和small模式中使用pdata定义变量的效果相同。如:uchar pdata a[100]; 该模式下,总变量不得超过256字节。
3. Large 模式
所有缺省变量可放在多达 64KB 的外部RAM 区,优点是空间大,可存变量多,缺点是速度较慢。在large模式下,和在small模式中使用关键字xdata 定义变量的效果一样。如:char xdata a[100];这样显式的规定了变量的存放区域,以定义为准,不受存储模式的影响。在此模式下编写程序时,定义的变量不要超过单片机规定的内部最大RAM数,因为即使超过了,编译器也不会报错,但是程序运行一定出错。
注意: 为了程序安全,当程序中定义超过128字节的数据时,最好申明为xdata
型,为其在扩展RAM中分配内存。
2017.12.6 下午
一般我们最好配置为small模式,然后必要的情况下,使用xdata对变量进行说明。
/************
注意看编译后的这个,他们的单位时字节B。而1k = 1024B
Program Size: data=16.1 xdata=247 code=3424
/************
由于在6050数据处理函数中多次使用静态局部变量,所以加深一下对他的理解。
对静态局部变量的说明:
(1) 静态局部变量在静态存储区内分配存储单元。在程序整个运行期间都不释放。而自动变量(即动态局部变量)属于动态存储类别,存储在动态存储区空间(而不是静态存储区空间),函数调用结束后即释放。
(2) 为静态局部变量赋初值是在编译时进行值的,即只赋初值一次,在程序运行时它已有初值。以后每次调用函数时不再重新赋初值而只是保留上次函数调用结束时的值。而为自动变量赋初值,不是在编译时进行的,而是在函数调用时进行,每调用一次函数重新给一次初值,相当于执行一次赋值语句。
(3) 如果在定义局部变量时不赋初值的话,对静态局部变量来说,编译时自动赋初值0(对数值型变量)或空字符(对字符型变量)。而对自动变量来说,如果不赋初值,则它的值是一个不确定的值。这是由于每次函数调用结束后存储单元已释放,下次调用时又重新另分配存储单元,而所分配的单元中的值是不确定的。
(4) 虽然静态局部变量在函数调用结束后仍然存在,但其他函数是不能引用它的,也就是说,在其他函数中它是“不可见”的。
不管怎么修改量程,输出的波形震动范围总是在+-20000波动,但是当我把加速度计的量程设置为+-16G的时候,理论上其LSB应该为2048左右,但是发现输出的波形也是震动范围很大。而且陀螺仪的数据比一开始不处理的时候震动更加明显。
内存覆盖:
以覆盖的(某个函数的局部变量空间在退出该函数是就释放,由别的函数的局部变量覆盖),可以提高内存利用率。当然静态局部变量除外,其内存使用方式与全局变量相同;
2017.12.7 晚
今天发现我的程序确实存在问题,就是运算时的数据溢出。在进行零偏数据的计算时,需要将200个原始数据相加,但是一开始我的总和定义的还是一个int型的数据,这时200个数据的和可能已经超过了int型数据的取值范围,所以产生了溢出。导致数据的不准确。那么后面计算的数据也是不准确的。所以我晃动传感器曲线都没有什么变化。唉,学单片机都得过数据类型、内存管理这道坎啊。
2017.12.11 下午
如果全是自己开发的话,没有人指导的情况下,每一个小小的进步,都是非常不容易的!!
2017.12.12 晚
目前的问题就是静止状态下陀螺仪输出的数据不为零。还有就是由于单片机运算能力的限制,输出的波形延迟较大。
//---------------------------------------------------------------------------------------------------------------
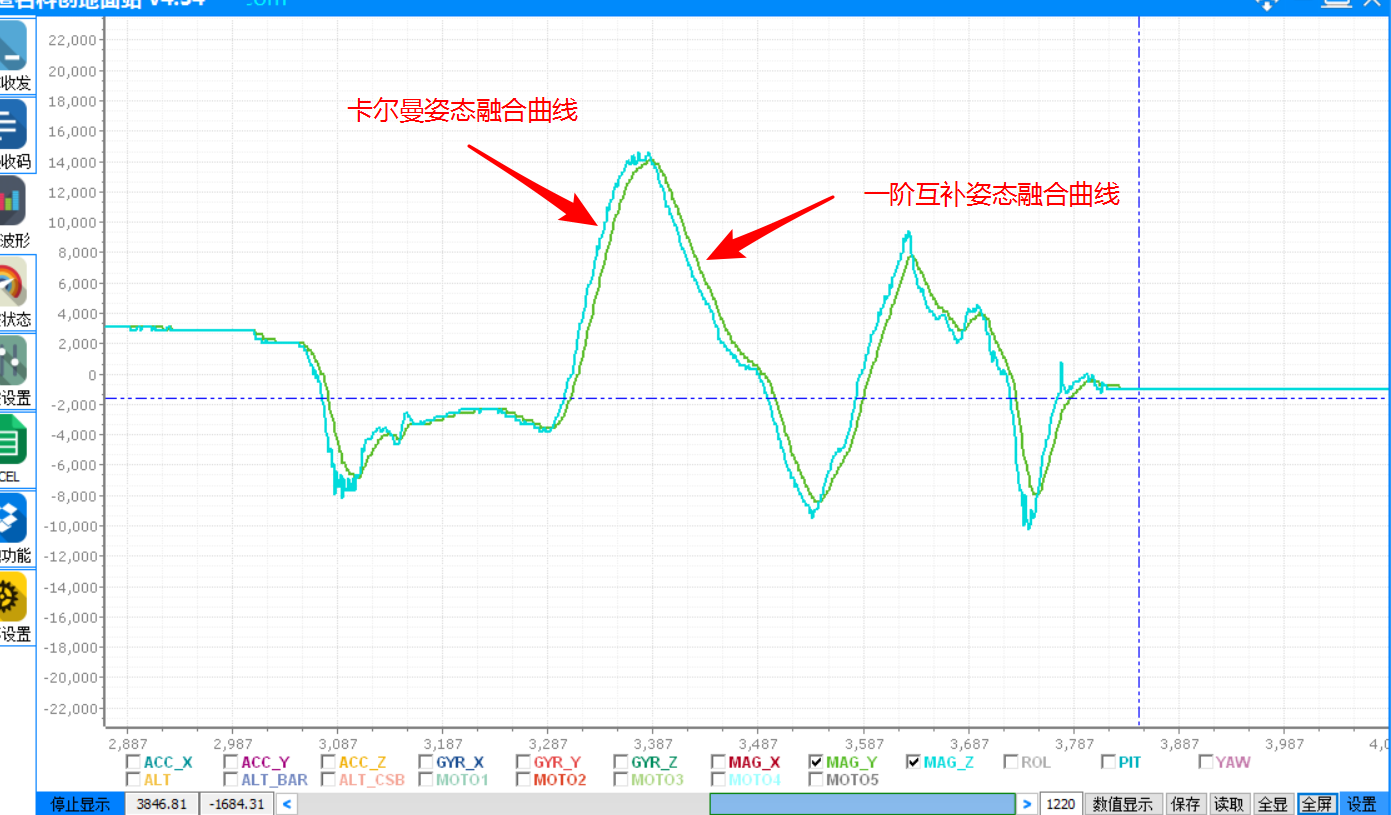
经过大概一个星期的尝试,终于用51单片机对6050进行了正确的读取与姿态融合。其实现在想想自己这几天所做的所有事情,并不多。程序前两天就写完了,后面的大部分时间都是在对程序进行调整,对波形进行分析。从刚开始凌乱的波形,到后面使用一阶互补滤波和卡尔曼滤波得出一个姿态角的流畅波形。这中间的苦恼和困难只有自己知道。也行对于一个老手来说,我这几天所做的所有事情,他能在一上午或者几个小时内完成,但是这几天所有的思考与疑惑都对我有很大的帮助。慢慢的养成了分析思考问题的方法。遇到问题不要慌张,一点点的去分析。不要放过任何一个细节。其实我们常说,一个经验丰富的老手能很快的解决一个棘手的问题。他们靠的是什么?所有人都知道是经验。但是经验又是什么?说的通俗一点,经验就是他们所有踩过的坑,进行过的所有思考。
想说一个我在做这个实验小小的插曲,有一天的时间,波形出来的都是方波,稍微动一下就满量程,波形很难看。想了很久,检查了不知多少遍代码,逻辑没问题啊,也没有报错,怎么波形就不对呢?突然一瞬间,发现了一点小问题。一个计数变量,定义了一个unsigned char i;来进行零偏数据的计数,每500个数据进行一次平均,刚开始愣是没发现不对。unsigned char 变量的最大计数是256!!!
一个计数变量 ,平时根本就不会去注意他的,但是关键时候就是他搅的局。改了这个错误之后,波形看起来好了很多。
首先在上次博客的基础上,先进行一次滑动平均滤波,滤波窗口大致为6个数据。
/* **2017.12.5 **对6050的原始数据进行处理,滤波,角度转换。 **滑动平均滤波 */ void mpu6050_data_process(void) { unsigned char i = 0, j = 0; static unsigned char acc_filter_cnt = 0;//滤波次数计数 static unsigned char gyro_filter_cnt = 0; long int xdata acc_temp[3] = {0};//三轴加速度,注意,这个不能定义为静态 long int xdata gyro_temp[3] = {0}; static int acc_x_buf[ACC_FILTER_NUM] = {0}, //滑动窗口缓存,每调用一次,里面数据多一个。 acc_y_buf[ACC_FILTER_NUM] = {0}, acc_z_buf[ACC_FILTER_NUM] = {0}; static int gyro_x_buf[GYRO_FILTER_NUM] = {0}, //滑动窗口缓存,每调用一次,里面数据多一个。 gyro_y_buf[GYRO_FILTER_NUM] = {0}, gyro_z_buf[GYRO_FILTER_NUM] = {0}; float xdata init_ax = 0,init_ay = 0,init_az = 0; float xdata acc_angle_x = 0,gyro_angle_x = 0; //一阶互补的参数传递 mpu6050_read_acc(); //获取原始数据 mpu6050_read_gyro(); init_ax = (float)mpu_data.acc_data.x / ACC_G; //计算单位为G的各轴重力加速度分量 init_ay = (float)mpu_data.acc_data.y / ACC_G; init_az = (float)mpu_data.acc_data.z / ACC_G; acc_angle_x = atan(init_ax/init_az) * 180 / PI ; //加速度计x轴角度 gyro_angle_x = -(float)mpu_data.gyro_data.y / 7510.0; //陀螺仪计算x轴角度,7150?? mpu_data.acc_angle.x = (int)one_filter(acc_angle_x,gyro_angle_x); //一阶互补滤波,获取偏x轴角度 mpu_data.acc_angle.y = (int)kalman_filter(acc_angle_x,gyro_angle_x); //获取卡尔曼滤波 //加速度计数据处理 //----------------------------------------------------- acc_x_buf[acc_filter_cnt] = mpu_data.acc_data.x;//平均滤波 ,更新数据,一开始这里写成了加,数据一直不对 acc_y_buf[acc_filter_cnt] = mpu_data.acc_data.y; acc_z_buf[acc_filter_cnt] = mpu_data.acc_data.z; for(i=0;i<ACC_FILTER_NUM;i++) //滑动滤波,取平均值 { acc_temp[0]+= acc_x_buf[i]; acc_temp[1]+= acc_y_buf[i]; acc_temp[2]+= acc_z_buf[i]; } //在此进行 六面校准 //--------------------------- mpu_data.acc_filter.x = (acc_temp[0] / ACC_FILTER_NUM); //得出沿x轴方向的重力加速度, 单位G mpu_data.acc_filter.y = (acc_temp[1] / ACC_FILTER_NUM); mpu_data.acc_filter.z = (acc_temp[2] / ACC_FILTER_NUM); //-------------------------- acc_filter_cnt++; if(acc_filter_cnt == ACC_FILTER_NUM) { acc_filter_cnt = 0; } //陀螺仪数据处理 //----------------------------------------------------------- gyro_x_buf[gyro_filter_cnt] = mpu_data.gyro_data.x; gyro_y_buf[gyro_filter_cnt] = mpu_data.gyro_data.y; gyro_z_buf[gyro_filter_cnt] = mpu_data.gyro_data.z; for(j=0;j<GYRO_FILTER_NUM;j++) //滑动滤波,取平均值 { gyro_temp[0]+= gyro_x_buf[j]; gyro_temp[1]+= gyro_y_buf[j]; gyro_temp[2]+= gyro_z_buf[j]; } //在此进行 六面校准 //----------------------------- mpu_data.gyro_filter.x = gyro_temp[0]/GYRO_FILTER_NUM; mpu_data.gyro_filter.y = gyro_temp[1]/GYRO_FILTER_NUM; mpu_data.gyro_filter.z = gyro_temp[2]/GYRO_FILTER_NUM; //-------------------------- gyro_filter_cnt++; if(gyro_filter_cnt == GYRO_FILTER_NUM) { gyro_filter_cnt = 0; } //化为度制 // mpu_data.gyro_dps.x = (float)mpu_data.gyro_filter.x * GYRO_A; // mpu_data.gyro_dps.y = (float)mpu_data.gyro_filter.y * GYRO_A; // mpu_data.gyro_dps.z = (float)mpu_data.gyro_filter.z * GYRO_A; // // //化为弧度制 // mpu_data.gyro_rad.x = (float)mpu_data.gyro_filter.x * GYRO_R; // mpu_data.gyro_rad.y = (float)mpu_data.gyro_filter.y * GYRO_R; // mpu_data.gyro_rad.z = (float)mpu_data.gyro_filter.z * GYRO_R; }
数据波形为:
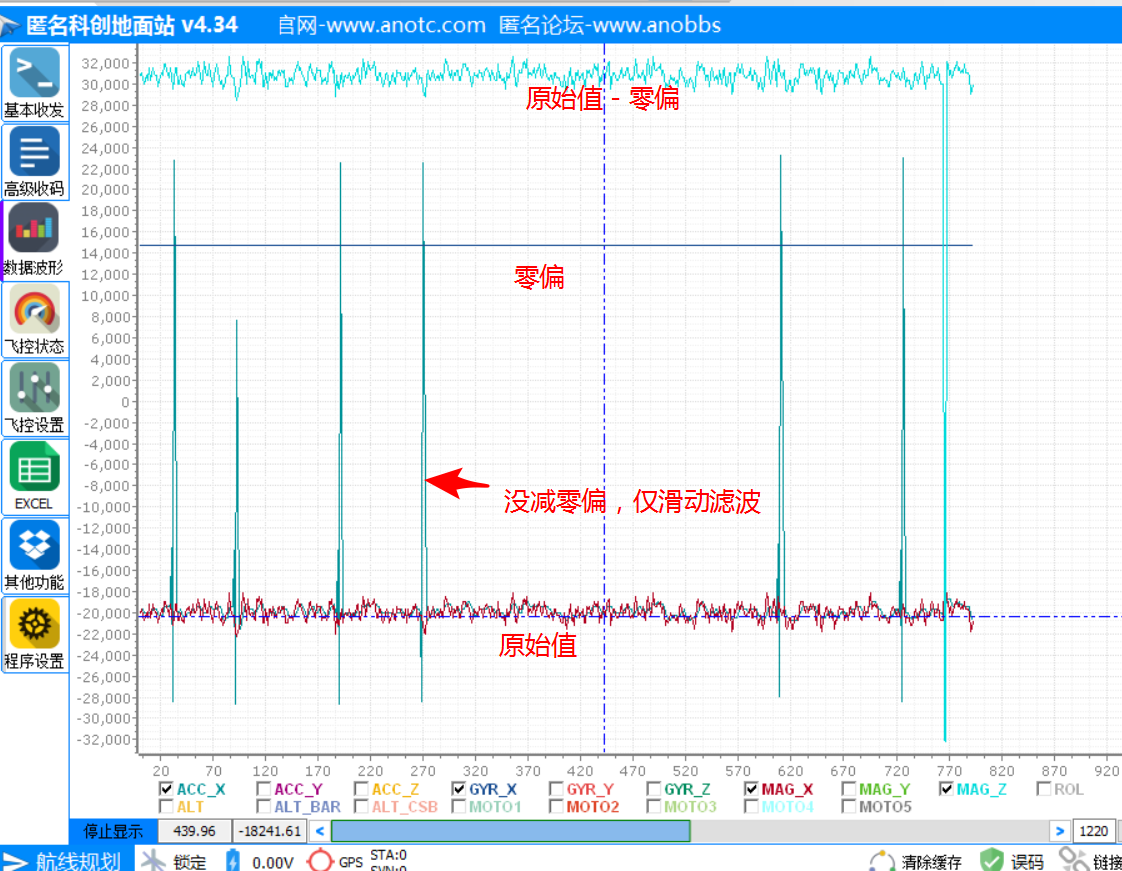
这些仅仅是对原始数据的滤波处理,因为加速度计包含了太多的噪声。陀螺仪一般不需要滤波,原始值就很稳定,就是陀螺仪刚开始可能会有零偏,需要我们手动减去这个值。MPU6050 可以输出三轴的加速度和角速度。通过加速度和角速度都可以得到 Pitch 和 Roll 角(加速度不能得到 Yaw 角),就是说有两组 Pitch、Roll 角,到底应该选哪组呢?别急,先分析一下。MPU6050 的加速度计和陀螺仪各有优缺点,三轴的加速度值没有累积误差,且通过算 tan() 可以得到倾角,但是它包含的噪声太多(因为待测物运动时会产生加速度,电机运行时振动会产生加速度等),不能直接使用;陀螺仪对外界振动影响小,精度高,通过对角速度积分可以得到倾角,但是会产生累积误差。所以,不能单独使用 MPU6050 的加速度计或陀螺仪来得到倾角,需要互补。一阶互补算法的思想就是给加速度和陀螺仪不同的权值,把它们结合到一起,进行修正。
然后就可以利用这个加速度计和陀螺仪的数据进行姿态融合。姿态融合一方面对数据进行了滤波,一方面计算出了角度值。所以也可以利用原始数据进行姿态融合。因为我使用的是51系列的单片机,运算速率很慢,在此我直接用原始数据除精度后进行一阶互补滤波,得出了x轴的偏移角度。然后再用卡尔曼滤波对姿态进行融合,对比两种融合方式的波形。
loat xdata one_filter_angle = 0; float xdata kalman_filter_angle = 0, kalman_filter_angle_dot = 0; //---------------- //在进行滤波之前,需要获取原始数据 float one_filter(float angle_m,float gyro_m) { float xdata K1 =0.1; // 对加速度计取值的权重 float xdata dt=0.005;//注意:dt的取值为滤波器采样时间 one_filter_angle = K1 * angle_m+ (1-K1) * (one_filter_angle + gyro_m * dt); return one_filter_angle; } //------------------ float kalman_filter(float angle_m,float gyro_m) { //滤波参数 float xdata dt = 0.005; //卡尔曼采样时间 float xdata P[2][2] = {{1,0},{0,1}}; float xdata Pdot[4] = {0,0,0,0}; float xdata Q_angle = 0.001;//角度数据置信度,陀螺仪协方差 float xdata Q_gyro = 0.005; //角速度数据置信度,陀螺仪飘移噪声协方差 float xdata R_angle = 0.5; //加速度计协方差 char xdata C_0 = 1; float xdata q_bias = 0,angle_err = 0; //q_bias为陀螺仪飘移 float xdata PCt_0 = 0,PCt_1 = 0,E = 0; float xdata K_0 = 0, K_1 = 0, t_0 = 0, t_1 = 0; kalman_filter_angle+= (gyro_m - q_bias) * dt; //卡尔曼预测方程,认为每次飘移相同, Pdot[0]=Q_angle - P[0][1] - P[1][0]; Pdot[1]=- P[1][1]; Pdot[2]=- P[1][1]; Pdot[3]=Q_gyro; P[0][0] += Pdot[0] * dt; P[0][1] += Pdot[1] * dt; P[1][0] += Pdot[2] * dt; P[1][1] += Pdot[3] * dt; PCt_0 = C_0 * P[0][0]; //矩阵乘法中间变量 PCt_1 = C_0 * P[1][0]; E = R_angle + C_0 * PCt_0; //分母 K_0 = PCt_0 / E; //增益值 K_1 = PCt_1 / E; angle_err = angle_m - kalman_filter_angle; kalman_filter_angle += K_0 * angle_err; //对状态的卡尔曼估计,最优角度 q_bias += K_1 * angle_err; kalman_filter_angle_dot = gyro_m-q_bias;//最优角速度 t_0 = PCt_0; //矩阵计算中间变量 t_1 = C_0 * P[0][1]; P[0][0] -= K_0 * t_0; P[0][1] -= K_0 * t_1; P[1][0] -= K_1 * t_0; P[1][1] -= K_1 * t_1; return kalman_filter_angle; }
融合之后的波形: