hashmap详解（基于jdk1.8）

简介：

在jdk1.8中，hashmap有了较大的优化，底层实现由之前的“数组+链表”改为了“数组+链表+红黑树”。jdk1.8的hashmap的数据结构如图所示，当链表节点较少时仍然以链表形式存在，当链表节点较多时（大于8）会转化为红黑树。

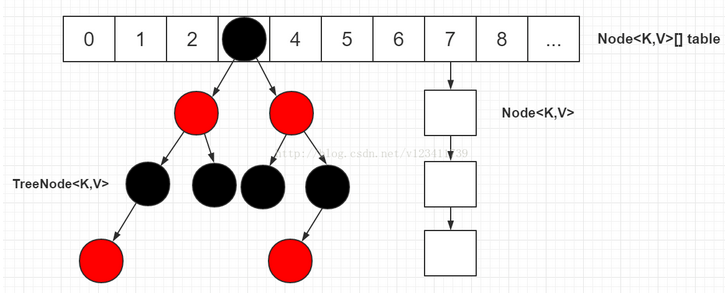
重要知识点：

1、文章中头节点指的是table表上索引位置的节点，也就是链表的头结点

2、根节点（root）指的是红黑树最上面的节点，也就是没有父节点的节点

3、红黑树的根节点不一定是索引位置的头结点（链表的头结点），hashmap通过moveRootToFront方法来维持红黑树的根节点就是索引位置的头结点，但是在removeTreeNode方法中，当movable为false时，不会调用moveRootToFront方法，此时红黑树的根节点不一定是索引位置的头结点，该情形发生在hashIterator的remove方法中

4、转为红黑树之后，链表的结构还存在，通过next属性维持，红黑树节点在进行操作时都会维护链表的结构，并不是转化为红黑树节点，链表结构就不存在了

5、在红黑树上，叶子节点也可能有next节点，因为红黑树的结构与链表的结构是互不影响的，不会因为是叶子节点就说该节点已经没有next节点

6、源码中的一些变量的定义为：如果定义了一个节点p，则pl（p left）为p的左节点，pr（p right）为p的右节点，pp（p parent）为p的父节点，ph（p hash）为p的hash值，pk（p key）为p的key值，kc（key class）为key的类等等。

7、链表中移除一个节点只需要如图的操作

8、红黑树在维护链表结构时，移除一个节点只需要如图所示操作（红黑树中增加了一个prev属性），其他操作同理。注：此处只是红黑树维护链表结构的操作，红黑树还需要单独进行红黑树的移除或者其他操作

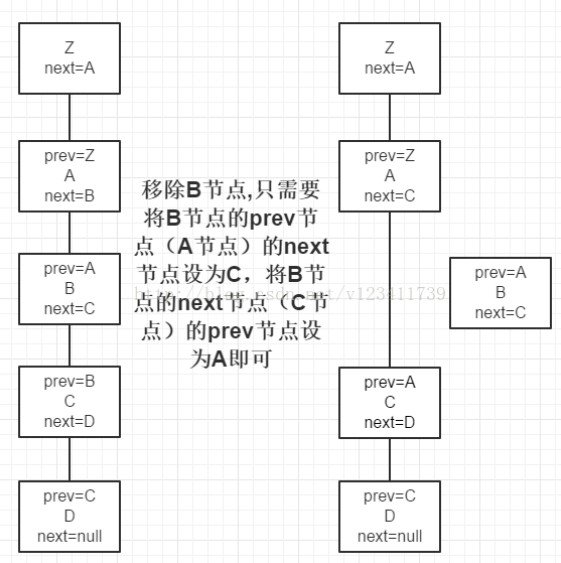
9、源码中进行红黑树的查找时，会反复使用两条规则：1）如果目标节点的hash值小与p节点的hash值，则向p节点的左边遍历；否则向p节点的右边遍历。2）如果目标节点的key值小与p节点的key值，则向p节点的左边遍历；否则向p节点的右边遍历。这两条规则是利用了红黑树的特性（左节点<根节点<右节点）

10、源码中进行红黑树的查找时，会用dir（direction）来表示向左还是向右查找，dir存储的值是目标节点的hash/key与p节点的hash/key的比较结果

基本属性：

// 默认容量16
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; 
 
// 最大容量
static final int MAXIMUM_CAPACITY = 1 << 30;    
 
// 默认负载因子0.75
static final float DEFAULT_LOAD_FACTOR = 0.75f; 
 
// 链表节点转换红黑树节点的阈值, 9个节点转
static final int TREEIFY_THRESHOLD = 8; 
 
// 红黑树节点转换链表节点的阈值, 6个节点转
static final int UNTREEIFY_THRESHOLD = 6;   
 
// 转红黑树时, table的最小长度
static final int MIN_TREEIFY_CAPACITY = 64; 
 
// 链表节点, 继承自Entry
static class Node<K,V> implements Map.Entry<K,V> {  
    final int hash;
    final K key;
    V value;
    Node<K,V> next;
 
    // ... ...
}
 
// 红黑树节点
static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
    TreeNode<K,V> parent;  // red-black tree links
    TreeNode<K,V> left;
    TreeNode<K,V> right;
    TreeNode<K,V> prev;    // needed to unlink next upon deletion
    boolean red;
   
    // ...
}

定位哈希桶数组索引位置

由于HashMap的数据结构为“数组+链表+红黑树”的组合，所以我们希望这个HashMap里面的元素位置尽量分布地更加均匀，尽量使得每个位置上的元素数量只有一个，那么当我们用hash算法求得这个位置的时候，马上就可以知道对应位置的元素就是我们要的，不用遍历链表/红黑树，大大优化了查询的效率。HashMap定位数组索引的位置，直接决定了hash方法的离散性能。源码为：

// 代码1
static final int hash(Object key) { // 计算key的hash值
    int h;
    // 1.先拿到key的hashCode值; 2.将hashCode的高16位参与运算
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
// 代码2
int n = tab.length;
// 将(tab.length - 1) 与 hash值进行&运算
int index = (n - 1) & hash;

1、拿到key的hashCode值

2、将hashCode的高位参与运算，重新计算hash值

3、将计算出来的hash值于（table.length-1)进行&运算

解读：对于任意给定的对象，只要他的hashCode()返回值相同，那么计算得到的hash值总是相同的。把hash值对table长度取模运算，这样一来，元素的分布相对来说是比较均匀的。

但是模运算的消耗比较大，计算机中的位运算比较快，因此使用代码2的位与运算来代替模运算。他通过(table.length-1)&h来获得该对象的索引位置。

在JDK1.8的实现中，还优化了高位运算的算法，将hashCode的高16位与hashCode进行异或运算，主要是为了在table的长度较小的时候，让高位也参与运算，并且不会有太大的开销。

例子：

当table的长度为16时，table.length-1=15，在二进制中，此时低四位全部为1，高28位全部为0，当0进行&运算时结果必然为0，因此此时hashCode与“table.length-1”的&运算只取决于hashCode的低四位，在这种情况下，hashCode的高28位就没起到任何作用，并且由于hash结果只取决于hashCode的低4位，hash冲突的概率也会增加。因此，在JDK1.8中，将高位也参与计算，目的是为了降低hash冲突的概率。

 get方法：

public V get(Object key) {
    Node<K,V> e;
    return (e = getNode(hash(key), key)) == null ? null : e.value;
}
 
final Node<K,V> getNode(int hash, Object key) {
    Node<K,V>[] tab; Node<K,V> first, e; int n; K k;
    // 1.对table进行校验：table不为空 && table长度大于0 && 
    // table索引位置(使用table.length - 1和hash值进行位与运算)的节点不为空
    if ((tab = table) != null && (n = tab.length) > 0 &&
        (first = tab[(n - 1) & hash]) != null) {
        // 2.检查first节点的hash值和key是否和入参的一样，如果一样则first即为目标节点，直接返回first节点
        if (first.hash == hash && // always check first node
            ((k = first.key) == key || (key != null && key.equals(k))))
            return first;
        // 3.如果first不是目标节点，并且first的next节点不为空则继续遍历
        if ((e = first.next) != null) {
            if (first instanceof TreeNode)
                // 4.如果是红黑树节点，则调用红黑树的查找目标节点方法getTreeNode
                return ((TreeNode<K,V>)first).getTreeNode(hash, key);
            do {
                // 5.执行链表节点的查找，向下遍历链表, 直至找到节点的key和入参的key相等时,返回该节点
                if (e.hash == hash &&
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    return e;
            } while ((e = e.next) != null);
        }
    }
    // 6.找不到符合的返回空
    return null;
}

4.如果是红黑树节点，则调用红黑树的查找目标节点方法 getTreeNode。

final TreeNode<K,V> getTreeNode(int h, Object k) {
    // 1.首先找到红黑树的根节点；2.使用根节点调用find方法
    return ((parent != null) ? root() : this).find(h, k, null);
}

2.使用根节点调用 find 方法。

/**
 * 从调用此方法的节点开始查找, 通过hash值和key找到对应的节点
 * 此方法是红黑树节点的查找, 红黑树是特殊的自平衡二叉查找树
 * 平衡二叉查找树的特点：左节点<根节点<右节点
 */
final TreeNode<K,V> find(int h, Object k, Class<?> kc) {
    // 1.将p节点赋值为调用此方法的节点，即为红黑树根节点
    TreeNode<K,V> p = this;
    // 2.从p节点开始向下遍历
    do {
        int ph, dir; K pk;
        TreeNode<K,V> pl = p.left, pr = p.right, q;
        // 3.如果传入的hash值小于p节点的hash值，则往p节点的左边遍历
        if ((ph = p.hash) > h)
            p = pl;
        else if (ph < h) // 4.如果传入的hash值大于p节点的hash值，则往p节点的右边遍历
            p = pr;
        // 5.如果传入的hash值和key值等于p节点的hash值和key值,则p节点为目标节点,返回p节点
        else if ((pk = p.key) == k || (k != null && k.equals(pk)))
            return p;
        else if (pl == null)    // 6.p节点的左节点为空则将向右遍历
            p = pr;
        else if (pr == null)    // 7.p节点的右节点为空则向左遍历
            p = pl;
        // 8.将p节点与k进行比较
        else if ((kc != null ||
                  (kc = comparableClassFor(k)) != null) && // 8.1 kc不为空代表k实现了Comparable
                 (dir = compareComparables(kc, k, pk)) != 0)// 8.2 k<pk则dir<0, k>pk则dir>0
            // 8.3 k<pk则向左遍历(p赋值为p的左节点), 否则向右遍历
            p = (dir < 0) ? pl : pr;
        // 9.代码走到此处, 代表key所属类没有实现Comparable, 直接指定向p的右边遍历
        else if ((q = pr.find(h, k, kc)) != null) 
            return q;
        // 10.代码走到此处代表“pr.find(h, k, kc)”为空, 因此直接向左遍历
        else
            p = pl;
    } while (p != null);
    return null;
}

 明天再写