自动训练（决策树）模型

项目上要求给出一个可配置的类自动化的流程，下面根据自己的思考给出自动训练模型的部分。

决策树模型关键参数有两个：树深度和树棵数（模型训练中称为迭代次数，下称迭代次数）

树深度

树的深度如何决定，个人觉得：每棵树最好都能用到所有的特征，所以树深度跟特征数相关，对特征个数对2求对数，然后上取整即可

# 通过特征个数计算决策树深度
# 计算逻辑：把所有的特征都放到决策树的叶子节点至少需要深度为多少的二叉树
tree_depth = math.ceil(math.log(num_of_features,2))

下面做了一个验证这样选择树深度合理的实验

特征个数:6，正样本：2903，计算得到树深度为3，最大迭代次数（看下面）为47

先看树深度为2，3，4的评分结果：y是评分结果，t是train_fbeta，e是eval_fbeta

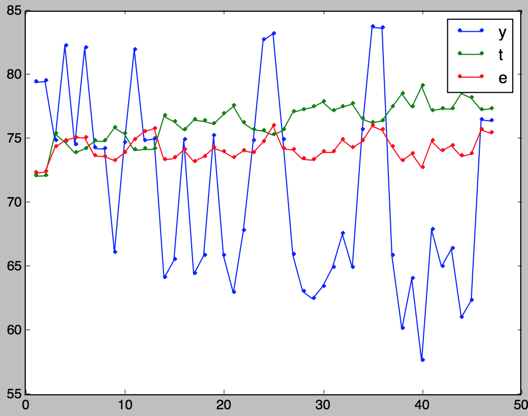
树深度为2：

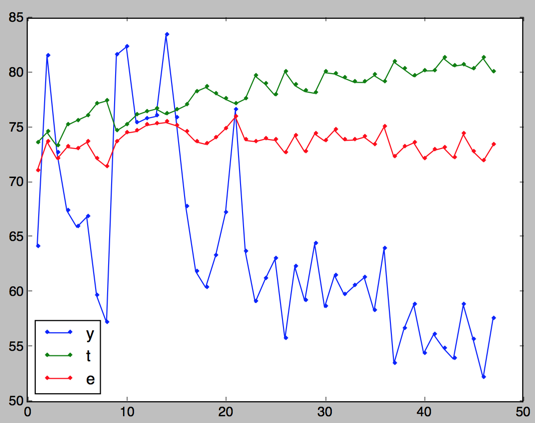
树深度为3

树深度为4：

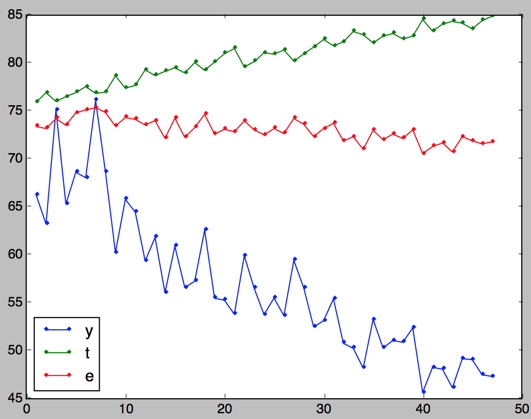
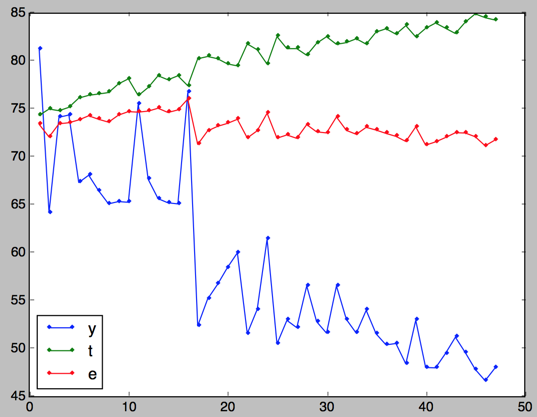
这个实验也证明这样选择树深度是比较合理的：

树深度过小，模型不容易收敛，需要更大的迭代次数；

树深度过大，模型容易过拟合，甚至可能在迭代次数为一的时候就已经过拟合。

对比树深度为2，3，4的结果，可以发现树深度为3的时候比较合理，没有一开始就过拟合，也不需要太大的迭代次数再能收敛。 

迭代次数

相对树深度来说，迭代次数不好确定，是本文的重点，下面详细给出自己的做法

上下限

下限比较容易，至少也得生成一一棵决策树，下限可以定为1，当然，如果你知道更高的下限，那就更好不过了

上限可以根据经验来，详细见下面的注释。

    # 通过样本数和特征数（树深度）计算最大的迭代次数
    # 计算逻辑是：每个特征需要多少个样本来支撑（这个需要根据样本本身和实践经验得到）
    # 这里我们使用正样本的数量来计算，根据经验，每个特征我们假设需要10个样本支撑（这个值可以根据不同的样本来选择）
    # 样本越多，样本越密集，每个特征需要支撑的样本数增加
    sustain_num = 10
    max_num_rounds= pos_num/(num_of_features*sustain_num)

模型好坏

模型本身好坏

这里只研究二分类问题，对于给定的样本，模型的好坏还是有比较成熟的标准去判断，比较精度和召回率，fbeta值等等

一般来说精度和召回率是此起彼伏的关系，所以一般用他们的加权值fbeta来衡量

from sklearn import metrics

# 二分类问题的fbeta，在这里作为衡量训练模型好坏的标准，而不是直接用精度和召回率
def getFbeta(train_y,predict):
    # print set(train_y),set(predict)
    return metrics.fbeta_score(train_y, predict, 0.5,labels=[0,1])

模型鲁棒性

一般随着迭代次数的增加，模型趋向过拟合，也就是模型本身会过分拟合训练数据，导致可能在其他的样本集表现失常，从而使得模型鲁棒性差。

鲁棒性强的模型在训练集和测试集（有人叫评价集或者验证集）表现稳定，

下面定义了一个衡量模型好坏的函数，综合评价了模型本身的好坏(train_fbeta)和鲁棒性(train_fbeta-eval_fbeta)

不同的数据集模型可能表现不一样，可以根据自己的需要修改评分函数

# fbeta是衡量模型训练结果的好坏，训练集的fbeta一般要比验证集的高，因为模型使用训练集训练出来的，一般会更加拟合训练集
# 这个函数主要是通过模型在验证集上的表现和在训练集的表现，给出该模型最后的总评分
# 例如 （74.5%，74.6%）跟（84%，85%）那个结果更优？
# 设计逻辑：我们认为差值在1%之内是比较可以接受的，在差值≤1%的时候，均值越大越好，当差值>1%的时候，我们更倾向于差值≤1%的模型，
# 同时，差值≤1%的时候，我们不会计较具体值是多少
# 也就是说，差值≤1%的模型我们倾向于给出更高的评分，给出几个例子吧
#  组1             组2             更优（？只是直观感觉）    
#  (74.5%, 74.6%)  (84.0%, 85.0%) (84.0%, 85.0%)
#  (64.5%, 64.9%)  (88.0%, 85.0%) (64.5%, 64.6%)
#  (64.5%, 64.6%)  (66.3%, 66.6%) (66.3%, 66.6%)
#  (63.5%, 64.6%)  (72.3%, 68.6%) (63.5%, 64.6%)

def eval_model(train_fbeta,eval_fbeta):
    difference = abs(train_fbeta-eval_fbeta)
    average = (train_fbeta+eval_fbeta)/2.0
    if difference <= 1.0:
        return fbeta_weights*average
    elif difference > 1.0 and difference <=2.0:
        return average
    else:
        return average/(1+difference/20.0)

自动训练模型

最坏的情况是不知道模型在什么时候会达到最优，这个时候我们必须遍历所有的迭代次数才能得到最优的迭代次数和最好的模型。

一般情况下，随着迭代次数的增加，评分会先上升后下降，有最大值；并且在最大值之后评分会持续下降。

如果实验次数够多，树深度选择合理，期待的评分曲线是一个先陡坡后缓坡的形状，这种情况下我们提前结束模型的训练。

# 能够自动训练的核心理论基础是：随着迭代次数的增加，评分会先上升后下降，有最大值；并且在最大值之后评分会持续下降
# 所以只需要判断在到达一个极大值之后，如果在可以接受的一段区间内评分都下降，就可以认为这个极大值就是最大值（这里我们认为如果20次都没有比极大值更大的，那么这个极大值就是最大值）
def auto_train(dtrain,tree_depth,min_num_rounds,max_num_rounds):
    max_score=-1;max_score_num_round=0;
    label=0
    for i in xrange(min_num_rounds,max_num_rounds):
        score = train(dtrain, tree_depth, i, train_rounds)
        if score > max_score:
            max_score = score
            max_score_num_round = i 
            label=0
        label+=1
        if label>=20:
            break
    return max_score_num_round,max_score

模型重现 

由于模型训练具有偶然性，我们不直接使用自动训练模型的结果，而是采用自动训练模型给出的最优树深度和迭代次数重新训练模型，

如果可以重现最优结果，那么我们就可以认为自动训练出来的模型是可靠的；反之，如果，重新训练模型很久都不能重现自动训练的最优结果，我们认为这次自动训练模型的结果具有较大的偶然性，需要重新自动训练模型

    while True:
        if abs(best_score -best_train(dtrain, tree_depth, num_round))<1.0:
            print "决策树深度:",tree_depth
            print "迭代次数:",num_round
            print "train_fbeta:",res_list[num_round-1][1]
            print "eval_fbeta:",res_list[num_round-1][2]
            print "best_score:",best_score
            break
        count+=1
        if count>20:
            print "auto rerun!"
            os.system("rm model_depth{0}_{1}trees_{2}".format(int(tree_depth), num_round, datetime.datetime.now().strftime('%Y-%m-%d')))
            os.system("python auto_train.py")
            break

至此，自动训练决策树模型基本成型，下面附上完整的代码，供参考。

# auto_train.py
# coding:utf8
import os,sys,time,math
import numpy as np 
import xgboost as xgb
import datetime
from sklearn import metrics
from sklearn.metrics import classification_report
ISOTIMEFORMAT='%Y-%m-%d %X'

fbeta_difference=1.0
fbeta_weights=1.1
train_rounds=3

res_list=[]

def getFbeta(train_y,predict):
    return metrics.fbeta_score(train_y, predict, 0.5,labels=[0,1])

def eval_model(train_fbeta,eval_fbeta):
    difference = abs(train_fbeta-eval_fbeta)
    average = (train_fbeta+eval_fbeta)/2.0
    if difference <= 1.0:
        return fbeta_weights*average
    elif difference > 1.0 and difference <=2.0:
        return average
    else:
        return average/(1+difference/20.0)

def loadfile(filename):
    X, y = [], []
    count = 0;
    fields = 0;
    with open(filename) as f:
        fields= len(f.readline().strip("
").split("	"))
    with open(filename) as f:
        for line in f:
            try:
                line = line.strip("
").split('	')
                if len(line)!=fields:
                    continue
                X.append([float(item) for item in line[1:]])
                y.append(int(line[0]))
                count += 1
            except:
                print traceback.format_exc()
    data = xgb.DMatrix(X, label=y)
    return data,count,fields-1

def train(dtrain, max_depth, num_rounds, train_rounds):
    train_fbeta_list=[];eval_fbeta_list=[]
    for x in xrange(0,train_rounds):
        shuffled_idx = range(dtrain.num_row())
        np.random.seed(time.localtime())
        np.random.shuffle(shuffled_idx)
        dsubtrain = dtrain.slice(shuffled_idx[:len(shuffled_idx) / 2 + 1])
        dsubeval = dtrain.slice(shuffled_idx[len(shuffled_idx) / 2 + 1:])
        param = {'max_depth': int(max_depth), 'eta': 1, 'silent': 1, 'objective': 'binary:logistic'}
        watchlist = [(dsubeval, 'eval'), (dsubtrain, 'train')]
        num_rounds = int(num_rounds)
        bst = xgb.train(param, dsubtrain, num_rounds, watchlist)

        leafindex = bst.predict(dsubtrain, output_margin=True, pred_leaf=False)
        pred_res = [1 if index > 0.5 else 0 for index in leafindex]
        train_fbeta_list.append(getFbeta(dsubtrain.get_label(), pred_res))

        leafindex = bst.predict(dsubeval, output_margin=True, pred_leaf=False)
        pred_res = [1 if index > 0.5 else 0 for index in leafindex]
        eval_fbeta_list.append(getFbeta(dsubeval.get_label(), pred_res))
    train_fbeta=sum(train_fbeta_list)/len(train_fbeta_list)*100
    eval_fbeta=sum(eval_fbeta_list)/len(eval_fbeta_list)*100
    score=eval_model(train_fbeta,eval_fbeta)
    res_list.append([num_rounds,train_fbeta,eval_fbeta,score])
    return score

def best_train(dtrain, max_depth, num_rounds):
    shuffled_idx = range(dtrain.num_row())
    np.random.seed(time.localtime())
    np.random.shuffle(shuffled_idx)
    dsubtrain = dtrain.slice(shuffled_idx[:len(shuffled_idx) / 2 + 1])
    dsubeval = dtrain.slice(shuffled_idx[len(shuffled_idx) / 2 + 1:])
    param = {'max_depth': int(max_depth), 'eta': 1, 'silent': 1, 'objective': 'binary:logistic'}
    watchlist = [(dsubeval, 'eval'), (dsubtrain, 'train')]
    num_rounds = int(num_rounds)
    bst = xgb.train(param, dsubtrain, num_rounds, watchlist)
    bst.save_model(
        "model_depth{0}_{1}trees_{2}".format(int(max_depth), num_rounds, datetime.datetime.now().strftime('%Y-%m-%d')))

    leafindex = bst.predict(dsubtrain, output_margin=True, pred_leaf=False)
    pred_res = [1 if index > 0.5 else 0 for index in leafindex]
    train_fbeta = getFbeta(dsubtrain.get_label(), pred_res)*100

    leafindex = bst.predict(dsubeval, output_margin=True, pred_leaf=False)
    pred_res = [1 if index > 0.5 else 0 for index in leafindex]
    eval_fbeta = getFbeta(dsubeval.get_label(), pred_res)*100
    score=eval_model(train_fbeta,eval_fbeta)
    return score

def auto_train(dtrain,tree_depth,min_num_rounds,max_num_rounds):
    max_score=-1;max_score_num_round=0;
    label=0
    for i in xrange(min_num_rounds,max_num_rounds):
        score = train(dtrain, tree_depth, i, train_rounds)
        if score > max_score:
            max_score = score
            max_score_num_round = i 
            label=0
        label+=1
        if label>=20:
            break
    return max_score_num_round,max_score

if __name__ == '__main__':

    filename="oldtrain10"
    dtrain,count,num_of_features=loadfile(filename)

    tree_depth = math.ceil(math.log(num_of_features,2))
    pos_num = sum(dtrain.get_label())
    sustain_num = 10
    max_num_rounds= pos_num/(num_of_features*sustain_num)

    num_round,best_score=auto_train(dtrain, tree_depth, 1, int(max_num_rounds))
    count=0
    while True:
        if abs(best_score -best_train(dtrain, tree_depth, num_round))<1.0:
            print "决策树深度:",tree_depth
            print "迭代次数:",num_round
            print "train_fbeta:",res_list[num_round-1][1]
            print "eval_fbeta:",res_list[num_round-1][2]
            print "best_score:",best_score
            break
        count+=1
        if count>20:
            print "auto rerun!"
            os.system("rm model_depth{0}_{1}trees_{2}".format(int(tree_depth), num_round, datetime.datetime.now().strftime('%Y-%m-%d')))
            os.system("python auto_train.py")
            break