1.P1453城市环路
题目背景
一座城市,往往会被人们划分为几个区域,例如住宅区、商业区、工业区等等。B市就被分为了以下的两个区域——城市中心和城市郊区。在着这两个区域的中间是一条围绕B市的环路,环路之内便是B市中心。
题目描述
整个城市可以看做一个N个点,N条边的单圈图(保证图连通),唯一的环便是绕城的环路。保证环上任意两点有且只有2条路径互通。图中的其它部分皆隶属城市郊区。
现在,有一位名叫Jim的同学想在B市开店,但是任意一条边的2个点不能同时开店,每个点都有一定的人流量Pi,在该点开店的利润就等于该店的人流量Pi×K(K≤10000),K的值将给出。
Jim想尽量多的赚取利润,请问他应该在哪些地方开店?
输入格式
第一行一个整数N 代表城市中点的个数。城市中的N个点由0~N-1编号。
第二行N个正整数,表示每个点的人流量Pi(Pi≤10000)。
下面N行,每行2个整数A,B,表示A,B建有一条双向路。
最后一行一个实数K。
输出格式
一个实数M,(保留1位小数),代表开店的最大利润。
输入输出样例
4 1 2 1 5 0 1 0 2 1 2 1 3 2
12.0
说明/提示
【数据范围】
对于20%的数据,N≤100.
对于另外20%的数据,环上的点不超过2000个
对于50%的数据 N≤50000.
对于100%的数据 N≤100000.
前置知识
基环树
我们都知道,出题人都以出出有意义的题目为己任【其实就是毒瘤
当我们可以熟练掌握图上和树上的任务的时候,出题人不爽了。
某一天,某位毒瘤出题人在深夜被汽车吵醒,之后终于发现一个神奇的东西。
集树形结构和环路于一体,又不至于不可做的东西。
基环树!!!
【上面都是我自己yy的QAQ
不管过程究竟是什么样子的了,总之,我们现在有可能考这个奇怪的东西。
究竟什么是基环树呢?
私自定义1:
在一棵树上面,加一条边,形成一颗只含有一个环的树【雾
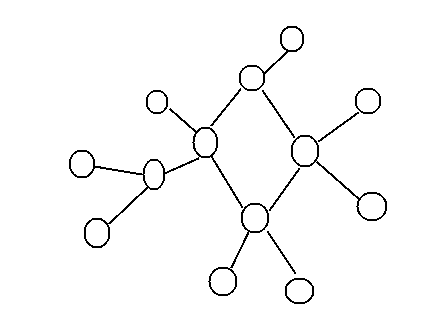
比如这张图。【对不起我又盗图了QAQ
私自定义2:
一张只有一个环的图。
既然可以看成一张图,我们都知道图是可以有向的。
那么基环树也是可以有向的。

指向环的:内向基环树
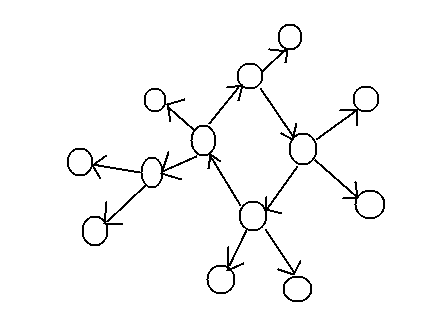
起源于环的:外向基环树。
那么怎么才能解决这种问题呢?一会在题面中解释吧。
本题思路分析
我们从题面中有这样一句话:
N条边的单圈图(保证图连通),唯一的环便是绕城的环路。
这说明了什么?
构想一下地图的场景,假设只有一个环,那么这张图就是一颗基环树。
啊啊啊,好希望这能是一颗树啊?
这样就能采取树形DP了啊QAQ
emmm,好像是有办法的,指变成树。
我们仔细想想,这是一颗在树上加了一条边形成的结构。
如果想重新变成一颗树,那么直接删边不就好了嘛?
那么究竟删哪条边才合适呢?
删环上的边是无疑的,毕竟要保证图的的连通性。
但是,环上的边有那么多条,难道要全部都删一遍吗?
当然不可能啊?怎么证明呢?
实际上,我们考虑树形DP本身的一些性质。
我们定义 f [ i ] 数组来记录以 i 为根的子树的性质。
然后,我们可以任意选择一条边,分别从这条边的左右端点各跑一次树形DP。
这样我们可以得到两个数组,f [ ],f ' [ ]
但是由于本身定义是重合的,所以,这个数组维护的信息就同时包括着:
1. 左节点选,右节点不选
2. 左节点不选,右节点选
3. 左右节点都不选
这三种情况,刚好把不满足题意的“都选”操作给忽略了,正好是我们所需要的。
那么自然,跑两遍tree DP就OK了。
AC代码放送

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<algorithm> 6 #define ll long long 7 #define uint unsigned int 8 using namespace std; 9 10 const int MA=1e6+10; 11 ll n,val[MA]; 12 struct ss{ 13 ll to,nxt; 14 }tr[MA*2]; 15 ll head[MA],ecnt=1; 16 17 inline void add(ll a,ll b) { 18 tr[++ecnt].nxt=head[a]; 19 tr[ecnt].to=b; 20 21 head[a]=ecnt; 22 return; 23 } 24 25 ll sta,ed,bian; 26 27 28 bool vis[MA]; 29 30 void dfs(ll x,ll fa) { 31 vis[x]=1; 32 for(uint i=head[x];i;i=tr[i].nxt) { 33 ll y=tr[i].to; 34 if(y==fa) 35 continue; 36 if(vis[y]) { 37 sta=x; 38 ed=y; 39 bian=i; 40 41 42 continue; 43 } 44 dfs(y,x); 45 } 46 return; 47 } 48 49 double f[MA][2]; 50 51 void dp(ll x,ll fa) { 52 f[x][0]=0; 53 f[x][1]=val[x]; 54 for(uint i=head[x];i;i=tr[i].nxt) { 55 ll y=tr[i].to; 56 if(i==bian||i==(bian^1)) 57 58 continue; 59 if(y==fa) 60 continue; 61 dp(y,x); 62 f[x][0]+=max(f[y][0],f[y][1]); 63 f[x][1]+=f[y][0]; 64 } 65 return; 66 } 67 68 int main() 69 { 70 scanf("%lld",&n); 71 72 for(uint i=1;i<=n;i++) 73 scanf("%lld",&val[i]); 74 for(uint i=1;i<=n;i++) { 75 ll x,y; 76 scanf("%lld%lld",&y,&x); 77 78 x++,y++; 79 add(y,x); 80 81 add(x,y); 82 83 } 84 double k; 85 scanf("%lf",&k); 86 87 double ans=0; 88 dfs(1,1); 89 dp(sta,sta); 90 double tmp=f[sta][0]; 91 dp(ed,ed); 92 ans+=max(tmp,f[ed][0]); 93 printf("%.1lf ",ans*k); 94 return 0; 95 }
2.骑士
题目描述
Z国的骑士团是一个很有势力的组织,帮会中汇聚了来自各地的精英。他们劫富济贫,惩恶扬善,受到社会各界的赞扬。
最近发生了一件可怕的事情,邪恶的Y国发动了一场针对Z国的侵略战争。战火绵延五百里,在和平环境中安逸了数百年的Z国又怎能抵挡的住Y国的军队。于是人们把所有的希望都寄托在了骑士团的身上,就像期待有一个真龙天子的降生,带领正义打败邪恶。
骑士团是肯定具有打败邪恶势力的能力的,但是骑士们互相之间往往有一些矛盾。每个骑士都有且仅有一个自己最厌恶的骑士(当然不是他自己),他是绝对不会与自己最厌恶的人一同出征的。
战火绵延,人民生灵涂炭,组织起一个骑士军团加入战斗刻不容缓!国王交给了你一个艰巨的任务,从所有的骑士中选出一个骑士军团,使得军团内没有矛盾的两人(不存在一个骑士与他最痛恨的人一同被选入骑士军团的情况),并且,使得这支骑士军团最具有战斗力。
为了描述战斗力,我们将骑士按照1至N编号,给每名骑士一个战斗力的估计,一个军团的战斗力为所有骑士的战斗力总和。
输入格式
输入文件knight.in第一行包含一个正整数N,描述骑士团的人数。
接下来N行,每行两个正整数,按顺序描述每一名骑士的战斗力和他最痛恨的骑士。
输出格式
输出文件knight.out应包含一行,包含一个整数,表示你所选出的骑士军团的战斗力。
输入输出样例
3 10 2 20 3 30 1
30
说明/提示
对于30%的测试数据,满足N ≤ 10;
对于60%的测试数据,满足N ≤ 100;
对于80%的测试数据,满足N ≤ 10 000。
对于100%的测试数据,满足N ≤ 1 000 000,每名骑士的战斗力都是不大于 1 000 000的正整数
思路 分析
通过观察题面,我们发现,这张图上面很有可能不止一个环,甚至可能不是联通的。
但是,可以感性理解一下,对于每一个联通块,有且仅有一个环。
为什么呢?
因为,每个节点都要有一条出边【我恨他,和很多条入边【大家都恨我
那么有资格向下发出一条出边的节点也就是根节点了。
如此一来,这就是一片基环树森林。
既然有了基环树这么一个优秀的性质,对于森林只需要保证全部的树都被遍历到就好了。
最后还有一点,本题的图不是有向图,恨的关系看起来是单向的,但本质上是双向的。
比如说A恨B,然后B知道A恨他,于是也不想跟A一块走。【由爱生恨?
AC代码放送

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<algorithm> 6 #define ll long long 7 #define uint unsigned int 8 using namespace std; 9 10 const int MA=1e6+10; 11 ll n,val[MA]; 12 struct ss{ 13 ll to,nxt; 14 }tr[MA*2]; 15 ll head[MA],ecnt=1; 16 17 inline void add(ll a,ll b) { 18 tr[++ecnt].nxt=head[a]; 19 tr[ecnt].to=b; 20 21 head[a]=ecnt; 22 return; 23 } 24 25 ll sta,ed,bian; 26 27 bool vis[MA]; 28 29 void dfs(ll x,ll fa) { 30 vis[x]=1; 31 for(uint i=head[x];i;i=tr[i].nxt) { 32 ll y=tr[i].to; 33 if(y==fa) 34 continue; 35 if(vis[y]) { 36 sta=x; 37 ed=y; 38 bian=i; 39 40 continue; 41 } 42 dfs(y,x); 43 } 44 return; 45 } 46 47 ll f[MA][2]; 48 49 void dp(ll x,ll fa) { 50 f[x][0]=0; 51 f[x][1]=val[x]; 52 for(uint i=head[x];i;i=tr[i].nxt) { 53 ll y=tr[i].to; 54 if(i==bian||i==(bian^1)) 55 56 continue; 57 if(y==fa) 58 continue; 59 dp(y,x); 60 f[x][0]+=max(f[y][0],f[y][1]); 61 f[x][1]+=f[y][0]; 62 } 63 return; 64 } 65 66 int main() 67 { 68 scanf("%lld",&n); 69 70 for(uint i=1;i<=n;i++) { 71 ll x; 72 scanf("%lld%lld",&val[i],&x); 73 74 add(i,x); 75 76 add(x,i); 77 78 } 79 ll ans=0; 80 for(uint i=1;i<=n;i++) { 81 if(vis[i]) 82 continue; 83 dfs(i,i); 84 dp(sta,sta); 85 ll tmp=f[sta][0]; 86 dp(ed,ed); 87 ans+=max(tmp,f[ed][0]); 88 } 89 printf("%lld ",ans); 90 return 0; 91 }
最后的建议
提交代码之前一定要看好dfs函数,有没有出现无线递归的情况,不然会MLE。QAQ
祝大家AC愉快!
