Solution -「ARC 104F」Visibility Sequence

(mathcal{Description})

  Link.

  给定 ({x_n})，对于满足 (h_iin[1,x_i]) 的序列 ({h_n})，定义序列 ({p_n}) 满足：

[p_i=egin{cases}-1,&( otexist j<i)(h_j>h_i)\max_{j<i}{j|h_j>h_i},& ext{otherwise}end{cases} ]

  求所有可能出现的本质不同的 ({p_n})，对 (10^9+7) 取模。

  (nle100)。

(mathcal{Solution})

  ({p_n}) 是一个下标对应关系，所以可以尝试着把关系化成图。正如 PKU 面试的那位老师所说：“图表示关系”。

  但 (-1) 明显很丑，令 (a_0=+infty)，那么对于 ({+infty,3,1,2,5,4})，({p}) 长成：

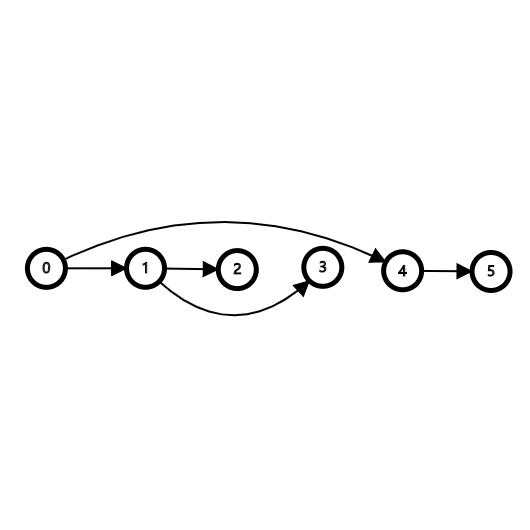
  多画几个目测一下，得到：

1. 图是一棵以 (0) 为根的外向树（废话。
2. 以 (u) 为根，大小为 (s) 的子树对应原序列的区间 ([u,u+s))。还可以用 DFN 描述：存在一种对于所有 (i)，(operatorname{dfn}(i)=i) 的 DFS 顺序。

  简证结论二：归纳证明，考虑 DFS 到 (u) 点后，是否一定存在一种方案，下一步 DFS 到 (u+1)：

• 若 (h_u>h_{u+1})，有直接连边，满足。
• 若 (h_ule h_{u+1})，则显然不存在 (w>u+1)，使得 (langle u,w anglein E)。所以 DFS 返回过程中，除非满足上一条件走向 (u+1)，否则不可能走向其他 (>u) 的结点。证毕。

  从计数的角度考虑，({p}) 相等则代表这颗树的树形完全一样。所以可以对于每种树形，构造一个最可能存在的 ({h_n})（所有值尽量小），只对这种 ({h_n}) 计数，就能实现不重不漏。归纳构造：

• 对于叶子 (u)，显然 (h_u=1) 最合适。
• 对于非叶 (u)，应满足 (h_ugemax_{vin son_u}{h_v}+1)；其次若再 (u) 的左侧有同父亲的兄弟 (w)，则还要满足 (h_uge h_w)，可以结合上图理解。所以直接钦定 (h_u=max{h_w,max_{vin son_u}{h_v}+1})。根据此构造方式，(h_u) 变小不会导致子树外 (h) 变大，所以这种构造能得到最可能存在的 ({h_n})。注意上式也有一个重要的性质，(operatorname{arg}max_{vin son_u}{h_v}) 为 (u) 最右侧的儿子。

  举个例子，对于上图，构造出的 ({h_n}) 为 ({3,2,1,1,2,1})。

  走到现在都是凭感觉。

---

  由结论二，令 DP 状态 (f(l,r,k)) 表示区间 ([l,r]) 构成一棵以 (l) 为根且 (h_l=k) 的树的方案数；同时令 (g(l,r,k)) 为其第三维前缀和，即区间 ([l,r]) 构成一棵以 (l) 为根且 (h_lle k) 的树的方案数。

  转移，首先枚举位置 (p) 把区间分为 ([l,p)) 和 ([p,r])，由于最右侧儿子最大，(h_l=h_p+1)。分 (h_p) 原来与 ([l,p)) 中 (h_l) 的大小关系，有：

[f(l,r,k)=sum_{p=l+1}^rg(l,p-1,k)f(p,r,k-1)+[x_pge k-1]f(l,p-1,k)g(p,r,k-2) ]

  前一项表示 ([p,r]) 本身的 (h_p) 就为 (k-1)；后一项则表示 ([p,r]) 的 (h_p) 本身很小，但因为在左侧多了兄弟而被迫取到 (k-1)（所以要保证 (x_pge k-1)，有能力取到 (k-1)）；(f(l,p-1,k)f(p,r,k-1)) 可能算重所以最后一项是 (g(p,r,k-2))。

  最终，复杂度 (mathcal O(n^4))。（所以原题 (x_ile10^5) 拿来干嘛 qwq……

(mathcal{Code})

/* Clearink */

#include <cstdio>

const int MAXN = 100, MAXX = 1e5, MOD = 1e9 + 7;
int n, a[MAXN + 5];
int f[MAXN + 5][MAXN + 5][MAXN + 5], g[MAXN + 5][MAXN + 5][MAXN + 5];

inline int mul ( long long a, const int b ) { return a * b % MOD; }
inline int& addeq ( int& a, const int b ) { return ( a += b ) < MOD ? a : a -= MOD; }

int main () {
	scanf ( "%d", &n ), a[1] = ++ n;
	for ( int i = 2; i <= n; ++ i ) scanf ( "%d", &a[i] );
	for ( int i = 1; i <= n; ++ i ) {
		f[i][i][1] = 1;
		for ( int k = 1; k <= n; ++ k ) g[i][i][k] = 1;
	}
	for ( int len = 2; len <= n; ++ len ) {
		for ( int l = 1, r; ( r = l + len - 1 ) <= n; ++ l ) {
			for ( int x = 2; x <= n && x <= a[l]; ++ x ) {
				int& cur = f[l][r][x];
				for ( int p = l + 1; p <= r; ++ p ) {
					addeq ( cur, mul ( g[l][p - 1][x], f[p][r][x - 1] ) );
					if ( a[p] >= x - 1 ) {
						addeq ( cur, mul ( f[l][p - 1][x], g[p][r][x - 2] ) );
					}
				}
			}
			for ( int x = 1; x <= n; ++ x ) {
				addeq ( g[l][r][x] = g[l][r][x - 1], f[l][r][x] );
			}
		}
	}
	printf ( "%d
", g[1][n][n] );
	return 0;
}

(mathcal{Details})

  随手画画图好习惯嗷！