LeetCode(3) || Median of Two Sorted Arrays
题记
之前做了3题,感觉难度一般,没想到突然来了这道比较难的,星期六花了一天的时间才做完,可见以前基础太差了。
题目内容
There are two sorted arrays A and B of size m and n respectively. Find the median of the two sorted arrays. The overall run time complexity should be O(log (m+n)).
解题思路
- 题目大致意思,有两个已经有序的数组A和B,他们的长度分别是m和n,现在要求获取两个数组的中位数且计算复杂度在O(log(m+n)).
- 题目意思比较简单,咋一想很好做么,但是考虑到时间复杂度O(log(m+n))的限制就略微有点困难了。
- 此题的难点主要在两个,一是计算复杂度,二是需要考虑很多边界情况,我在解题中就差点被淹没在无穷的边界情况中。
- 解此题我分别使用了三种方法,分别对应三种计算复杂度,O(nlog(n)),O(n),以及O(n)
- 第一种方法O(nlog(n))是最简单,大多数人使用的,即将数组A和数组B合并成数组C,对C进行排序再求中位数。按理说这样复杂度应该不符合题目的要求的,但是我抱着不死心的态度去LeetCode尝试了下,没想到就通过了。由此可见,LeetCode的运算时间并没有想象中的那么严格。
- 第二种方法O(n+m)需要进行一次遍历,在遍历的过程中,比较A[k]和B[i],以从小到大顺序为例,如果A[k]<B[i]则K++,否则i++。一直到k+i达到中位数的要求。此算法的难度在于需要考虑多种边界条件。
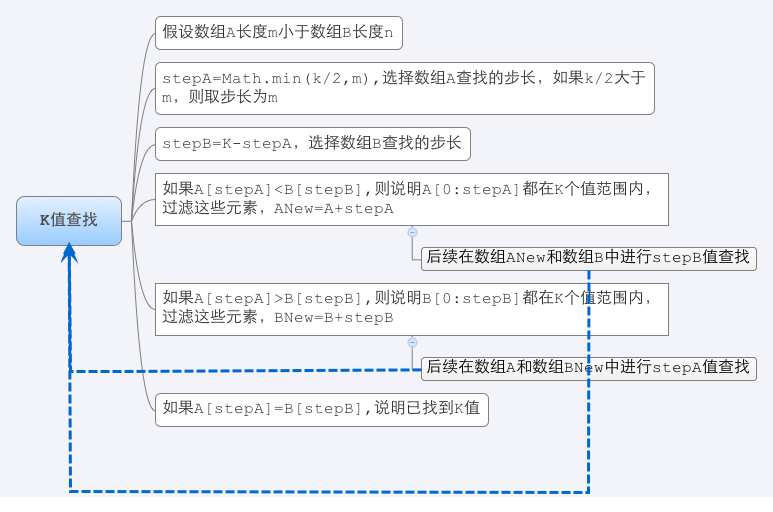
- 第三种方法O(log(m+n)),其实看到这个复杂度第一个反应就是对半查找,尝试了好久并未成功,后来才觉悟其实应该K值查找方法。算法内容大致如下:
- 判断中位数的类型,即m+n若为奇数,则查找第(m+n)/2个数,否则查找第(m+n)/2和第(m+n)/2+1个数。需要考虑数组为空的情况。
- 此时开始K值查找:
-
-
- K值查到其实就是查找第K个值的过程分解为查找第Min(K/2,m)和K-Min(K/2,m)两步,然后再递归进行下去。所以计算复杂度在O(log(m+n)).
- 另外需要注意的是还需要考虑几种边界条件:
- K=1时候,返回Min(A[0],B[0])
- m=0时候,返回B[k-1]
- m>n时候,需要互换数组A和数组B的位置。
-
解题方法
方法1:计算复杂度O(n*log(n))
1 public class Solution { 2 public double findMedianSortedArrays(int A[], int B[]) { 3 int m = A.length; 4 int n = B.length; 5 int[] C = new int[m+n]; 6 double median = 0; 7 System.arraycopy(A, 0, C, 0, A.length); 8 System.arraycopy(B, 0, C, A.length, B.length); 9 Arrays.sort(C); 10 11 if ( (m + n) % 2 == 0 ) { 12 median = (double)(C[(m+n)/2]+C[(m+n)/2-1])/2.0; 13 }else{ 14 median = C[(m+n-1)/2]; 15 } 16 17 return median; 18 } 19 }
方法2:计算复杂度O(n)
1 public class Solution { 2 public double findMedianSortedArrays(int A[], int B[]) { 3 int m = A.length; 4 int n = B.length; 5 int medianIndex1 = (m + n) % 2 == 0 ? (m+n)/2-1 :(m+n-1)/2; 6 int medianIndex2 = (m + n) % 2 == 0 ? (m+n)/2 :(m+n-1)/2; 7 int travelA = 0; 8 int travelB = 0; 9 double median = 0; 10 double median1 = 0; 11 double median2 = 0; 12 if ( m == 0 ){ 13 return n % 2 == 0 ? (double)(B[n/2]+B[n/2-1])/2:B[(n-1)/2]; 14 } 15 16 if( n == 0 ){ 17 return m % 2 == 0 ? (double) (A[m/2]+A[m/2-1])/2:A[(m-1)/2]; 18 } 19 20 for(int i = 0; i <= medianIndex2;i++){ 21 boolean flagA = true; 22 if ( travelA < m && travelB < n){ 23 if(A[travelA] >= B[travelB]){ 24 flagA = false; 25 }else{ 26 flagA = true; 27 } 28 }else if ( travelA >= m){ 29 flagA = false; 30 }else{ 31 flagA = true; 32 } 33 34 if (flagA){ 35 if ( i == medianIndex1 ){ 36 median1 = A[travelA]; 37 } 38 39 if ( i == medianIndex2 ){ 40 median2 = A[travelA]; 41 } 42 travelA++; 43 }else{ 44 if ( i == medianIndex1 ){ 45 median1 = B[travelB]; 46 } 47 48 if ( i == medianIndex2 ){ 49 median2 = B[travelB]; 50 } 51 travelB++; 52 } 53 } 54 55 if ( (m + n) % 2 == 0){ 56 median = (double) (median1 + median2)/2; 57 }else{ 58 median = median1; 59 } 60 61 return median; 62 } 63 }
方法3:计算复杂度O(log(m+n))
1 /** 2 * int A[] B[] ,数组A和数组B. 3 * int startA startB,子数组指针,子数组起始位置. 4 * int K, 需要查找的第K个值 5 * */ 6 public double findKthNum(int A[],int startA,int B[],int startB, int k){ 7 //获取数组A和数组B的子数组的数组长度 8 int m = A.length - startA; 9 int n = B.length - startB; 10 //假设数组A短于数组B,否则数组A和数组B互换位置。 11 if ( m > n){ 12 return findKthNum(B,startB,A,startA,k); 13 } 14 //数组A为空,第K个值从数组B的子串中获取 15 if ( m == 0 ){ 16 return B[startB+k-1]; 17 } 18 //只获取第一个数组,在数组A和数组B的子数组的第一个元素选择 19 if ( k == 1 ){ 20 return A[startA] > B[startB] ? B[startB] : A[startA]; 21 } 22 //将K值查找,分为min(k/2,m)和K-min(k/2,m)两步,考虑K/2>m这种情况 23 int newK = Math.min(k/2,m); 24 int leftK = k - newK; 25 26 if ( A[startA+newK-1] < B[startB+leftK-1] ){ 27 //数组A的子数组的前newK个元素都在K值范围内,过滤这new个元素继续查找第leftK个值 28 return findKthNum(A,startA+newK,B,startB,leftK); 29 }else if (A[startA+newK-1] > B[startB+leftK-1]){ 30 //数组B的子数组的前leftK个元素都在K值范围内,过滤这leftK个元素继续查找第k-leftK个值 31 return findKthNum(A,startA,B,startB+leftK,k-leftK); 32 }else{ 33 //如果相等,则说明找到中位数 34 return A[startA+newK-1]; 35 } 36 } 37 38 public double findMedianSortedArrays(int A[], int B[]) { 39 int m = A.length; 40 int n = B.length; 41 if ( m == 0 ){ 42 //数组A为空,则在数组B内直接查找中位数 43 return n % 2 == 0 ? (double)(B[n/2]+B[n/2-1])/2:B[(n-1)/2]; 44 } 45 46 if( n == 0 ){ 47 //数组B为空,则在数组A内直接查找中位数 48 return m % 2 == 0 ? (double) (A[m/2]+A[m/2-1])/2:A[(m-1)/2]; 49 } 50 51 if ( (m + n) %2 != 0){ 52 //m+n为奇数,查找第(m+n)/2+1个数 53 return findKthNum(A,0,B,0,(m+n)/2+1); 54 }else{ 55 //m+n为偶数,查找第(m+n)/2合(m+n)/2+1个数 56 return ((double) (findKthNum(A,0,B,0,(m+n)/2) + findKthNum(A,0,B,0,(m+n)/2+1)))/2; 57 } 58 }