Taylor Approximation
According to Taylor Series:

It defines a way to estimate the value of function f, when the variable x has a small change Δx. If we only use the first two items on the right side of the equation, it is called the first order approximation.
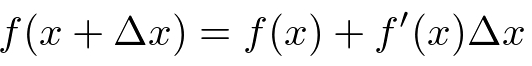
Second-order approximation:
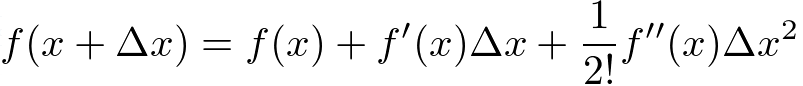
Gradient Descent
When we try to optimize a machine learning problem, actually the target function is the Loss Function L, and at each step if optimization we decrease it by changing the variable θ a little bit. If we put it into the first-order approximation in multivariable case:

Then our expectation is to decrease the Loss by each step of update, so the problem becomes choosing a proper Δθ to guarantee Loss becoming smaller. The way that Gradient Descent used is to take advantage of the Norm. Because a vector's norm is non-negative, we assign Δθ to be the product of a small negtive number α and the norm of the gradient. So
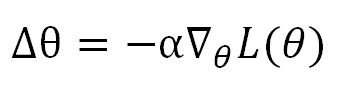
This is the common equation to update θ in Machine Learning course, in which α is the learning rate.