Gaussian Distribution(Normal Distribution)其图形特点为中间高,两头低,是钟形曲线(bell-shaped curve)。在高斯分布中,以数学期望μ表示钟型的中心位置(也即曲线的位置),而标准差(standard deviation)σ表征曲线的离散程度。
随机变量X服从数学期望为μ、方差为σ^2的正态分布,记为:
X = N ( μ, σ^2 )
当数学期望为0,方差为1时,该分布为标准正态分布(standard normal distribution)。
高斯分布的概率密度函数(probability
density function)为:

高斯分布曲线的特征:
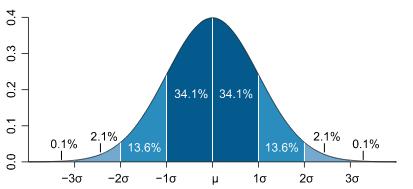
关于μ对称;总面积为1;在μ加减σ处为拐点(先内翻后外翻。
此外,我们通过公式可以看出,σ越大,x位置的概率值就越小,说明曲线越平缓(矮小);而如果σ小,x的概率就大,说明曲线是瘦高的,概率分布比较集中。
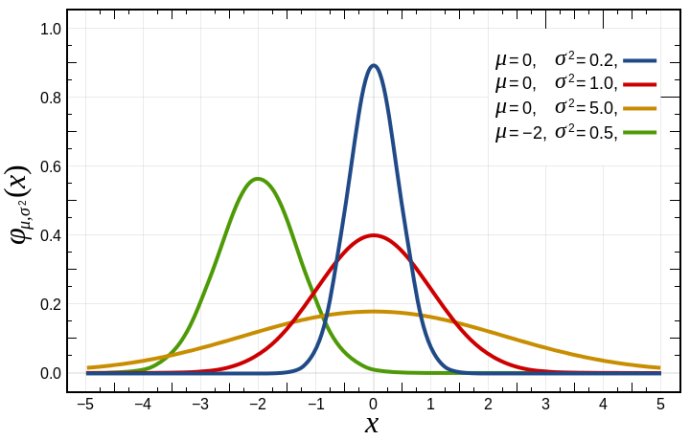
如下图所示,红,蓝,橘黄色曲线的数学期望在0点,但蓝色的方差为0.2,所以其最为陡峭,而橘红色曲线的方差为5.0,证明其分布很广,由于曲线的概率总和为1,所以若其分布广,则高度必然会较低。绿色曲线由于其数学期望为-2,所以,在其他三条曲线的左侧。
 下面,扩展高斯分布到多维:
下面,扩展高斯分布到多维:

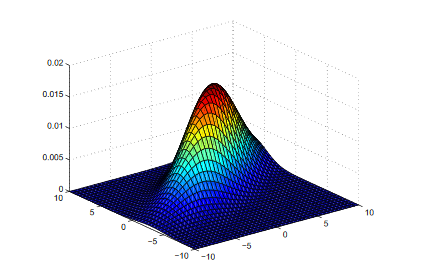
下图是一个二维高斯分布:
https://www.youtube.com/watch?v=JjB58InuTqM