承接上一篇文章对行列式的引入,这篇文章将进一步记录关于行列式的有关内容,包括如下的几个方面:
(1)行列式3个初等变换的证明。
(2)转置行列式与原行列式相等的证明。
(3)定理det(AB) = det(A)det(B)的证明。
(4)基于行列式初等变换的范德蒙德行列式的证明。
首先值得说明的是,先前我们介绍矩阵的时候,并没有给出矩阵行变换的相关证明,其实按道理讲它的根源是出自于这里的。行列式和矩阵是有着紧密的联系的,想在这本书中就是基于矩阵的方法来完成对行列式3个初等变换的证明的。

行列式3个初等变换的证明:
图片中给出的证明过程紧凑间接,无需笔者赘言。在这里之所以采用了基于初等矩阵E的方法,便在于矩阵A与E的乘法运算刚好能够反映这3个初等变换。

转置行列式与原行列式相等的证明:
这个问题其实十分简单,但是我们应该能够意识到这个定理的意义,它使得行变换和列变换具有了等价性,也就是说对行适用的变换方式对列都是适用的。
简略的证明过程:定义行列式A并写出其转置矩阵A^T。
将A行列式按照第i行打开,将A^T行列式按照第i列打开,随后可由转置矩阵的定义,完成证明。
det(AB) = det(A)det(B):

关于这个定理,笔者先前缺少了一些补充知识例如“可逆矩阵的性质”,这是推导过程中|A| = |Ep|…|E2||E1|这一步转化的重要依据。笔者会在抽空将这一转化过程的基本原理。
最后是关于范德蒙德行列式的证明过程。
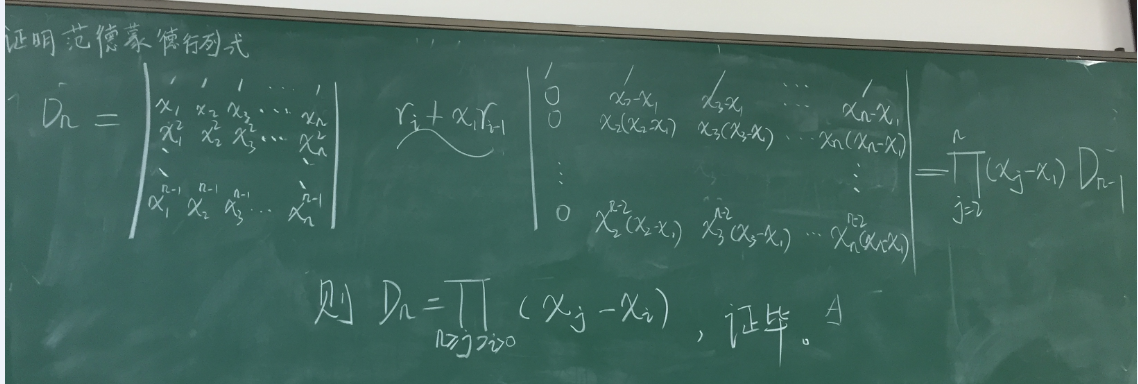
证明过程本身是很简单的,但是它所用到的递归思维是我们在解决其他问题的时候可以借鉴的。