<4>2-D物体间的碰撞响应
这次我要分析两个球体之间的碰撞响应,这样我们就可以结合以前的知识来编写一款最基本的2-D台球游戏了,虽然粗糙了点,但却是个很好的开始,对吗?
一、初步分析
中学时候上物理课能够认真听讲的人应该很熟悉的记得:当两个球体在一个理想环境下相撞之后,它们的总动量保持不变,它们的总机械能也守恒。但这个理想环境是什么样的呢?理想环境会不会影响游戏的真实性?对于前者我们做出在碰撞过程中理想环境的假设:
1)首先我们要排除两个碰撞球相互作用之外的力,也就是假设没有外力作用于碰撞系统。
2)假设碰撞系统与外界没有能量交换。
3)两个球体相互作用的时间极短,且相互作用的内力很大。
有了这样的假设,我们就可以使用动量守恒和动能守恒定律来处理它们之间的速度关系了,因为1)确保没有外力参与,碰撞系统内部动量守恒,我们就可以使用动量守恒定律。2)保证了我们的碰撞系统的总能量不会改变,我们就可以使用动能守恒定律。3)两球发生完全弹性碰撞,不会粘在一起,没有动量、能量损失。
而对于刚才的第二个问题,我的回答是不会,经验告诉我们,理想环境的模拟看起来也是很真实的。除非你是在进行科学研究,否则完全可以这样理想的去模拟。
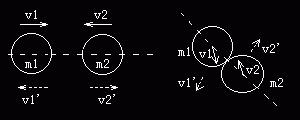
现在,我们可以通过方程来观察碰撞前后两球的速度关系。当两球球心移动方向共线(1-D处理)时的速度,或不共线(2-D处理)时共线方向的速度分量满足:
(1)m1 * v1 + m2 * v2 = m1 * v1' + m2 * v2' (动量守恒定律)
(2)1/2 * m1 * v1^2 + 1/2 * m2 * v2^2 = 1/2 * m1 * v1'^2 + 1/2 * m2 * v2'^2 (动能守恒定律)
这里m1和m2是两球的质量,是给定的,v1和v2是两球的初速度也是我们已知的,v1'和v2'是两球的末速度,是我们要求的。好,现在我们要推导出v1'和v2'的表达式:
由(1),得到v1' = (m1 * v1 + m2 * v2 - m2 * v2') / m1,代入(2),得
1/2 * m1 * v1^2 + 1/2 * m2 * v2^2 = 1/2 * m1 * (m1 * v1 + m2 * v2 - m2 * v2')^2 + 1/2 * m2 * v2'^2
=> v2' = (2 * m2 * v1 + v2 * (m1 - m2)) / (m1 + m2),则
=> v1' = (2 * m1 * v2 + v1 * (m1 - m2)) / (m1 + m2)
我们现在得到的公式可以用于处理当两球球心移动方向共线(1-D处理)时的速度关系,或者不共线(2-D处理)时共线方向的速度分量的关系。不管是前者还是后者,我们都需要把它们的速度分解到同一个轴上才能应用上述公式进行处理。
二、深入分析
首先我要说明一件事情:当两球碰撞时,它们的速度可以分解为球心连线方向的分速度和碰撞点切线方向的分速度。而由于它们之间相互作用的力只是在切点上,也就是球心连线方向上,因此我们只用处理这个方向上的力。而在切线方向上,它们不存在相互作用的力,而且在理想环境下也没有外力,因此这个方向上的力在碰撞前后都不变,因此不处理。好,知道了这件事情之后,我们就知道该如何把两球的速度分解到同一个轴上进行处理。
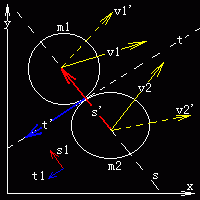
现在看上面的分析图,s和t是我们根据两个相碰球m1和m2的位置建立的辅助轴,我们一会就将把速度投影到它们上面。v1和v2分别是m1和m2的初速度,v1'和v2'是它们碰撞后的末速度,也就是我们要求的。s'是两球球心的位置向量,t'是它的逆时针正交向量。s1是s'的单位向量,t1是t'的单位向量。
我们的思路是这样的:首先我们假设两球已经相碰(在程序中可以通过计算两球球心之间的距离来判断)。接下来我们计算一下s'和t',注意s'和t'的方向正反无所谓(一会将解释),现在设m1球心为(m1x, m1y),m2球心为(m2x, m2y),则s'为(m1x-m2x, m1y-m2y),t'为(m2y-m1y, m1x-m2x)(第一篇的知识)。
则设
sM = sqrt((m1x-m2x)^2+(m1y-m2y)^2),
tM = sqrt((m2y-m1y)^2+(m1x-m2x)^2),有
s1 = ((m1x-m2x)/sM, (m1y-m2y)/sM) = (s1x, s1y)
t1 = ((m2y-m1y)/tM, (m1x-m2x)/tM) = (t1x, t1y)
现在s和t轴的单位向量已经求出了,我们根据向量点乘的几何意义,计算v1和v2在s1和t1方向上的投影值,然后将s轴上投影值代
入公式来计算s方向碰撞后的速度。注意,根据刚才的说明,t方向的速度不计算,因为没有相互作用的力,因此,t方向的分速度不变。所以我们要做的就是:把v1投影到s和t方向上,再把v2投影到s和t方向上,用公式分别计算v1和v2在s方向上的投影的末速度,然后把得到的末速度在和原来v1和v2在t方向上的投影速度再合成,从而算出v1'和v2'。好,我们接着这个思路做下去:
先算v1(v1x, v1y)在s和t轴的投影值,分别设为v1s和v1t:
v1s = v1.s1
=> v1s = v1x * s1x + v1y * s1y
v1t = v1.t1
=> v1t = v1x * t1x + v1y * t1y
再算v2(v2x, v2y)在s和t轴的投影值,分别设为v2s和v2t:
v2s = v2.s1
=> v2s = v2x * s1x + v2y * s1y
v2t = v2.t1
=> v2t = v2x * t1x + v2y * t1y
接下来用公式
v1' = (2 * m1 * v2 + v1 * (m1 - m2)) / (m1 + m2)
v2' = (2 * m2 * v1 + v2 * (m1 - m2)) / (m1 + m2)
计算v1s和v2s的末值v1s'和v2s',重申v1t和v2t不改变:
假设m1 = m2 = 1
v1s' = (2 * 1 * v2s + v1s * (1 - 1)) / (1 + 1)
v2s' = (2 * 1 * v1s + v2s * (1 - 1)) / (1 + 1)
=> v1s' = v2s
=> v2s' = v1s
好,下一步,将v1s'和v1t再合成得到v1',将v2s'和v2t再合成得到v2',我们用向量和来做:
首先求出v1t和v2t在t轴的向量v1t'和v2t'(将数值变为向量)
v1t' = v1t * t1 = (v1t * t1x, v1t * t1y)
v2t' = v2t * t1 = (v2t * t1x, v2t * t1y)
再求出v1s'和v2s'在s轴的向量v1s'和v2s'(将数值变为向量)
v1s'= v1s' * s1 = (v1s' * s1x, v1s' * s1y)
v2s'= v2s' * s1 = (v2s' * s2x, v2s' * s2y)
最后,合成,得
v1' = v1t' + v1s' = (v1t * t1x + v1s' * s1x, v1t * t1y + v1s' * s1y)
v2' = v2t' + v2s' = (v2t * t1x + v2s' * s2x, v2t * t1y + v2s' * s2y)
从而就求出了v1'和v2'。下面解释为什么说s'和t'的方向正反无所谓:不论我们在计算s'时使用m1的球心坐标减去m2的球心坐标还是相反的相减顺序,由于两球的初速度的向量必有一个和s1是夹角大于90度小于270度的,而另外一个与s1的夹角在0度和90度之间或者说在270度到360度之间,则根据向量点积的定义|a|*|b|*cosA,计算的到的两个投影值一个为负另一个为正,也就是说,速度方向相反,这样就可以用上面的公式区求得末速度了。同时,求出的末速度也是方向相反的,从而在转换为v1s'和v2s'时也是正确的方向。同样的,求t'既可以是用s'逆时针90度得到也可以是顺时针90度得到。
三、编写代码
按照惯例,该编写代码了,其实编写的代码和上面的推导过程极为相似。但为了完整,我还是打算写出来。
// 用于球体碰撞响应的函数,其中v1a和v2a为两球的初速度向量,
// v1f和v2f是两球的末速度向量。
// m1和m2是两球的位置向量
// s'的分量为(sx, sy),t'的分量为(tx, ty)
// s1是s的单位向量,分量为(s1x, s1y)
// t1是t的单位向量,分量为(t1x, t1y)
void Ball_Collision(v1a, v2a, &v1f, &v2f, m1, m2){
// 求出s'
double sx = m1.x - m2.x ;
double sy = m1.y - m2.y ;
// 求出s1
double s1x = sx / sqrt(sx*sx + sy*sy) ;
double s1y = sy / sqrt(sx*sx + sy*sy) ;
// 求出t'
double tx = -sy ;
double ty = sx ;
// 求出t1
double t1x = tx / sqrt(tx*tx + ty*ty) ;
double t1y = ty / sqrt(tx*tx + ty*ty) ;
// 求v1a在s1上的投影v1s
double v1s = v1a.x * s1x + v1a.y * s1y ;
// 求v1a在t1上的投影v1t
double v1t = v1a.x * t1x + v1a.y * t1y ;
// 求v2a在s1上的投影v2s
double v2s = v2a.x * s1x + v2a.y * s1y ;
// 求v2a在t1上的投影v2t
double v2t = v2a.x * t1x + v2a.y * t1y ;
// 用公式求出v1sf和v2sf
double v1sf = v2s ;
double v2sf = v1s ;
// 最后一步,注意这里我们简化一下,直接将v1sf,v1t和v2sf,v2t投影到x,y轴上,也就是v1'和v2'在x,y轴上的分量
// 先将v1sf和v1t转化为向量
double nsx = v1sf * s1x ;
double nsy = v1sf * s1y ;
double ntx = v1t * t1x ;
double nty = v1t * t1y ;
// 投影到x轴和y轴
// x轴单位向量为(1,0),y轴为(0,1)
// v1f.x = 1.0 * (nsx * 1.0 + nsy * 0.0) ;
// v1f.y = 1.0 * (nsx * 0.0 + nsy * 1.0) ;
// v1f.x+= 1.0 * (ntx * 1.0 + nty * 0.0) ;
// v1f.y+= 1.0 * (ntx * 0.0 + nty * 1.0) ;
v1f.x = nsx + ntx ;
v1f.y = nsy + nty ;
// 然后将v2sf和v2t转化为向量
nsx = v2sf * s1x ;
nsy = v2sf * s1y ;
ntx = v2t * t1x ;
nty = v2t * t1y ;
// 投影到x轴和y轴
// x轴单位向量为(1,0),y轴为(0,1)
// v2f.x = 1.0 * (nsx * 1.0 + nsy * 0.0) ;
// v2f.y = 1.0 * (nsx * 0.0 + nsy * 1.0) ;
// v2f.x+= 1.0 * (ntx * 1.0 + nty * 0.0) ;
// v2f.y+= 1.0 * (ntx * 0.0 + nty * 1.0) ;
v2f.x = nsx + ntx ;
v2f.y = nsy + nty ;
}// end of function