PRaCtice[1]

ID-3学习 代码实现

该项目采用了业界领先的 TDD（TreeNewBee-Driven Development,吹牛逼导向开发模式） 方式。-Rrrrraulista

目录

• ID-3学习 代码实现
  • 1. 样例数据集
  • 2.信息熵的计算

1. 样例数据集

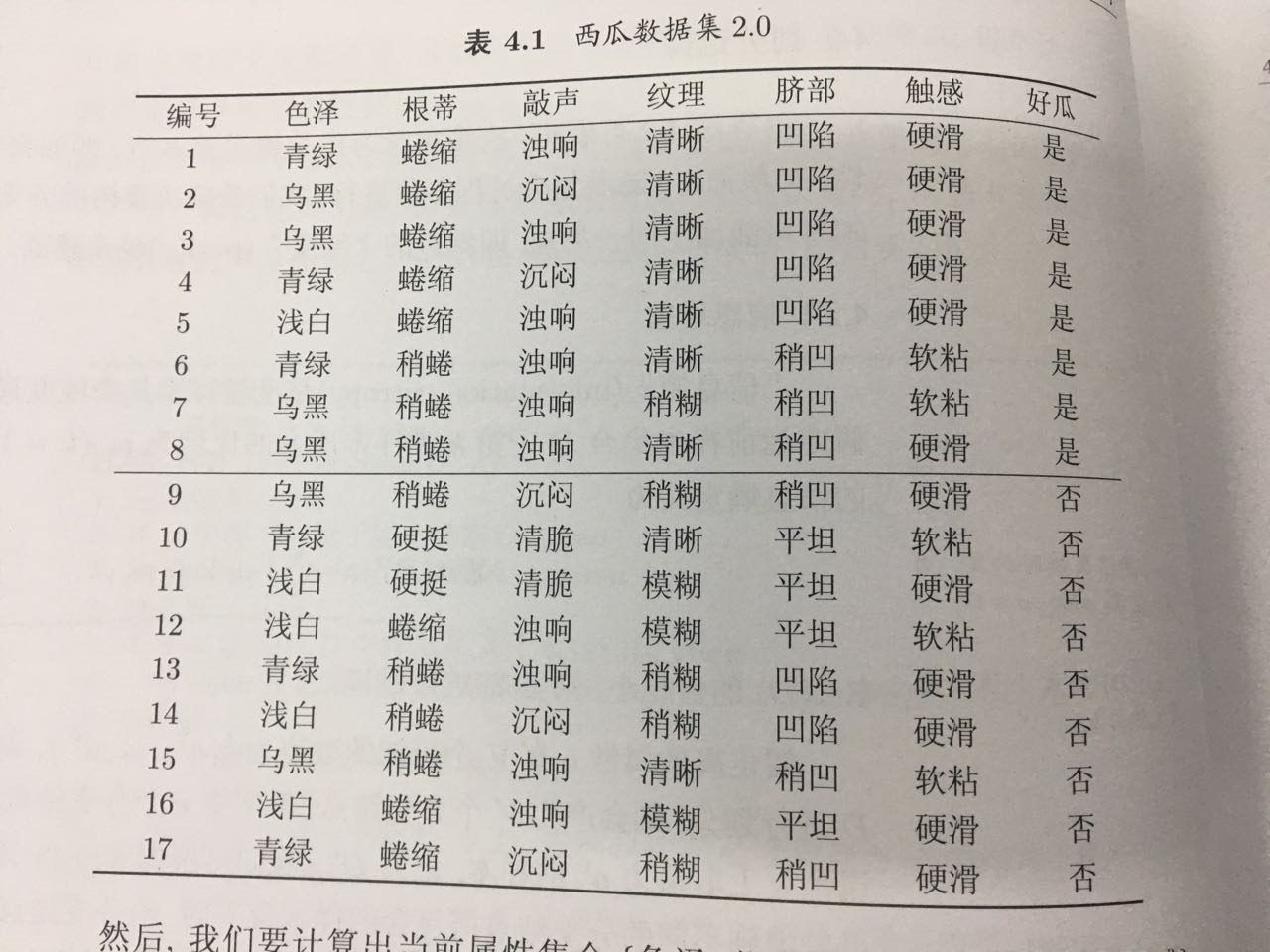
样例数据集来自周老师《机器学习》上的“西瓜数据集2.0”

数据结构定义如下：

结构体类型定义//update

typedef struct SampleNode{
	int SeqNum; 	        //样例编号
	bool Type;			    //样例类别（true 好瓜；false 非好瓜） 

	int Color;				//色泽 	（1 青绿；	2 乌黑；	  3 浅白） 
	int Root;				//根部 	（1 蜷缩；	2 稍微蜷缩；  3 硬挺） 
	int Sounds;				//敲击声音 （1 沉闷；  2 浊响；      3 清脆） 
	int Style;				//纹理 	（1 清晰；	2 稍微模糊；  3 模糊） 
	int Struct;				//脐部特性 （1 凹陷；  2 稍凹；	 3 平坦） 
	int Touch;				//触感 	（1 硬滑；	2 软粘；） 
};
SampleNode sample[17]={ 
	{ 1 , true , 1 , 1 , 2 , 1 , 1 , 1 },
	{ 2 , true , 2 , 1 , 1 , 1 , 1 , 1 },
	{ 3 , true , 2 , 1 , 2 , 1 , 1 , 1 },
	{ 4 , true , 1 , 1 , 1 , 1 , 1 , 1 },
	{ 5 , true , 3 , 1 , 2 , 1 , 1 , 1 },
	{ 6 , true , 1 , 2 , 2 , 1 , 2 , 2 },
	{ 7 , true , 2 , 2 , 2 , 2 , 2 , 2 },
	{ 8 , true , 2 , 2 , 2 , 1 , 2 , 1 },
	{ 9  , false , 2 , 2 , 1 , 2 , 2 , 1},
	{ 10 , false , 1 , 3 , 3 , 1 , 3 , 2},
	{ 11 , false , 3 , 3 , 3 , 3 , 3 , 1},
	{ 12 , false , 3 , 1 , 2 , 3 , 3 , 2},
	{ 13 , false , 1 , 2 , 2 , 2 , 1 , 1},
	{ 14 , false , 3 , 2 , 1 , 2 , 1 , 1},
	{ 15 , false , 2 , 2 , 2 , 1 , 2 , 2},
	{ 16 , false , 3 , 1 , 2 , 3 , 3 , 1},
	{ 17 , false , 1 , 1 , 1 , 2 , 2 , 1},
};

二维数组实现方法

int data[17][7]{//整数类型西瓜数据集二维数组（类别，色泽，根部，声音，纹路，脐部，触感） 
	{1 , 1 , 1 , 2 , 1 , 1 , 1},
	{1 , 2 , 1 , 1 , 1 , 1 , 1},
	{1 , 2 , 1 , 2 , 1 , 1 , 1},
	{1 , 1 , 1 , 1 , 1 , 1 , 1},
	{1 , 3 , 1 , 2 , 1 , 1 , 1},
	{1 , 1 , 2 , 2 , 1 , 2 , 2},
	{1 , 2 , 2 , 2 , 2 , 2 , 2},
	{1 , 2 , 2 , 2 , 1 , 2 , 1},
	{0 , 2 , 2 , 1 , 2 , 2 , 1},
	{0 , 1 , 3 , 3 , 1 , 3 , 2},
	{0 , 3 , 3 , 3 , 3 , 3 , 1},
	{0 , 3 , 1 , 2 , 3 , 3 , 2},
	{0 , 1 , 2 , 2 , 2 , 1 , 1},
	{0 , 3 , 2 , 1 , 2 , 1 , 1},
	{0 , 2 , 2 , 2 , 1 , 2 , 2},
	{0 , 3 , 1 , 2 , 3 , 3 , 1},
	{0 , 1 , 1 , 1 , 2 , 2 , 1},
};

2.信息熵的计算

在二维数组构成的数据集上，先写出对于样本类别的信息熵地计算的基础上，逐步修改，使其具备复用性。

double Entropy(int data[17][7]);	//Declaration of the function
double Entropy(int data[17][7]){	//to calculate the entropy of dataset
	int trueNum=0;	
	for(int i=0;i<17;i++){	//count the number of TRUE numbers, which means 好瓜
		if(data[i][0]==1){
			trueNum++;
		}else{
			continue;
		}
	}
	int  falseNum=17-trueNum;	// Total - true.num = false.num
	double p1=trueNum/17.0;
	double p2=falseNum/17.0;
	if(p1!=0){	//define that 0*log_2(0) = 0
		p1=-1*(p1*(log(p1)/log(2)));
	}
	if(p2!=0){
		p2=-1*(p2*(log(p2)/log(2)));
	}
	double Ent=p1+p2;
	return Ent;
} 
//main（）：double ent=Entropy(data);

可以看到，该段代码成功计算了总体数据集的信息熵约为 0.998（与书上数值相同），但是该段代码默认了数据集长度为17，无法应用于子集合计算，同时传递的参数固定（二维数组），如果不解决该问题，则声明函数无意义，于是下面着手修改，使该函数更加具备复用性。

• 首先为了方便计算数组长度，人为加入数组下界，最后一行所有元素赋值为“-1”

	{-1 ,-1 ,-1 ,-1 ,-1 ,-1 ,-1},

• 这样做能简化程序。

而在此基础上使用如下代码

	int SetLength=0;
	for(int i=0;num[i][0]!=-1;i++){
		SetLength++;
	}

可以实现在函数内计算二维数组的行数，提高了数组的复用性能。

//通过这个函数可以计算出数据集种某个属性具有多少种可能取值
int TypeNum(int set[][7],int att){
	int SetLength=0;			//计算出二维数组行数 
	for(int i=0;set[i][0]!=-1;i++){
		SetLength++;
	}
	printf("
testa=%d",SetLength);	//测试用
	for(int i=0;i<SetLength;i++){
		for(int j=i+1;j<SetLength;j++){
			if(set[i][att]==set[j][att]){
				SetLength--;
				break;
			}
		}
	} 
	printf("
testb=%d",SetLength);	//测试用testb
	return SetLength;
}

//修改后的信息熵计算函数如下所示
double Entropy(int num[][7]){//计算数据关于的类别的信息熵 
	int trueNum=0;
	int SetLength=0;			//计算出了二维数组的行数 
	for(int i=0;num[i][0]!=-1;i++){
		SetLength++;
	}
	for(int i=0;i<SetLength;i++){
		if(num[i][0]==1){
			trueNum++;
		}else{
			continue;
		}
	}
	int  falseNum=SetLength-trueNum;
	double p1=(double)trueNum/SetLength;
	double p2=(double)falseNum/SetLength;
	if(p1!=0){
		p1=-(p1*(log(p1)/log(2)));
	}
	if(p2!=0){
		p2=-(p2*(log(p2)/log(2)));
	}
	double Ent=p1+p2;
	return Ent;
}