https://en.wikipedia.org/wiki/Wavelet
For example, a wavelet could be created to have a frequency of Middle C and a short duration of roughly a 32nd note. If this wavelet were to be convolved with a signal created from the recording of a song, then the resulting signal would be useful for determining when the Middle C note was being played in the song. Mathematically, the wavelet will correlate with the signal if the unknown signal contains information of similar frequency. This concept of correlation is at the core of many practical applications of wavelet theory.
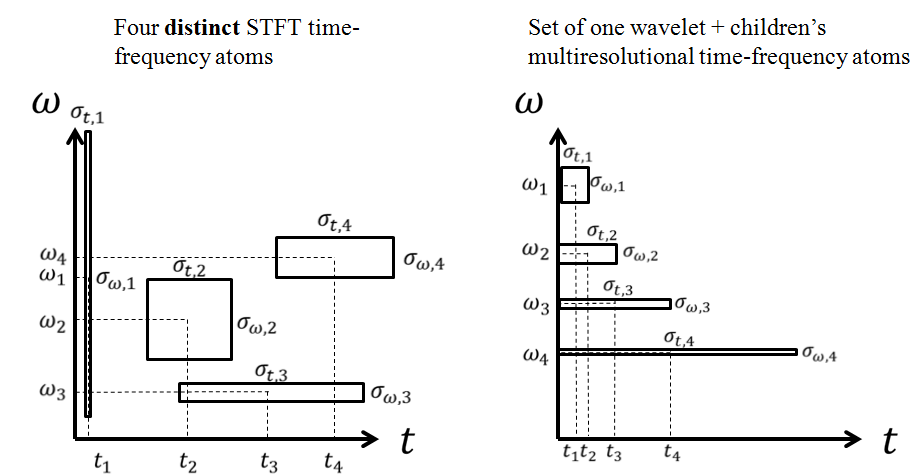
As a mathematical tool, wavelets can be used to extract information from many different kinds of data, including – but certainly not limited to – audio signals and images. Sets of wavelets are generally needed to analyze data fully. A set of "complementary" wavelets will decompose data without gaps or overlap so that the decomposition process is mathematically reversible. Thus, sets of complementary wavelets are useful in wavelet based compression/decompression algorithms where it is desirable to recover the original information with minimal loss.